6 傾度風(けいどふう)
<傾度風>
コリオリの力が働くため、風は等圧線に沿って吹く性質を持っています。等圧線が直線的に引かれる場合には、風は等圧線に完全に沿って吹き、その強さは等圧線間隔に逆比例して、「地衡風」となることは前節で見てきたとおりです。
しかし、等圧線がカーブを描いていると、風は等圧線に沿って吹こうとして、カーブを描きます。
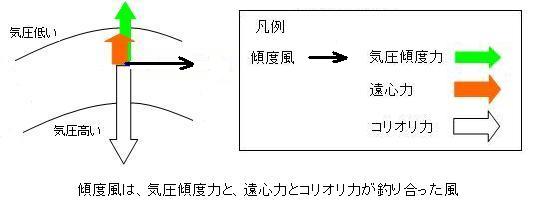
カーブが大きくなると、遠心力が力のバランスに加わってきますので、風を吹かせる力として、「気圧傾度力」、「コリオリ力」及び「遠心力」の3つを考える必要が出てきます。
この3つの力がバランスして吹いている風を「傾度風」と言います。
<高気圧性の風と低気圧性の風>
遠心力は、カーブの方向によって気圧傾度力と反対になったり同じ方向になったりしますので、傾度風の計算を行う前に高気圧性の風、及び低気圧性の風について話しておきます。
これからしばらくは北半球での話とします。すなわち、地衡風に乗って進んでいるとき、進行方向に向かって右側が気圧が高くなっているとします。
したがって、中心付近が気圧の高い高気圧周辺では、風は右カーブを描きながら吹き、逆に中心付近の気圧が低い低気圧周辺では、左カーブを描きながら風が吹いています。右カーブとは上から見たとき、時計の針の進む方向に回転していますので、これを時計方向の回転とも言います。逆方向の左カーブは、反時計方向の回転とも言います。
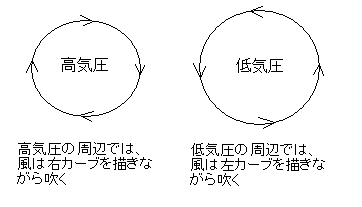
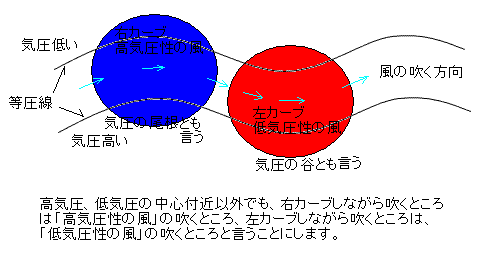
高気圧の中心付近でなくとも右カーブを描いて風が吹くとき、回転の中心方向は気圧が高くなっています。このような場所は「高気圧性の風」の吹くところと言うことにします。このような場所は専門家の中では「気圧の尾根」とも言われます。
逆に低気圧の中心付近でなくとも左カーブを描いて風が吹くとき、回転の中心方向は気圧が低くなっています。このような場所は「低気圧性の風」の吹くところと言うことにします。このような場所は専門家の中では「気圧の谷」とも言われます。
<傾度風の計算>
高気圧周辺や高気圧性の風の吹くところでは、風は右カーブを描きながら吹いており、遠心力は右から左に掛かります。従って気圧傾度力と同じ方向に働くため、この合力とコリオリ力が釣り合う場合にバランスの取れた風、すなわち「傾度風」となります。
一方、低気圧周辺や低気圧性の風の吹くところでは、風は左カーブを描きながら吹いており、遠心力は左から右に掛かります。従って気圧傾度力と反対方向に働くため、気圧傾度力から遠心力を引いた力がコリオリ力と釣り合う場合にバランスの取れた風、すなわち「傾度風」となります。
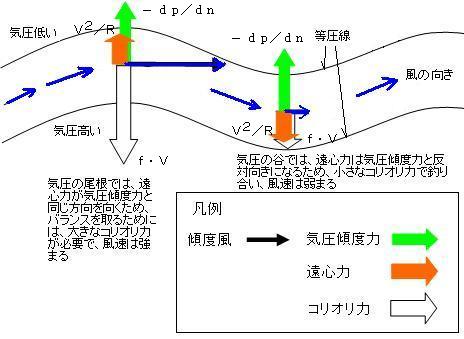
これらのことから、傾度風は気圧の峰では、地衡風より大きく、気圧の谷では、地衡風より小さくなります。実際の例を見てみましょう。 下図は2004年11月29日グリニッジ時刻12時(日本時間29日21時)の高度約12500mの天気図です。
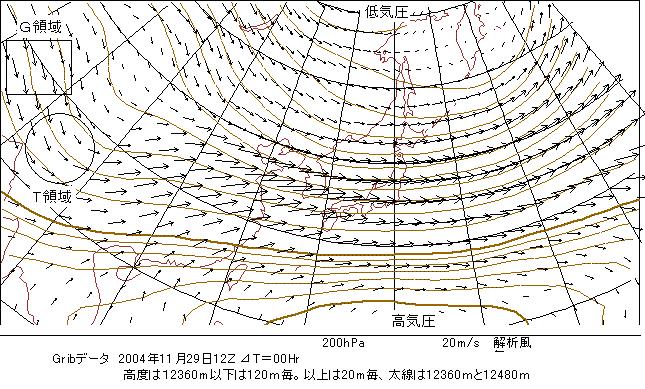
資料は既に地衡風の例の時に申しましたが、気象庁が数値予報を行うときに初めの状態として採用しているもので、等圧面高度(気圧に相当します)と風の分布を示したものです。図の左上の四角い枠で示したG領域は、殆ど直線的でほぼ地衡風と考えられます。その風の流れの先の丸い枠で示したT領域は、左カーブを描いており、反時計方向の回転をしています。ここは気圧の谷になっており、G領域より等圧線間隔が狭くなっているのに、風速は弱くなっていて、これは低気圧性の風の傾度風の特性を示しています。
2本の等圧線に挟まれた間に、例えば1mの深さの空気の流れる量を考えると、地衡風の場合は、その間隔が広くても狭くても同じ量の空気が流れていて、等圧線から溢れたり、外から入って来たりはしなかったのですが、傾度風の場合は、気圧の峰では、多くの空気が流れ、気圧の谷では、少ししか空気が流れなくなりますので、溢れるようなことも起こってきます。このことは後で、述べますが、天気現象にとってに大変重要です。
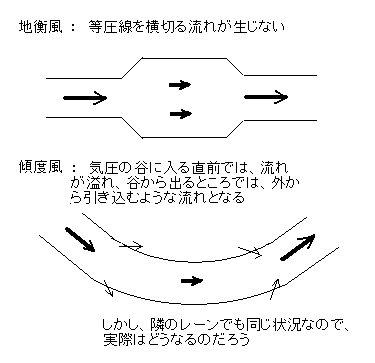
次に傾度風の計算をしてみましょう。

低気圧性の風の場合は、風が正の値を取る条件により、根号の前は、プラスのみを用いることになります。

参考図書
- 小倉義光:「一般気象学」(第2版)、東京大学出版会、p.142-144
↑ 目次へ |