5 地衡風(ちこうふう)
<地衡風を求める式>
風は水平方向の気圧の傾きによって空気の塊が押されて運動するために起こりますが、回転する地球の上では、速度を持った物にはコリオリの力が働いて、常に横方向に力を加えられて、その向きを変えられていきます。
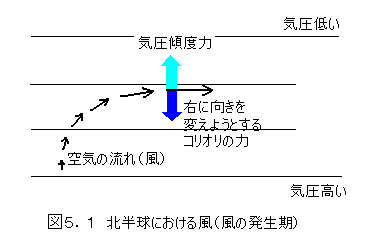
気圧の傾きによって気圧の低い方に流れ出した空気の塊は、北半球ではコリオリの力によって次第に向きを右に向けられ、ついには、等圧線と平行な向きに風が吹き始めます。もしもここで、気圧傾度力とコリオリの力が同じ大きさになれば、気圧傾度力とコリオリ力の向きが正反対ですので、力が釣り合います。力が釣り合うと、この空気の塊に力が全然掛かってないのと同じになり、ニュートンの法則によって、等速直線運動をする事になります。
すなわち、等圧線に平行で、右側に高気圧を見る様な風向で吹き、等圧線の間隔に逆比例する風速になります。
等圧線が緩やかにカーブを描けば、等圧線に沿って風も緩やかにカーブを描いて吹きます。このように気圧傾度の力とコリオリの力が釣り合った状態で吹く風を地衡風(ちこうふう)と言います。現実に1000m位から上の風はこの地衡風になっていることが多いようです。
既に「風は気圧差で起きる」のところでやったように、水平方向に気圧差がある空気は、気圧差(パスカル単位)をその距離(m単位)で割った値がその間にある空気1立方mに与えられる力としてニュートン(N)と言う力の単位で与えられる事が分かっています。
一方、コリオリの力は、その1立方mの大気の質量がρ(Kg)とするとρ・2・ω・sinφ・vで与えられますので、地衡風を求めるための関係式は、

となります。気圧傾度力にマイナスが付くのは、距離が大きく(遠く)なるほど気圧が高くなるとき、手前側(マイナス方向)に力が向くからです。2・ω・sinφを纏めてfと書きコリオリのパラメータと呼びますが、コリオリのパラメータを用いると

これが、いわゆる地衡風の式です。
以上を纏めますと、地衡風は、気圧の高い方を右側に見るように等圧線に沿って吹き、等圧線間隔に逆比例して吹いています。
<実際の風と地衡風>
実際の風がどのように吹いているかの参考資料として、数値予報のイニシャル値の分布を示します。
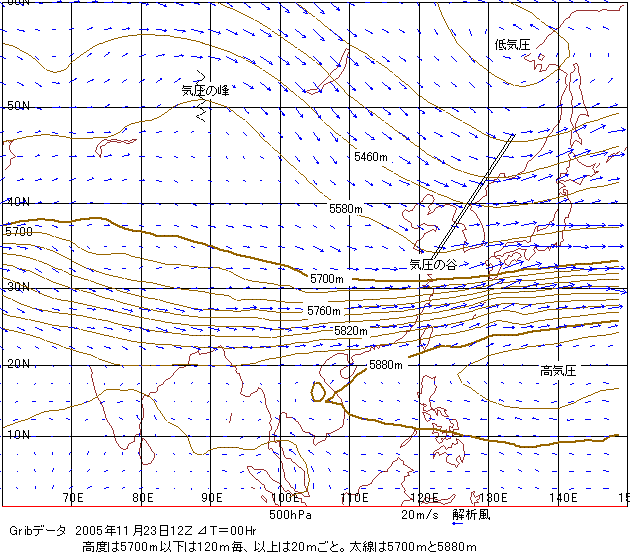
このイニシャル値は、観測資料も参考にして、現在最も観測現況に近いデータと見なすことが出来ます。この初めの状態から流体の運動方程式などを用いて、今後数日間の大気の状態をコンピューターを用いて計算し、予想します。
図は、高度5500m付近の天気図です。図で「高度」と言うのが地上天気図で言う気圧と考えてください。高度の高いところが気圧の高いところで、茶色の実践が等高線(地上天気図の等圧線に相当します)です。上層の天気図の見方については、そのうち一節を設けて説明するつもりです。
青い矢印が沢山示されていますが、その場所の風を示しています。矢印の方向に風が吹いており、風速を矢尻の長さで示しています。矢の長さが倍になれば風速も倍の風速になっています。
風は、殆どのところで、ほぼ等高線に沿って吹いており、高気圧を右側に見るように吹いています。等圧線間隔の広いところは弱く、狭いところは強い風が吹いていることを見てください。
<地衡風の特性>
地衡風は等圧線に平行に吹き、等圧線間隔が倍になると、風速が半分に、間隔が半分になると風速が倍になります。と言うことは、等圧線の間隔が広いところも狭いところも、等圧線の間を流れる風の量は等しく、等圧線を流れの溝の縁と考えると、流れは溝に沿って過不足無く流れ、「発散の無い」流れとなります。
またsinφに逆比例しますから、同じ等圧線間隔では、極に近い方では、地衡風は小さくなります。オホーツク海付近の発達した低気圧の等圧線間隔は非常に狭くなっていますが、西日本付近の等圧線間隔からすると、少し弱い風になっています。北緯60度と北緯30度で同じ等圧線間隔になっていた場合、緯度30度で20m/s吹いていると、同じ間隔では、緯度60度では、11.5m/sになっています。
赤道では、どうでしょうか。sin0=0で分母が0になりますから無限大の風が吹く事になります。実際に気圧差があると、風を止めるのは摩擦だけになります。摩擦があると、地衡風と違って、気圧の高い方から低い方に、等圧線を横切る風が吹きます。ですから、熱帯付近で気圧差があれば、気圧差を直ぐに解消する(気圧の低い方に空気が流れると気圧差が解消します)ように吹きますから、実際の天気図をご覧頂くと分かりますように、熱帯付近では、等圧線が殆ど引かれていません。気圧差が殆どないために等圧線を引くことができないのです。