4 コリオリの力
静止空間を真っ直ぐに進む物が、回転する空間に居る人から見ると、向きを曲げられながら進んで見える事が分かりました。向きを曲げられると言うことは何かの力が進む方向に横から働いていることになりますが、この力のことを初めに気が付いた人の名に因んでコリオリの力と言っています。コリオリの力は、その人のいる場所の水平面の回転速度が分かると計算できますので、その値を求めることにします。
前節で地球の回転速度をωとすると、緯度φにおける水平面がω・sinφで回転していることが分かりました。
コリオリの力を具体的に計算する前に、物理の基礎をおさらいしておきましょう。運動の様子を見るためには、初めに今考えている物が何処にあるか(位置座標)を調べ、次にその位置を単位時間にどのように変化させているかを調べると、これが速度になります。そしてその速度が単位時間にどのように変化しているかを調べると、これが加速度になります。
加速度が分かると、その物体に働いている力が分かります。ニュートンの法則によると、加速度と質量の積はその時に働いている力になりますので、加速度はその物体の単位質量(1Kg)に働く力と見ることが出来ます。
<回転座標で位置ベクトルを書く>
回転軸が垂直な回転座標で位置ベクトルは図4.1の様に示すことが出来ます。このときの回転速度はωであったとします。
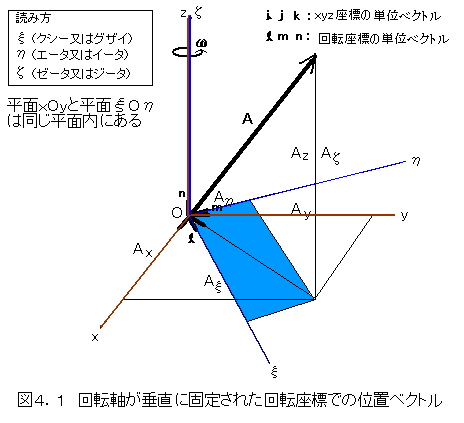
垂直軸上方をζ軸、回転している座標の東方向をξ軸、北側をη軸とし、それぞれの単位ベクトルを
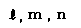
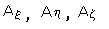
これを式で書くと、位置ベクトルは
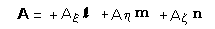
<回転座標で速度を求める>
位置ベクトルAを時間微分すると速度(風速)が得られます。

回転軸が“揺れない”場合の単位ベクトルの時間微分は、
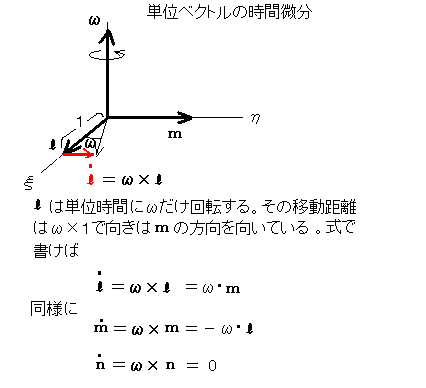
ようになりますので、速度(風速)は、
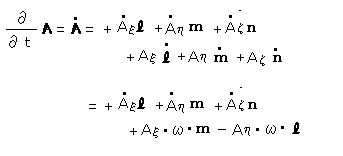
と現すことが出来ます。
<回転座標で加速度を求める>
更にこの速度を時間微分して、加速度
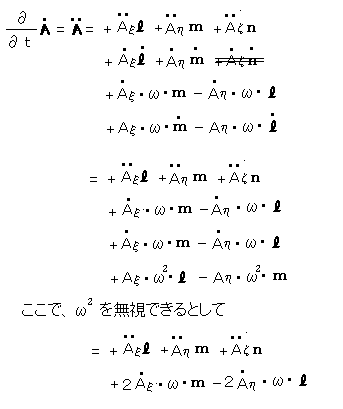
が得られます。
最後の式の1行目は、回転座標系での加速度で、その他に2行目の加速度が加わる事を示しています。2行目の加速度成分を図にしますと、下図の通りです。
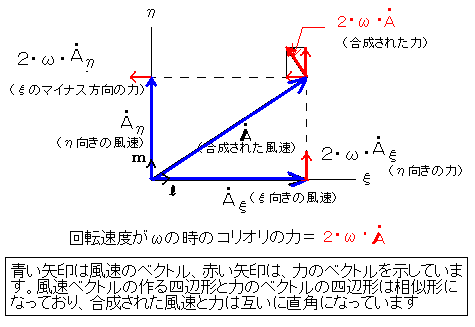
結果は、回転座標系で加速度を取ると、実際の力による加速度の他に、(回転座標系での速度)×(回転速度)の2倍の加速度が運動方向の直角(横向き)方向に掛かる事が分かりました。
したがって、回転速度がω・sinφで回転している緯度φの場所でのコリオリの力は、速度vとすると、2・v・sinφ・ωとなります。
緯度φを北緯がプラス、南緯はマイナスで与えると、この式は南半球にもそのまま、使用することが出来ます。
<コリオリの力の影響>
コリオリの力は、回転する座標系で見た場合の「見かけ上の力」です。見かけというのは、運動の方向を変えることが出来ますが、実質的にエネルギーの変化を起こすことはありません。コリオリの力によって風速が大きくなり運動エネルギーが増加すると言うことはありません。力が働いて、仕事をする場合は、その力の方向にどれだけ移動したかで「仕事」量を現しますが、コリオリの力は、速度に対して常に直角横方向に働いており、いくら働いても、コリオリの力が風速を増加させて、風の運動エネルギーを上げることはありません。このことは、気象を学ぶ上で大きな意味を持たないと思うかも知れませんが、「見かけの力」とは、そういうことです。
コリオリの力は、上で求めたように単位質量に働く力ですので、通常は、単位質量(1Kg)に対して掛かる力で示されます。
質量がM[Kg]のものが速度V[m/s]で飛んでいる場合には、
コリオリ力=2×ω×sinφ×V×M[N]
(Nはニュートンと言う力の単位)となります。
緯度の正弦に比例しますから、高緯度では大きく、低緯度では小さくなります。赤道上では0,すなわちコリオリ力は働きません。
北緯30度の球場で150Km/時の直球を投げると、18.44m先のベースに届くときは0.0014ミリ右にスライドしますが、相手打者の目を混乱させるほどには曲がらないようです。
コリオリの力は、非常に小さいようですが、小さくても長い時間空気を横方向に加速し続けることによって、現実に吹いている風に、大きな影響を与えます。