3 緯度φに居る人の水平面の回転速度
前の節で風は気圧差で起き、気圧の傾きの方向に真っ直ぐ、どんどん加速される話をしました。実際には、地表面との摩擦で一定の速度(風速)で押さえられますが、摩擦を無視できるとしても、風を一定の速度に規制するメカニズムが地球の回転によって与えられている事を、この節と次の節及びその次の節で話したいと思います。
その為には、少し回り道になりますが、回転する地球上から真っ直ぐに飛んでいる物を見るとどのような運動をしているように見えるか、と言う話からさせてください。
例えば、回転する円盤の上にいる人から見ると、まっすぐに飛んでいるボールが、図3.1右図のよう
に曲がって飛んでいるように見えます。非常に大きな回転板上に居る人は、自分が回転していることに気が付かず、あたかも飛んでいる物体は右にカーブしながら飛んでいるように見えます。
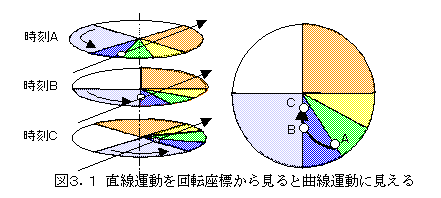
ボールの飛ぶ速さと回転の速さ(回転速度または、角速度と言います。両者の違いはありません)をいろいろ変えて、「曲がり」がどのようになるかを示すと、図3.2
のようになります。円盤は時計の針と反対方向に回っている例で、北半球に居る人の場合に相当します。
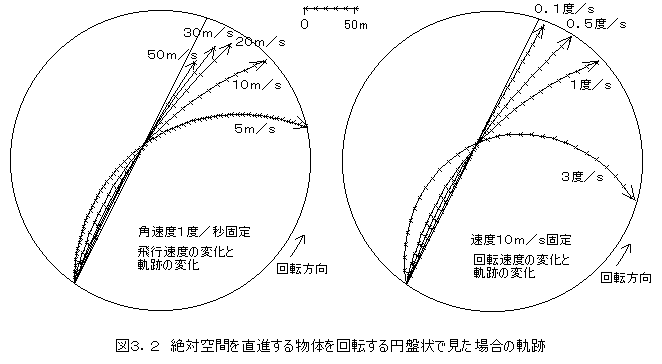
図の左側は、回転板の回転速度は毎秒1度と一定で、物体の飛ぶ速度をいろいろ変えて居ます。それぞれの速度で飛ぶ物体を、円盤上に居る人が見た場合の軌跡を1秒ごとの位置で示しています。
図の右側は、物体の飛ぶ速度を一定速度10m/sとし、円盤の回転速度をいろいろ変えて居ます。こちらも、円盤状に居る人が見た場合の軌跡を1秒ごとの位置で示しています。
図の中央上部に図の距離尺を示していますので参考にしてください。
<地球の回転速度>
図3.2は、理解を易しくするために、回転速度を大きくしましたが、実際の地球の回転速度は非常に小さな値です。だいたいの計算ですが、北極で360度/1日=0.004167度/S(秒をSと表示)程度です。右側の図の0.1度/秒でもかなり直線に近い運動になっていますが、その10分の1以下の回転速度ですので、狭い範囲の現象では、殆ど直線に近い運動に見えるでしょう。
この地球の回転速度約0.004167度/Sを、いちいち書くのがめんどくさいので、よくω(オメガと読みます)で現します。ここでもその習慣に乗ってωで現します。
ここで少しやっかいな問題があります。北極上に住む人は、その人の住む水平面がωの回転速度で回転していることが分かりますが、中緯度、例えば、緯度φの場所に住んでいる人の回転速度はどのようになるか、と言う問題です。
ベクトルに詳しい人は、図3.3の様に地軸の回転ベクトルの緯度成分として理解できるかも知れません。
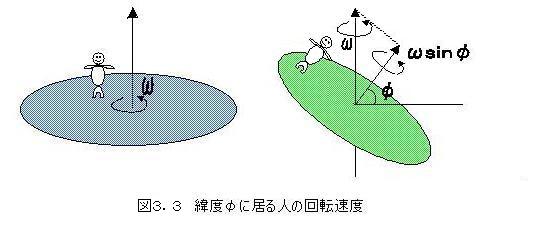
図3.3の説明では良くわからへん方のために、回転速度についておさらいをしてみましょう。
理科や数学では、角度をラジアンで現します。360度が2×π(パイ)ラジアンです。パイは円周率と言い、円周の長さが円の直径の何倍になっているかを現す比率です。3.1415926535・・と延々と続くそうです。この値の正確な値がコンピューターで何桁まで出たとか言うニュースを聞いたことがあるのではないでしょうか。ぐるっと一回りする角度はその円周率の2倍(約6.28)ラジアンになっています。
ラジアンを用いると、回転運動する物体の単位時間の移動距離sが回転半径rと角速度ω(ラジアン/秒)を用いて、s=r×ωで現すことが出来ます。t秒間で移動した距離Sは、S=r×ω×tです。
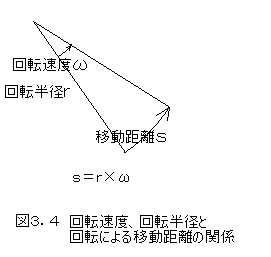
回転運動には周期Tを考えることが出来ますが、単位時間に回る角度ωで1周2×πを割ると周期T=2×π/ωが求められます。回転半径rで回るモノが1周期の間に移動する円周上の距離は、S=r×ω×T=r×ω×(2×π/ω)=2×π×rとなります。丁度円周の長さになります。当たり前の計算のようですが、1周期の間に、円周上を丁度1回りする事を確認しておきました。
正直言うと私も図3.3の説明では良くわからへんのです。自分なりに納得できる理解の仕方を考えました。今、緯度φに居る人の水平面をどんどん広げて考え、地球の回転軸をも含むほどの水平面を考えます。図3.5で緑色の堅い板を緯度φの人の水平面として考えます。
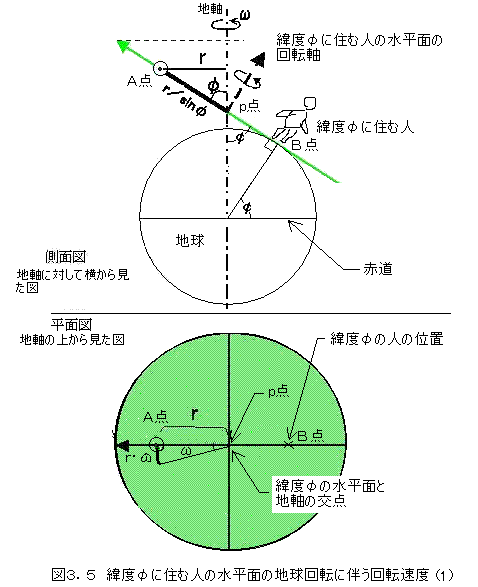
この水平面は地軸と角度φで斜めに固定されて、地軸回りに1秒間にωラジアンで回転しています。緯度φに居る人の位置B点から水平面が地軸と交わる点p点を通る直線上にA点を考えます。 このA点から地軸に垂線を降ろし、垂線までの距離をrとすると、単位時間(1秒間)にr×ωだけ地軸を中心に移動します。
一方、緯度φの水平面に立つ人には、このA点の回転はp点を中心にして、立っている頭の方向(天頂)を回転軸として考えますので、p点を中心に回転している事になります。図3.5を参考に回転軸までの距離はr/sinφとなります。A点の移動は、さきに計算した通りr×ωです。
回転速度=移動距離/回転半径
の関係を用いて回転速度を計算すると、単位時間にr×ωだけ移動し、回転半径がr/sinφですから、この回転速度はr×ω/(r/sinφ)=ω・sinφとなります。
B点とp点を通る直線上のポイントだけで回転速度を求めましたが、p点を通ってBpに直角な直線上のポイントでも、同じ回転速度になることが証明できます。
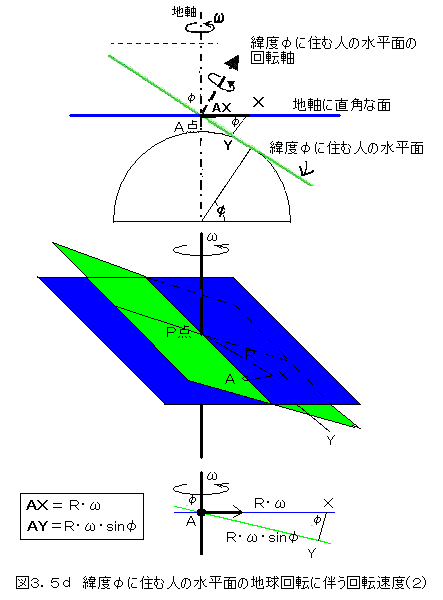
図3.5d で緑色の板が緯度φの水平線、青い板はこの水平面が地軸と交差する点Pを通り、地軸に直角な面です。この緑色の板と青い板の交差する直線上の任意のA点に付いて考えます。A点と地軸との距離をRとすると、このA点は青い板の上を単位時間にω・Rの距離(図3.5dの上の図参照)だけ移動します。この移動は緯度φに住む人の水平面内では、ω・R・sinφ だけの移動距離になります。この移動距離を回転半径Rで割ると、回転速度はω・sinφになります。
水平面は堅い平板と見ることが出来ますので、1点の回転速度が求まれば、この水平面のすべての点がp点を中心に角速度ω・sinφで回転していると言えます。
この計算は任意の緯度の人に成り立ちますので、緯度φの水平面の地球回転に寄る回転速度は、一般的にω・sinφ であると言うことが出来ます。
これまでの説明で、2点疑問点が出てくるかも知れません。一つは、緯度φの水平面がp点を中心にω・sinφで回転していることは分かったが、緯度φの位置での回転速度とは違うのではないか。と言う問題です。
図3.6で説明致します。
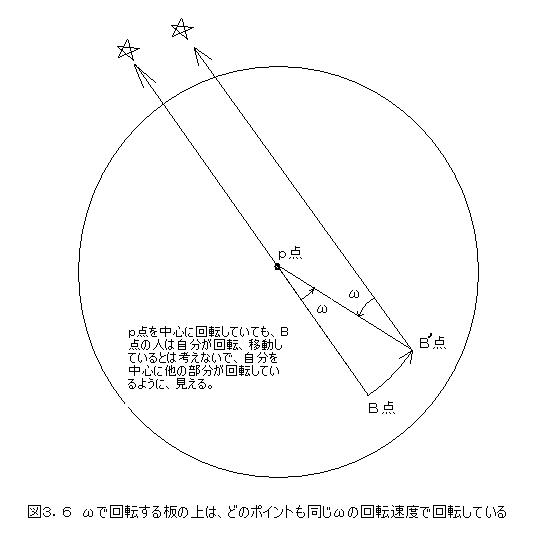
外から見ると、p点を中心に回転速度ωで回転する板があります。この回転板上の任意の点をB点として、このB点上に居る人の立場で考えてみます。B点に居る人は、すべての物を自分の位置から相対的に測りますので、自分の位置が座標の原点です。そして方向を決めるのは、無限に遠いところにある、星の方向などを指標に用います。B点から距離rのp点は、距離rを保ったままで、単位時間にωラジアンだけ反時計方向に回転して見えます。自分がp点の回りを回っているとは感じる必要はありません。自分を中心に回転板が回転していると考えることが出来ます。すなわち、堅い回転板がどこかを中心に回転しているときは、その板上の何処でも、同じ回転速度で回転していると考えることが出来ます。
もう一つの問題は、図3.5の水平面の頭上の方向(天頂)が地軸の回転に寄って変動することの問題です。いわゆるコマの軸が揺れるときにコマの回転を問題にしていることになります。その値は小さいとして無視しています。
<緯度φの回転速度がω・sinφで示される意味>
緯度φの回転速度はω・sinφで示されますが、これは、北極、赤道等の特殊な場所にも、そのまま適用することが出来ます。例えば北極ですと緯度φは90度ですから、sin(90度)は1.0で、北極点上では、地球の回転速度ωそのものになります。
また、赤道上では、sin(0度)は0.0になり赤道上の地平面は回転が無いことになります。回転の無い地平面が地球上に存在することは、後で述べる地衡風(ちこうふう)を考えるときに、問題になってきますので、その時に改めて考えることにしましょう。
回転の方向にプラス、マイナスを考えます。反時計回りをプラス、時計回りをマイナスの回転とする事にすると、そして、北緯をプラス、南緯をマイナスで表現すると、この式は南半球にも適用できます。
北半球で投げた石は右にカーブしながら飛び、赤道で投げた石は真っ直ぐ飛び、南半球で投げた石は、左にカーブしながら飛んでいきます。カーブの強さ?は北半球でも南半球でも極に近いほど大きくなります。
← 風は気圧差で起きる | → コリオリの力 |