9 大気の対流とエマグラム
<エマグラムの見方の前に一言>
天気変化は水分を含んだ空気の上昇や下降で、すなわち空気の対流によって、起こることを第1 節で簡単に述べましたが、上昇や下降によって気圧や気温がどのように変化するのかを詳しく見 ていきます。
そして、空気と一緒に運ばれていく水蒸気は殆ど空気の温度と同じ温度を示すために、上昇と共 に温度が下がり、水蒸気として存在できる量が少なくなって、湿度が100%になり、それでも 尚、上昇していくと余分の水分が雨として落下していくことになりますが、その辺の事もこの節 で話していきたいと思います。
厳密に言うと、湿度が100%になっても直ぐに凝結は始まらないようですが、ここでは原理的 な話として進めていきます。
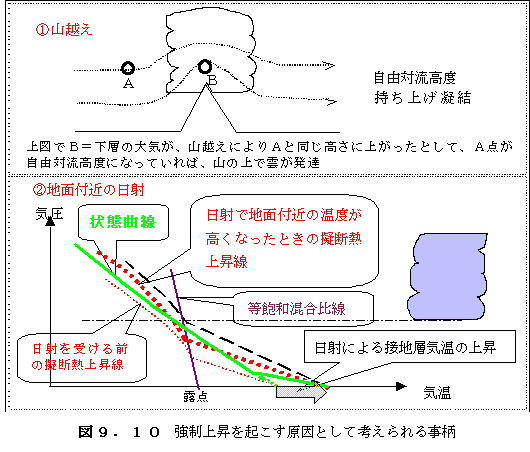
低緯度では、強い太陽の熱エネルギーを受けて、地面が強く熱せられます。熱せられた地面は接 する空気を暖めますので、地面付近の空気は大変温度が高くなります。ある場所の空気の温度が 部分的に高くなると、周囲の空気に比べて軽くなり、浮力ができます。
浮力によって上がり始めると、気圧が下がり気温が下がります。下から上がっていった空気が上 空にあった空気と比べて温度が高ければ、なお浮力を持ち続け、どんどん上昇を続けます。持ち 上げた空気の温度が周囲より低ければ、周囲の空気より重くなり、上昇続けることが出来ません。
空気が上昇するときに気圧が下がり、気温が下がります。これら の計算は結構複雑で、めんどうくさいものです。しかし、その面倒な計算をしてくれて、あらか じめ図に現したものがあります。その意味が分かって居れば、いちいち計算しなくても複雑な変 化を図で見て検討出来るようになっています。その便利なモノは、エマグラムと言います。
初めにエマグラムの考え方を知るために簡単に熱力学の話をし、次にエマグラムの見方の話をし
ます。熱力学をやっている暇は無いよと、言われる方は、エマグラムがこれらの熱力学の式を予
め計算してくれて、図にしたものである事だけを理解して、"エマグラムの見方"に進んで頂いて
も結構です。
<乾燥断熱変化と温位>
理科でボイル・シャルルの法則を習ったことを思い出してください。「気体は一定気圧の元で、
その体積が気温に比例する」と言うのがシャルルの法則、「一定気温の元ではその体積は気圧に
反比例する」と言うのがボイルの法則です。この二つの法則を同時に示したのがボイル・シャル
ルの法則です。気体1Kgの体積をα、気圧をP、絶対温度(摂氏温度に273.15を足した
温度)をTとして、このことを式で書くと、
α=c・T/P(cは比例常数)
と書くことが出来ます。絶対温度の単位は[K]で示します。この式と同じ意味を持つ式で、空
気に当てはめた式を気象学では、状態方程式と言い、
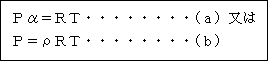
と書きます。また、1Kgの体積αは、比容と呼びます。Rは乾燥空気の気体常数と言い、2 87[m2・s―2・K―1]と決まった値です。ρは空気密度で単位は、[Kg/m3]で す。既に「気圧と等圧面と風」で定性的な話はしましたが、この式は乾燥空気の状態を示すも のです。
3つの状態量、すなわち気圧、気温、と密度又は比容のうち、2つが分かれば残る一つは計算 によって求めることが出来ることを示したものです。
3つの量が互いに関係しあっていますので、例えば、上昇により気圧をΔPだけ変えると、気
温も比容も変化します。気温の変化量をΔT、比容の変化量をΔαとすると、ΔP・α+P・
Δα=R・ΔTの関係式が得られます(状態方程式の微分を取る)。これから
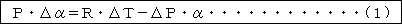
一方、熱力学の第1法則というのがあって、それによると気体に熱エネルギーΔQを加える場合 に、そのエネルギーは、気体の体積を変えないで温度を上昇させるために使われるエネルギーと、 気体の体積を変えることによって他になす仕事量に使われます。式で書くと
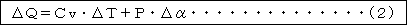
が成り立ちます。ただし、Cvは、定容比熱で体積を変えないようにして温度を一度上げるため に必要なカロリーです。
上の(1)式と(2)式から
ΔQ=Cv・ΔT+R・ΔT-ΔP・α =(Cv+R)・ΔT-ΔP・α となり、Cv+R=Cとすると、この定数Cは、圧力変化ΔPが0の時、ΔQ=C・ΔTとなり、気体を1度高める のに必要なカロリー、すなわち定圧比熱になっています。定圧比熱をCpとすると、
ΔQ=C・ΔT-ΔP・α
となります。
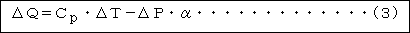
が得られます。 このΔQが0であるような変化は、外部との熱のやりとりの無いことを示し、断熱変化と言われ ます。大気は太陽エネルギーを直接吸収するのがへたですので、通常の大気の変化は断熱変化と してあつかわれます。
ここで少しややこしいかもしれませんが、数学のテクニックを用います。
ΔQ/(T・Cp)がある変数(x)の変化率(Δx/x)になるような変数xを考えると、そ
の変数xは断熱変化(ΔQ=0)に対して不変です。
その関数をx=θとすると、
Δθ/θ=ΔQ/(T・Cp)
=(Cp・ΔT-ΔP・α)/(T・Cp)
=ΔT/T-ΔP・(R・T/P)/(T・Cp)
=ΔT/T-R/Cp・ΔP/P
となり、これを解くと、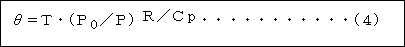
が得られます。このθを「温位」と言います。
温位は断熱変化(ΔQ)に対してその値が変化しないように定義した物理量ですが、これまで 考えてきている空気は乾燥空気ですので、このような式で現される気圧、気温の変化は乾燥断 熱変化と言い、ここで定義した「温位は、乾燥断熱変化に対して、変化しない」と言います。
Pοは特定の気圧の意味ですが、普通1000hPaを用います。
(4)式からθの意味を考えてみましょう。PがPο(1000hPa)であるとき、θ=T ・(Pο/Pο)^(R/Cp)=T・1^(R/Cp)=Tですから、「温 位」θとは、1000hPaの温度であったことが分かります。(^はベキ乗を示す)
(4)式の対数を取ると、
logθ=log(T・(Pο/P)R/Cp) =logT+R/Cp・(log(Pο)-log(P))となります。Pの項を左辺に移動すると、
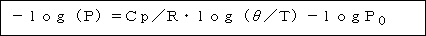
が得られます。この式は1000hPaでθの温度を持つ乾燥空気が、断熱変化をするときの 気圧と気温の関係を示しています。
乾燥空気の状態は気圧と気温が分かればその特性が分かりますから、縦に気圧、横に気温を描 いたグラフを考えると、今考えている空気の特性はグラフ上の位置で示すことが出来ます。し かも気圧を縦座標にしたグラフは、気圧の低い方を上に示すと、縦軸を高度と同じものとして捉 えることができます。
このようなグラフ上に、温位θの値を適当に決め、気圧を、例えば1000hPaから、1h Paずつ下げていくと、それぞれに対応した気温が得られ、これらの点を連ねて描きますと、 温位θの空気が上昇するときの温度変化が図に示されたことになります。
これらの点の連なりを、縦座標を気圧の対数値で、上ほど小さくとり、気温を横座標で右に気
温が高くなるように取ると、殆ど直線に近い線に描くことができます。このようなグラフ上に
温位が270度K、280度K、290度K、と10度K毎の線をあらかじめ描いておくと、
その間の温位の空気に対しても、乾燥空気が上昇するときの気温変化が示されます。
<乾燥断熱変化>
エマグラムは、Energy per unit mass diagram の意味です。 これまで述べてきた熱力学の法則に従うと、乾燥空気が上昇するにつれて、どのように気圧変 化し、それに伴ってどのように気温変化をするかが分かります。
縦軸に気圧(上ほど低い対数 スケール)、横軸に気温を取ったグラフに、種々の温位(1000hPaに強制的に持ってきた時 のその大気の温度を温位と言います)の空気がどのような変化を示すかを予め計算して、図9. 1に示すようにグラフに示しておくと、任意の温位の空気に対してどの気圧まで上がると気温が 何度になるか計算しなくても分かります。
図9.1には、温位が210°Kから450°Kまで10度毎の温位について示しました。°Kは
絶対温度と呼ばれれ、摂氏に273.15を加えた温度の単位です。<ドケイ>と呼びます。温度は、分
子の活動度を示していると見ることが出来、絶対温度の0°Kは、分子の活動が止まってしまった
状態と考えることが出来ると思います。ですから絶対温度のマイナスはありません。
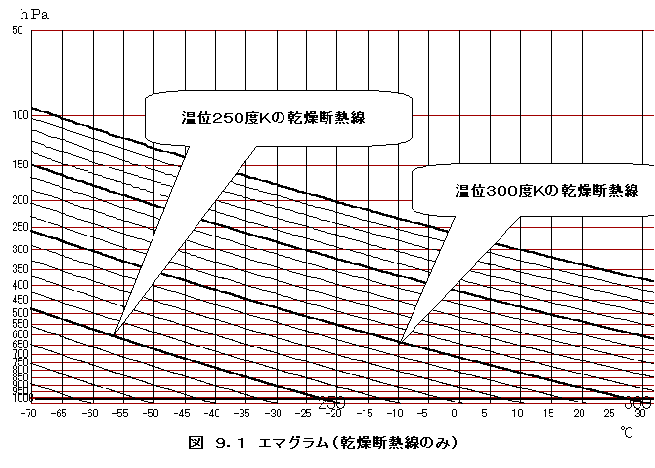
気象的には、気圧は高度を意味しています。図9.1で縦軸の値は、気圧を示していますが、上 ほど高い高度の座標と見て頂いて結構です。横軸の値は、気温を示します。グラムには摂氏で温 度を表示していますが、計算の時には、絶対温度で計算し、表示では使い慣れた摂氏に変えてい ます。温位の単位も温度ですが、温位は、慣例により絶対温度[°K]で示しています。
乾燥断熱線が1000hPaを通るときの温度に273.15を足すと、温位になっていることを確 かめておいてください。
乾燥断熱的に変化させるとは、水蒸気が凝結しない状態での変化を意味し、具体的には雲が発生
しない状態で上昇させることを意味しています。雲が発生しない状態で上昇すると気温が大きく
下がります。例えば、温位300度Kの線を見ますと、地上で気温は約28℃、5500m付近
と言われる500hPaでは約-27℃になっています。5.5Kmで55℃も下がっています。1
Kmで約10℃も気温が下がってしまいます。
<状態曲線>
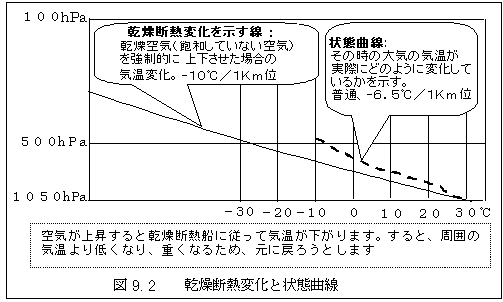
実際に観測される気温変化をエマグラム状に描いたものを状態曲線と言っています。実際の大 気状態を観測しますと、普通1Km上がる毎に気温は6.5℃位低くなっているだけです。
ですから、乾燥した空気を上昇させようとしても、上昇させた空気の気温が周囲の空気の気温よりも
直ぐに低くなり、従って重くなるために、元の位置に戻ろうとします。乾燥した空気は、なかな
か簡単には上昇させることは出来なくなっています。
<飽和混合比>
しかし、水蒸気が入って来ると、水蒸気が凝結して潜熱の放出をし、気温の下がり方が大分少な
くなって、上昇が起こりやすくなります。水蒸気の役割が大変大きいことを見ていきましょう。
空気中には水蒸気が混在し、これが凝結し、雲や雨、雪などに変化することによって複雑な天気 変化を起こしています。したがって気象を知るためには、水蒸気の知識が必要です。
水は100℃以下の常温でも、部分的に空中に飛び出して、気体として飛び交うこともできます。
但し、無制限に多くは混在できません。温度によって水蒸気が存在できる量が決まっています。
温度が高いほど多くの水蒸気が空中に存在できます。ある温度に対して、これ以上水蒸気を多く
含むことが出来ない状態を飽和と言い、乾燥空気1Kgに対して何g含むことが出来るかを示
した数字が飽和混合比です。飽和混合比は気温、気圧によって決まり、図9.3の様に、エマグ
ラムに示されています。
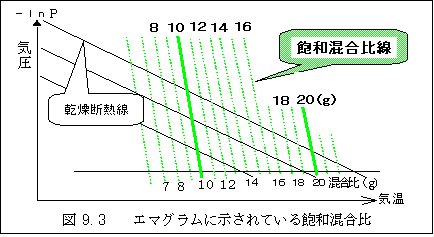
通常は、飽和になって居ることは少なく、未飽和の状態です。その時に乾燥空気1Kgに対して、 水蒸気が何g混在しているかを示す数字が混合比で、混合比とその時の温度と気圧で決まる飽和 混合比との比を取ると、これは相対湿度になります。
図9.4を見てください。初めA(気圧P1、気温T1)にあった空気が乾燥空気1Kgに対し て水蒸気が10gあったとします。すなわちその時の混合比は10gであった事になります。一 方、飽和混合比は気圧と気温によって決まりますが、エマグラムから読みとることができ、気圧 P1、気温T1に対して飽和混合比の値を19gと読むことが出来ます。
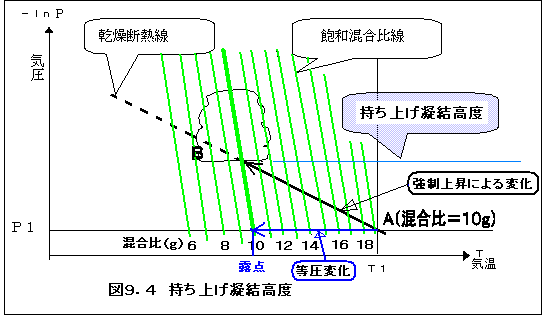
<露点>
気象学では、湿度を現す量として露点と言う量が用いられますが、露点とは、気圧をそのまま変 えないで気温を下げていったときに結露が始める温度の事を言います。
今の場合は、A点から気圧を変えないと言う事ですので、気圧P1の線を横に進み、左に移動す
ると気温を下げることになり、飽和混合比10gと交わった点で、飽和しますので、ここで、結
露が始まります。この点の温度を読むと、これが「露点」になります。
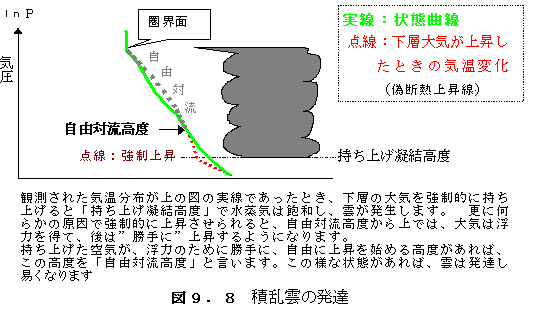
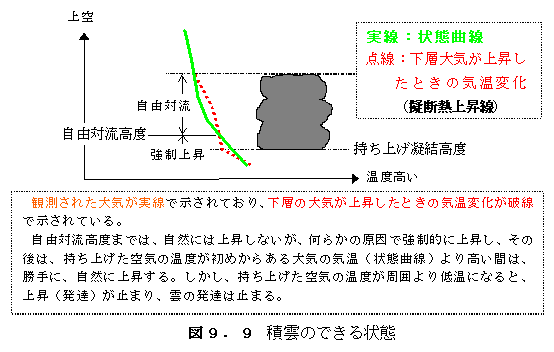
<持ち上げ凝結高度>
A点にあった時の相対湿度は、10/19×100≒53%でした。この飽和していない空 気を強制的に上昇させると、乾燥断熱線に沿って気温が下がり、次第に飽和混合比の値が下がっ てきます。
図では太い実線が、上昇とともに気温の下がることを示し、緑色の線で示した等飽和混合比線を横切 る毎に飽和混合比の値が1gずつ下がっていることを示しています。中に含まれた水蒸気10gは 変化しませんから、混合比10gは変わりません。
A点にあった空気が強制上昇で、乾燥断熱線に沿って上昇し、飽和混合比10gの線と交わった 点Bでは、空気が飽和するため、この高度から霧が出来たり、雲が出来たりします。この高度を 「持ち上げ凝結高度」と言います。
持ち上げ凝結高度は初めに持っている混合比が飽和混合比に近いほど、すなわち湿度(=混合比
/飽和混合比)が高いほど低い高度になります。
<湿潤断熱変化>
雲が発生するまでは、乾燥断熱変化ですが、これから後は湿度は100%で凝結熱を出しながら の変化ですので、湿潤変化になります。水蒸気が凝結をすると、太陽光線からエネルギー吸収が 少しはありますが、ここでは、外部との熱のやり取りは行わないものとし、水蒸気の潜熱のみに ついて考えます。このような変化を湿潤断熱変化と言います。
凝結高度を超えて更に上昇を続けると、飽和混合比はどんどん下がって行きます。乾燥空気1K g当たり10gの水蒸気が含まれているのに、飽和水蒸気が9gになりますと、余分な1gの水 蒸気は凝結して、いわゆる凝結熱を周囲に出すことになります。1gの水蒸気が凝結すると2、 500ジュールの熱を出します。
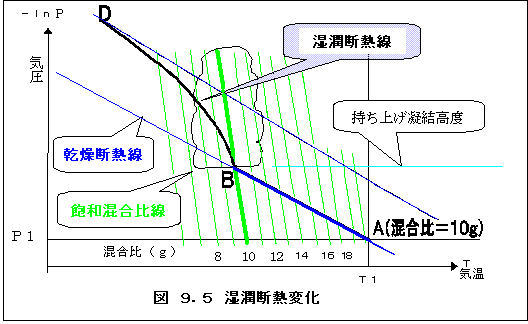
乾燥断熱変化に比べてこの凝結熱の放出分だけ気温の下がり方が少ない変化をするのが、湿潤断
熱変化です。湿潤になった空気の上昇と気温変化の割合も計算によって予め求めることができ、
湿潤断熱線としてエマグラムの中に描かれています。
<相当温位>
持ち上げ凝結高度になった後も、どんどん上昇を続けると、凝結する量は水蒸気が次第に少なく なるため、エマグラムに描かれている飽和混合比線の1g毎の間隔は、その値が小さくなると開いて 行きます。放出する凝結熱も少なくなり、気圧変化に対する気温変化は次第に乾燥断熱線に漸近 します。
湿潤断熱変化を示す線が乾燥断熱線にほぼ平行になった所で、"ほぼ完全"に水分が無くなったと 考えます。すなわち、はじめに空気中に持っていた水蒸気の潜熱を空気中にほぼ全て吐き出させ た事になります。その後この空気を下降させますと、この時の変化は乾燥断熱変化をします。1 000hPaにおける気温、すなわち温位を調べると、初めに持っていた温位に比べて大きな値 になっています。
図9.5で、任意(A点)の大気を、強制的に上昇させますと、凝結高度(B点)までは乾燥断 熱変化で変化し、そこからは水滴を絞り出しながら湿潤断熱変化で変化します。十分水滴を吐き 出した(D点)後、その大気を1000hPaまで引き下ろした時の温度がθeであったとすると、 その(元の)大気の相当温位はθeであると言います。即ち「相当温位」とは、含まれる水蒸気の潜熱 も考慮して基準の気圧(1000hPa)に持ってきたときの(絶対)温度と言うことが出来ます。
単なる「温位」は、乾燥断熱的に1000hPaまで持ってきたときの(絶対)温度と言うことが出来ます。 ある層の大気を強制的に引きずりおろすと、初め湿っていた大気(水滴が無いとして)もすぐに 飽和状態で無くなりますので、乾燥断熱線に沿った変化となります。単に「温位」と言った場合は含 んでいる水蒸気の量を考慮することなく、気圧と気温だけで決定されます。
くどいようですが、相当温位とは、含んでいる水蒸気の潜熱を全部吐き出させて潜熱を全部吐き出させますの
で、相当温位を求めるためには、気圧と気温の他に、その時に含まれている水蒸気量として混合
比(又は、相対湿度でも良い)も必要になります。
<気圧変化に対する温位と相当温位の変化>
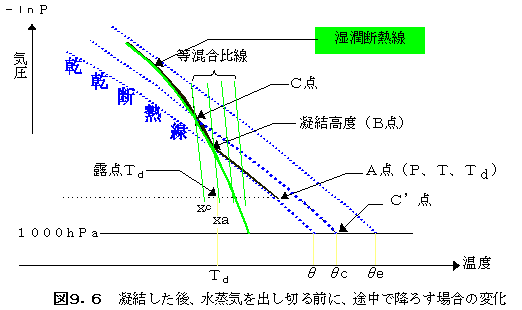
温位をより理解するために、凝結高度から湿潤断熱線に沿って少し上昇し、全ての水蒸気を吐き
出す前に、図9.6のC点から大気を降ろしてしまった場合の温位の変化をθとθeについて考え
て見ましょう。
この様な状況は、山越え気流によるフェーン現象を考えるときに現実に起こります。山をはい上 がる間は、大気の安定度に関係なく強制上昇しますが、山を越えるとその高度から今度は強制的 な下降が始まります。
初めの位置(A点)から凝結高度(B点)までの変化は乾燥断熱で、温位が一定です。
B点から湿潤断熱線に沿う変化をする場合は、乾燥断熱線を横切って(温位の高い方に)移動し ています。乾燥断熱線は等温位線になっていますから、これを横切ることは温位の変化を示し、 この場合温位は高くなっています。
C点で強制的に降ろす事にすると(上昇中にできた水滴は、瞬間に雨として落下させて考えます) その瞬間から乾燥大気として扱うことになりますので、下降する場合は、C点を通る乾燥断熱線 に沿って変化し、C'点に至ります。この時の温度から温位は、θcとなっていることが分かりま す。(θ<θc<θe)
温位を見るために1000hPaまで降ろして見たわけですが、このC'点の大気の相当温位はい
くらでしょうか。ちなみに考え初めにA点にあったときの相当温位はθeでした。
C'点をスタートに相当温位を求めてみましょう。A点をスタートしたときは混合比はXaでした が、B点から結露した水を落として、C点では混合比はXcに減っていました。C点から強制的 に1000hPaまで引き下ろした場合のエマグラム上の点をC'とし、C点からC'点までの往 復の間の変化を考えますと、この間は乾燥断熱変化をしていますので、温位は変わらず、混合比 も変化していません。C点に戻って初めて飽和し、C点から上昇を始めると、湿潤断熱線に沿っ て上昇を始めます。水分を全部落とした後、乾燥断熱線に沿って1000hPaまで降ろすと、 これが相当温位で、その値はθeでA点からスタートした時と相当温位は変化していません。
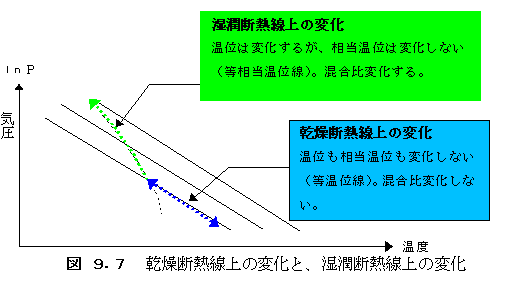
以上見てきたように、大気は上下動をすると気圧が変化し、気圧の変化は気温変化を起こします。 相対湿度が、100%になるまでは、乾燥断熱変化をし、エマグラム上では、乾燥断熱線に沿っ た変化をします。乾燥断熱線は等温位線になっていますので、乾燥した状態での変化では、温位 は変化がありません。また、含まれる水蒸気の乾燥空気に対する比率は、変化がありませんから、 混合比も変わりません。ただし、気温は上昇と共に下がっていきますので、含みうる水蒸気量 (飽和混合比)はどんどん小さくなります。
相対湿度が100%になると湿潤断熱変化をし、エマグラム上では、湿潤断熱線に沿った変化を します。
湿潤断熱線は乾燥断熱線を横切っており、上昇と共に温位の高い方に変化しています。これは、 水蒸気が凝結して潜熱を大気に放出し温位を高めていることを示したものです。大気が含んでい た水蒸気をキリや雨滴や氷晶など気体以外の形に変化させ、考えている大気の外に出すことにし ます。このような変化を、完全な断熱過程では無いので、偽断熱変化と言います。
相当温位は、空気が含んでいる全ての水蒸気の潜熱を吐き出して、基準気圧まで降ろした時の温
度ですから、この湿潤断熱線上の移動においても変化はしません。
<エマグラムのまとめ>
- エマグラムは、縦座標に気圧pの対数(上が小さい)、横座標に気温T(右が高い)を示す 図である。従ってエマグラムの一点が決まれば気圧pと気温Tが決まり、逆に気圧pと気温Tが 決まればエマグラム上のポイントが決まる。
- この図に気圧pと気温Tとで決まる飽和混合比xsが示されている。気圧が決まって、 温度が決まると、その空気が飽和するためにはいくらの混合比(xs)が必要か分かる。
- 露点とは、今の気圧のままで、気温を下げていった時に飽和に達する気温(Td)を言う。 従って、気圧pで、露点Tdの大気の混合比xは、気圧pで、気温Tdの飽和混合比と等しい。 このようにして、気圧pと露点Tdからエマグラムにより、この大気のもつ混合比xが読みとれる。 天気図には「露点差」と言う量が示されていることが多く、これは、気温と露点との差である。 「露点差」から「露点」、更に「混合比」が求められる。
- エマグラムには、縦座標である気圧線、横座標である気温線、および飽和混合比線の他 に乾燥断熱線と湿潤断熱線が引かれている。
- 空気が上昇するとき、飽和するまでは乾燥空気として、乾燥断熱線に沿って気圧や温度 が変化する。この変化の間、混合比、温位、相当温位は変化しない。
- 空気を強制的に持ち上げると、乾燥断熱線に沿って気温は下がり、次第に飽和混合比は小さくな って、ついにはこの空気が持っている混合比が飽和混合比に等しくなる。即ちこの高度で結露が始ま るので、この高度を「持ち上げ凝結高度」と言う。
- 持ち上げ凝結高度よりも更に強制的に空気を上昇させると、飽和混合比が混合比より小 さくなって、余分な水蒸気が凝結し、凝結熱を出すため、気温の低減率の小さい湿潤断熱線に沿 った変化をするようになる。湿潤断熱変化の間は、混合比は飽和混合比と共に小さくなっていき、 温位は大きくなるが、相当温位は、変化しない。