8 高層天気図と風
風の吹き方で上昇気流が起こったり、下降気流が起こったりすることを少し述べてきました。この 後、もっと詳しく話をしていきたいと思いますが、天気変化は、立体的な気流の問題を扱いますか ら、上層の天気図を見る必要があります。上層の天気図を普通、高層天気図と言ってい ます。すこし、専門的に天気図を見るために、どうしても高層天気図の見方の話をする必要があり ます。
高層天気図は、普通、等圧面天気図(とうあつめん天気図)と言う天気図で示しますが、その見方
を説明するために、既に述べてきている部分と重複するかも知れませんが、あらためて気圧の話から
していきたいと思います。
<重さと圧力>
地球上にある物は、全て地球の引力に引っ張られ、重さを持っています。形の固定された固体の場合
は、一つの塊として地球の中心方向(下向き)に、その重心(1点)に掛かる力として扱うことがで
きます。
しかし、気体は自由に飛び交う気体分子からできていますから、一つの塊として扱うことができませ ん。その”重さ”は、飛び交う分子が壁などに当るときに与える衝突の力として、面に力を伝えます。 従って1点だけに集中した力ではなく、単位面積(1m2)にどれだけの力(N;ニュートンと言う 力の単位)を与えるか、と言う計り方をします。この様に面積当たりに与えられる力を圧力(Pa; パスカルと言う単位)と言い、空気の圧力を気圧と言います。普通、気圧は、100パスカルを1単 位にしたhPa(ヘクトパスカルと読む。ヘクトは100の意味。)単位で示します。
1Kgの物は、約10ニュートンの力で地球に引かれています。興味のある人は、ペットボトル
の水を手に持って、力の単位、ニュートンを実感してみてください。
<パスカルの原理>
また、無数の空気分子は完全剛体の球体と考えて良く、互いの衝突によって、その運動方向は全くラ
ンダムな動きをしていると考えられます。従って重力による加速の効果は、下向きに働くだけでなく、
あらゆる方向に同じ強さの衝突を与えます。横、縦、斜め、どの方向でも同じ圧力が与えられます。
これをパスカルの原理と習ったと思います。
<静水圧の式>
とは言いながら、空気という気体も"もの"ですから地球の引力に引っ張られ、重さを持っています。
自由に飛び交っている一つ一つの分子に地球の重力が掛かり、下向きの加速度を得ますので、全くで
たらめに飛び交ってはいますが、下の方の分子は上にある分子より少し速度が大きくなっています。
従って、下にある空気の圧力は、上にある空気の圧力より、少し大きくなっています。
その大きさは、丁度その上に乗っている空気の重さに相当しています。もう少し正確に言うと、水平
に単位面積をとり、上の高さと下の高さの差を⊿h(m)とし、空気密度をρ(Kg/立方m)、重
力の加速度をgとすると、2つの高さの間の気圧の差は、ρ×g×⊿h(パスカル)となります。
<大気圧>
空気の高さは1万m以上にも及びますが、その重さはどれくらいか量ってみますと、地上では平均
的に見て1013hPaくらです。
1013hPaは、1013×100Paで、これは、1平方mに101300ニュートンの力が掛 かっている事を示しています。100Kgの人の重さが約1000ニュートンです。1気圧とは、 1m2の板の上に100Kgの体重の人が101人乗った時の圧力に大体相当します。ドラム缶の 中の空気を抜くとドラム缶がつぶれる実験をテレビでやっているのを見たことがあります。空気の 重さってすごい、ですね。
このすごい圧力というのも、大気が非常に沢山"上"に乗っているからです。上空に行けば"その上に
は1hPa分の空気しか乗っていない高度"、すなわち1hPaの気圧の高度もあります。同じ1h
Paの気圧を示すところは、水平方向に広がっています。
<等圧面>
このような同じ気圧を示すポイントは”なだらかな平曲面”になっていると考えられ、同じ気圧を
示すこの平曲面を等圧面と言っています。
1hPaの等圧面の上には、1hPa分の空気が乗っかって居ます。その下には2hPa、3hPa、 と1hPa毎の気圧面を考えることができ、地上までには約1013枚の気圧面が大気中に広がって いるとます。念を押しておきますが、実際にそんな幕面が存在することはありませんが、頭の中で等 圧面をイメージしておくと大気の理解がし易いと思います。この1hPa毎の等圧面を「hPa等圧 面」と呼ぶことにしましょう。この呼び方は、一般的ではありませんのでご注意下さい。
地上付近のhPa等圧面の差は、高度にして10m弱です。上空に行くと、1hPa間の層の間隔は
少しずつ広くなって行きます。上空2000~3000m位でほぼ10m、1万m位でほぼ20m、
1万5000mでは、1hPaの間隔は50m位になります。
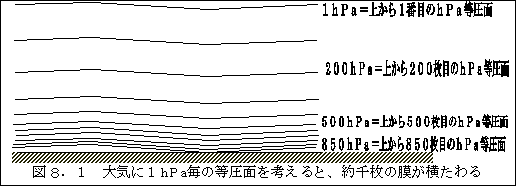
一番上のhPa面である1hPaは4万5000mから5万mの間にあります。上から200枚目が 200hPa面ですが、この200hPa面はほぼ1万2000m位の高さにあり、これ位から下の 大気が上下運動をして天気変化を起こしています。この大気の上下運動を対流と呼び、対流を起こす 大気の層を対流圏と読んでいます。その上の層は上下運動を殆どしない安定な状態になっていて、所 謂成層圏と呼ばれています。対流圏と成層圏の間の面を(対流)圏界面といいます。
200hPaの等圧面に関する天気図がこの後、多く出てきます。これ
からの話は、その200hPa天気図を見ていただくための準備になります。しばらくお付き合い下さい。
<空気が暖められ気圧勾配ができる>
気圧の傾きは何故できるか考えてみましょう。
初めに、空気が水平方向に至るところ一様な性質を持って静かに存在する(といっても空気分子は
"その場所"で、活発に飛び交っていますが)状態を考えましょう。このような気圧配置では、風は
吹きません。気圧は、"その上に乗っている空気の重さ"ですから、このような状態では、地上気圧
は何処も同じ値1013hPaです。1013枚のhPa等圧面が水平に平らに広がっているのを
想像してください。そのうちの上から1003枚目から1013枚目(地面すれすれ)までを図8
.2に示しています。

このような状態では、水平方向には気圧傾度がなく、空気は動かず、従って風は全く吹きません。
(垂直には、圧力勾配がありますが、重力と釣り合っています。)
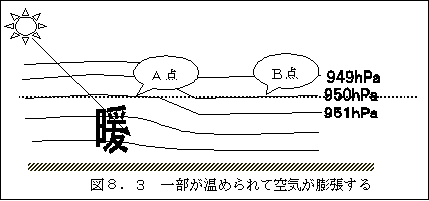
図8.2の左半分に太陽光線が当たったとします。太陽光線は、殆ど空気を素通りしますが、地面 を暖めます。そして暖められた地面が接している空気を暖めます。
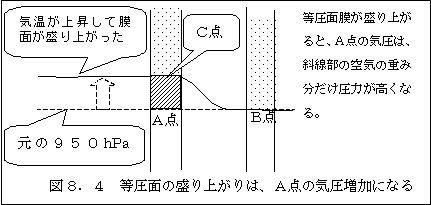
空気は、暖められて膨張し、地面に近い層は、少し厚みを増して、図8.3に示すように、水平に 広がっていた膜の一部が上に膨らみます。 図8.4は地上に比較的近い950hPa面の変化の様子を示しています。気温が水平方向に均一 であった場合には、950hPaの等圧面は水平に横たわって居ましたが、地面付近から熱が伝わ り温度が高くなったために、空気の分子運動が盛んになり、周囲に押し返す圧力が高まって、厚さ が膨らみ、等圧面の上に空気を乗せたまま上に膨らみます。その結果図の斜線を引いた部分の空気 の重さだけB点より気圧が上がります。
風は水平方向の気圧の傾きにより起こりますが、この様に気温分布が気圧分布を引き起こし、風の
原因になります。
<高層天気図は等圧面天気図>
地上天気図とは、海抜0mにおける気圧分布図と言うことが出来ます。同じように高層天気図とし て海抜3000mにおける気圧分布を描いて「3000m高度天気図」等が考えられます。300 0m高度において水平方向に気圧の傾きが無ければ、言い換えると水平方向の気圧差が無ければ風 は吹かないし、気圧の傾きがあれば、地衡風の式に当てはめて風の計算が出来ます。このように一 定高度の気圧分布を考える事は、地上気圧分布を考えることと殆ど同じように考えることが出来ます。 また3000m高度という上空にある平面のイメージもよく理解できます。
しかし、通常は高層の天気図として、一定高度の天気図でなく等圧面天気図が使用されています。 等圧面天気図と言われても慣れていない人には理解できにくいと思いますので、具体的に例を上げ て見ていきましょう。
例えば、3000m高度付近の気圧は約700hPaになっています。上から700枚目のhPa
等圧面が3000m付近を波打って広がっていると考えてください。その面から上には、何処も同
じ700hPa分の空気が乗っています。
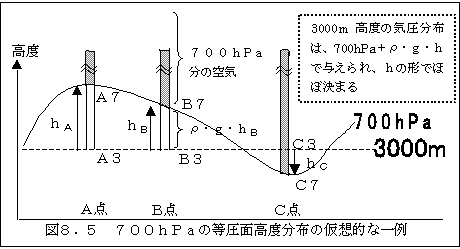
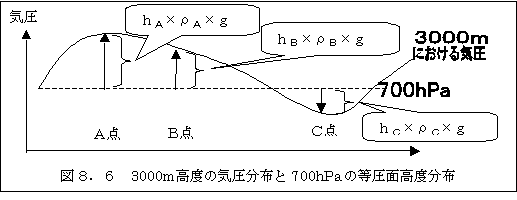
図8.5は、3000m高度(破線)と、その高度付近に広がっている700hPaの等圧面(実 線)の仮想的な一例を横から見たものです。
図8.5で、A点、B点、C点は観測地点3カ所です。それぞれの観測地点の上空3000m高度 上にそれぞれ、A3,B3、C3を、また、それぞれの上空の700hPaの高度にA7,B7、 C7と名前を付けましょう。A7,B7、C7の気圧は当然、総て700hPaの気圧になってい ます。
A3,B3、C3の気圧を計算してみましょう。
まず、A3の気圧は700hPaとA7~A3の単位面積の気柱の重さを足した値になります。
A7~A3の気柱の高さをhAとすると、気柱の体積は1(m2)×hA(m)ですから、密度を
ρA(Kg/m3)としますと、A7~A3の気圧差は、
hA×ρA×g
となります。ここで、gは重力の加速度9.8(m/s2)です。
従って、A3の気圧は700hPa+hA×ρA×gとなります。
同様に考えてB3の気圧は、700hPa+hB×ρB×gとなります。
C3の気圧は、C7がC3よりも低くなっています。C7の気圧は、700hPaよりもhC×ρ C×gだけ低く、700-hC×ρC×gとなります。
A点、B点、C点の3地点の気圧が分かりましたので、縦軸に気圧を取って気圧分布
を描きましょう。ρA、ρB、ρCをほぼ同じとすると、3地点の基準気圧700hPaとの差の
気圧分布はhA、hB、-hCに比例しており、図8.5で示された等圧面高度の分布とほぼ同じ
形が示されることになります。
具体的な例を見て内容がほぼ分かった所で、一般的なまとめを致しますと、「等圧面の高度分布か らその基準高度を引いた分布は、その基準高度における気圧分布にほぼ相似な分布が得られる」と 言えるでしょう。このために、上空の気圧分布の代わりに、その高度付近の等圧面高度分布を用い ることが可能になります。
さて、もう少し、3000m高度付近の天気図にこだわって、この高度の1hPa毎の等圧面の厚
さはどれくらいか計算してみましょう。1hPaの厚さをh(m)とすると、この間にある空気の
重さによって1hPaの圧力差が生じているのですから
1(hPa)=h(m)×ρ(Kg・m―3)×9.8(m・s―2)
の関係式が得られます。1(hPa)=100(Pa)=100(N・m―2)です。
従って1hPaの厚さh=100/ρ/9.8となります。すなわち、1hPaの厚さは、密度に 逆比例しています。空気の薄くなる上空では、次第に1hPaの厚さは大きくなって行くことが分 かります。
理科年表に載っている標準大気では、3000m高度の気温は、-4.5℃、気圧は、701.1 hPaとなっています。空気に対する状態方程式と言うのがあって、気温と気圧が分かればその空 気の密度が計算できます。状態方程式は、気圧をP、気温(絶対温度K=273.2+摂氏)をT、 密度をρとすると、P=ρ×R×Tと現されます。
Rは乾燥空気に対していつも決まった値で、気体常数と言います。その値は287(m2・s―2
・K―1)です。この式に3000m付近の標準大気の値を入れてみましょう。
ρ=P/(R・T)=70110/287/(273.2―4.5) =0.909(Kg/m3)
従って、3000m高度付近の1hPaの厚さhは、h=100/0.909/9.8≒10.3 mとなります。3000m高度付近に限れば、密度の変化はそれほど大きくないと考えられ、この 1hPaが約10mに相当することを考えると、700hPa天気図における高度差10mにつき 1hPaの気圧差と考える事ができます。
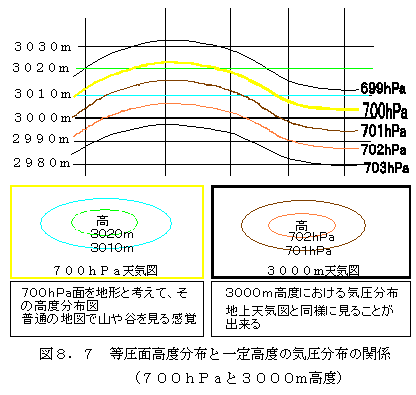
これらの特性を考慮して、3000m高度付近の1hPa毎の等圧面を仮想して描いてみると図8
.7の様に描くことができます。等圧面の高度が、その高度付近の一定高度における気圧分布と同
じような形を示すことを確認してください。
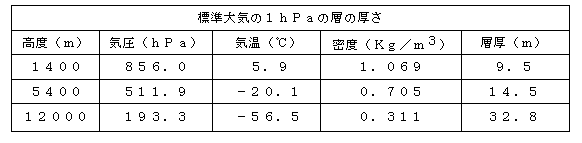
また、標準大気1hPaの層の厚さは、下の表の様になりますので、高層天気図で示される高度差
を水平方向の気圧差に換算すると、概略的には
850hPa(対流圏下層)天気図では、高度差10mが約1hPa、
500hPa(対流圏中層)天気図では、高度差15mが約1hPa、
200hPa(対流圏上層)天気図では、高度差30mが約1hPa
に相当すると見ることができます。
<等圧面高度と地衡風>
一定高度における気圧の傾きによって得られる地衡風は、既に見てきましたように水平面の中で 気圧が最も傾いている方向に距離をn、気圧をP、空気密度をρ、コリオリのパラメーターをf とすると地衡風vは、
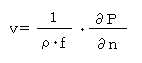
で与えられます。
しかし、現実には、高層の天気図は等圧面高度分布を通常用いていることが分かりましたので、
等圧面天気図の高度の傾きから地衡風を求める必要があります。
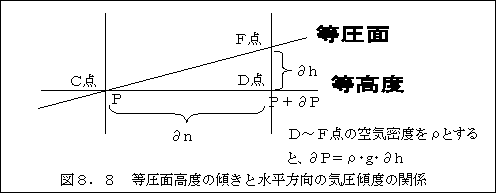
図8.8において気圧がPの等圧面がC点とF点を通っています。F点はC点から見て上ってい ます。C点とF点の水平距離は、∂nで与えられ、F点の真下でC点と同じ高度の点をD点とし ます。
F点及びC点は同じ気圧面が走っていますから、D点と、F点及びC点との気圧差は共に同じで、 ∂Pで与えられます。D点の気圧がF点より大きいのは、F点とD点との間にある空気の重さに よって与えられています。単位面積の気柱∂hの体積は、1・∂hで、密度がρですから、F点 とD点との間にある空気の重さはρ・g・∂hで与えられます。gは重力の加速度です。
先に「地衡風」の項で得ていた「気圧分布から地衡風を求める式」にこれらを当てはめ、「等圧
面の高度分布から地衡風を求める式」を作ってみましょう。
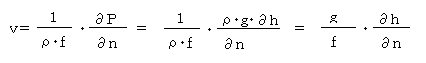
となりますから、
等圧面の高度分布から地衡風を求める式として
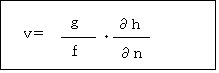
が得られます。ただし、ここでgは重力の加速度、fはコリオリのパラメーターで緯度によって値は決まります。hは等圧面高度、nは等圧面内の平面距離ですので、dh/dnは等圧面天気図の高度分布から読みとることが出来ます。
また、地衡風の特徴を以下のように纏めることが出来ます。

<等圧面天気図を用いる理由>
「等圧面の高度分布から地衡風を求める式」を見ていただいて分かりますように、等圧面の高度 によって地衡風を求めると、密度の項が無くなりました。密度は上空に上がると小さくなって変 化しますが、地衡風の式から密度の項が消えています。
コリオリパラメーターfは緯度だけによって決まり、重力の加速度gは、気象で扱う程度の高さ であれば、殆ど変化しないと言えます。したがって、等圧面天気図によって、高度分布を扱うと、 どの高度の(気圧の)天気図でも水平方向の高度の傾きで、地衡風の見積もりができます。
60mの高度差がある場合は、850hPa天気図でも、700hPa天気図でも、200hP a天気図でも、全て同じ地衡風になっています。かなり大ざっぱに言いますと、500h Pa天気図に見られる等高線の間隔は850hPa天気図に見られる等高線の半分くらいの間隔 になっていますが、これは、500hPaの風が850hPaの風の倍近い風速になっている事 を示しています。これが等圧面天気図を利用する理由の一つとなります。
等圧面天気図を利用する他の理由は、実際高度よりも気圧の方が気象学的には、大気全体の相対 的な高さを把握するのに便利であるからです。例えば、500hPaと言えば、地上気圧の約半 分ですので、大気全体の約半分が存在する高さと考えることができます。
そのほか、高さの座標を実際高度でなく気圧で示すと、観測値がそのまま、直ぐに用いられると 言う点です。高層観測は気球を飛ばして観測しますが、気球の実際高度は計算しなければ出ませ ん。それに対して気圧は気圧計で測りながら上昇していますので、今の高度は何hPaか直ぐに分 かります。
↑ 目次へ |