Flatterland - like flatland, only more so -	Cat: SCI Pub: 2001 #1519b
	Ian Steward	15816u/18116r

Title	Flatterland	フラッターランド
Index	From Flatland to Flatterland: The third dimension: Victoria's diary: The visitation: A hundred and one dimensions: One and a quarter dimensions: The topoglogist's tea-party: Along the looking-glass: Grape theory: What is a geometry?: Platterland: Cat country: The pardox twins: The domain of the Hawk King: Down the wormhole: What shape is the universe?: No-branes and P-branes: Flatterland: The tenth dimension:	序文: 三次元世界: ビクトリアの日記: 訪問は: 101次元: 1.5次元: トポロジストの茶会: 鏡に沿って: 葡萄理論: 幾何学とは何か: 扁平な国: 猫の国: パラドックスの双子: ホーキングの領域: ワームホールを通って: 宇宙はどんな形をしているか: NOブレインとPブレイン フラッターランド: 10次元の世界:
Tag
Why?	This book start: "A bee in the bonnet: An idea that buzzes around for years until one day it suddenly crystallizeds..."

Original resume	Japanese resume
>Top 0. From Flatland to Flatterland: In 1884, Edwin Abbott Abbott wrote a classic of scientific popularization 'Flatland'. The rather narrow Victorian attitude of A. Square are shattered by rumors of the Third Dimension, confirmed by a visitor (The Sphere) from that extra-dimensional realm. He had a second purpose; to satirize the rigid social structure of Victorian England, with its hierarchies of status and privilege. He made the females of Flatland mere one-dimensional lines, inferior to isosceles triangles, and vastly inferior to the circular Priesthood. Abbott was a social reformer who believed in equal educational opportunity for all social classes and genders. The fourth Dimension was hot intellectual property in Abbott's day. There is ample scope to play Abbott's game again in a new context.	0. フラットランドからフラッターランドへ: E. A. Abbpttの名作フラットランド (1884) の続編
>Top 1. The third dimension: Vikki happened to find her grand-grand father's handwritten script; 'Flatland' He, Albert, did die in prison. He claimed he had visited the Land of 3D himself, with the Sphere as his guide, a 100 years ago.	1. 三次元: 祖父Albertが行った三次元国 孫娘Vikkiは更なる冒険へ
>Top 2. Victoria's diary: But her father, Grosvenor, had burned Albert's book - What about freedom of speech?. Fortunately, Dad doesn't know how to work her computer. I didn't promise with Dad not to read it later. By now Victoria could pretty much recite Flatland by heart. She had also learned to mistrust it, having notices some absurdities.	2. ビクトリアの日記:
>Top 3. The visitation: The Mathiverse transcends Time and Space ... it transcends Intelligence and Extelligence. He said himself to be a Space Hopper; saying he can hop spaces. A space was an entire world! More than that, it was an entire self-contained universe. One-and-a-quater dimensions, would you believe? Infinite dimensions. Bent space and rippled space and space that blows itself up .... Space that's just disembodied dots. They all live inside some kind of Grand Unified Metaspace (GUM) known as the Mathiverse. He will bring a Virtual Unreality Engine (VUE) tomorrow night. Mathiverse transcends Time and Space... it transcends intelligence and extelligence... it transcends thought; it transcends transcendence itself. Mathiverse contain all vectors, matrices, permutations, combination, bijections, semigroups, transformations, relations, functions, functors, funtionals, algebraic group schemes, supermanifords, K-theries, M-theories, M-sets, power sets, subsets, supersets, and plain, ordinary, common-or-garden sets. Planiturthian universe: The fundamental unit of the Planiturthian universe is the philosophone, a unit of logic so tiny that only a philosopher could hope to split it. Planiturthian beauticians would like to think that the Planiturthian universe is built from beauty; for whatever attributes the Mathiverse might have, beauty is paramount among them. Clockwork Universe of Isaacnewton; Absolute and Uniform Space. But Planiturthians have now decided that they don't actually live in Spaceland at all. They live, perhaps, in Curvyspace. Or it is a Waveworlds? Or are they gambolling in the Quantum Fields. Why snowflakes had sixfold symmetry. He traced it to a packing problem. if ice was mde of tiny spheres and if those spheres packed together as closely as possible, the the crystal lattice of ice would have a hexagonal structure. atoms pack together in whatever arrangement makes their energy lowest, and basically that means close-packing.	3. 訪問者: マセバース：時間も空間も超越し、知能・外部知能・思考も超越し、超越も超越する。 VUE：全ての別得、行列、順列、組合せ、双射、準群、変換、関数、汎関数、超多様体、K理論、M理論、M集合、冪集合、部分集合、超集合、....を含む。   Planiturthian
>Top 4. A hundred and one dimensions: 4D expression: Additional slanting line; Chalk - Cheese line, or replace Chalk with Past and Cheese with Future. Your present work is wafer-thin!. Existence of a Fourth Dimension, merely appearing from thin air within a locked room, growing from a point to a small sphere to a larger sphere, and then shrinking back to nothingness. Multidimensional: It's all to do with variables - quantities that can change. Dimension is a geometric way of referring to a variable. Time is a nonspatial variable, so it provides a fourth dimension, but the same goes for temperature, wind-speed, or the number of termites in Tangentia. A point in n-D space ought to correspond to a list of n coordinates. So n-dimmenional space itself can be thought of as the set of all such list. The set of all points that lie at a fixed distance from a chosen point is known as an (n-1) dimensional hypersphere. Land of Dotcom; error check of coding theory: If you coded every message by replacing every 0 by 00 and every 1 by 11. Then a message such as 110100 would code as 111100110000. If this ire received as 111000110000, with an error in the second pair of digits. Single error correspond to moves along an edge of the n-cube; double errors correspond to moves along two successive edges, and so on. How many single-digit changes it takes to convert one into the other. In fact, it's just the distance between them measured along the shortest path formed by edges of the hypercube. Each edge has length 1 unit, so in the Hamming metric the opposite corners of a square are 2 units apart, not √2 units apart. Using color Color is a pretty arbitrary way to represent something like blue-red axis; Color Machine instead of Time Machine. Planiturthian multiverse: Physical reality has many interpretations, and the one presented to us by our sense organs need not be the only possibility. Our universes could be just one of a infinite variety of universes that might have happened instead, so that we occupy just a wafer thin slice of a vast multiverse.	4. 101次元: In a telect coding, numbering was used 11, 22, 33 instead of simple 1, 2, 3.   'Simplex method'
>Top 5. One and a quarter dimensions: Fractal Forest: There are crinkles on the crinkles, and crinkles on the crinkles .... In the fractal Forest, geometry goes on for ever and dimensions come in fractional amounts. The edge of this snowflake, for instance, has approximately 1.26186 dimensions. It's not exactly one and a quarter. In order to double the size of a shape, the number of copies you need is 2 raised to the power of the dimension; square needs 2^2=4, and cube needs 2^3=8 what power of 3 makes 4?; 3^1=3, and 3^2=9 x= log4/log3 = 1.261859507 crinkliness measure the fractal dimension. Sierpinski gasket is made from three copies, each half the size; log3/log2=1.5850 Sierpinski carpet is made from 8 copies, each 1/3 the size; log8/log3= 1.8928 Menger sponge is made from 20 copies each 1/3 the size, so its dimension is log20/log3=2.7268. Quadratic City: Pick a taxi, located at A+Bi, and the color the intersection of A avenue and B street white if taxi A+Bi eventually escapes, but black if it doesn't. Grand Central Station itself is 0+0i. Suppose to a taxi 2+3i to 2 avenue and 3 street, and I want to go back to Grand Central Station. What do I do? The City authority allowed that a taxi could make a square trip; if you were on X+Yi, then squaring takes you to (X^2 - Y^2) avenue and 2XY street. But the number should be within 2 km of Grand Central Station; like a tax -0.1+1i. whether a general point gets colored black or white is algorithmically undecidable; which means that no computer program can be guaranteed to give an answer. Fractal dimension 2: the boundary is curve; same fractal dimension as a solid disc, or a square. This is as big as you can get for a curve in the plane. Something which seems very complicated may in fact arise from simple rules. So the trick is to understand the rules, not the complicated behavior that follows from the rules. We have to be sensitive to new kinds of pattern,, such as fractals; which can lead us to new types of rule. Vikki felt like that; "There's a lot going on? Somewhere to take my mind off home."	5. 1と1/4次元 フラクタルの森 フラクタル次元         二次元複素数の町
>Top 6. The topologist's tea party: Topologica; the rubbeer-sheet continent, which can bend, stretch, compress, distort and deform, but not tear or break. douhnut with two holes and tea pot: a tea pot has a hole for putting the tea into the pot; but that hole onle goes in. It doen't cou out again. But a hole that goes in and doew come out again is called a tunnel (a spout). a tube is just a long, thin hole; the Rubger-sheet Continent, long and thin have no significance. A hole is a hole, whatever its size or shape. a twisted cow; two different sides are actually just different parts of the same side. an edge can separte one side of a flat surface from the other, the Moobius has edges, too. A Klein bottle; basically, it's a tube that bends round and joins up to itself. But as sit bends round it kind of passes trhough itself and truns inside-dout, so the surface all joins up. Kummer's surface (studiy by Kummer in 1864); Kummersche Flache; are a family of quartic surfaces given by the algebraic equation. Typical defining equation; x^4+y^4+z^4 - (y^2*z^2+z^2*x^2+x^2*y^2)-(x^2+y^2+z^2)+1=0	6. トポロジストの茶会:
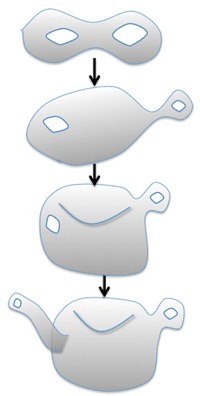
>Top 7. Along the looking-glass: Infinityville ∞: Infinity plus one equals infinity, and infinity minus one equals infinity; which is why parallel lions meet there. I know you're a line, so that ought to make no difference, but you have a sense of left and right, and that has changed. Your left shoe has changed into a right shoe, and you right foot has changed into a left foot. It is as though you have passed through a mirror, but there isn't a mirror. The Projective Plain is one-sided surface. We're not standing on the surface; we are in the surface like drawings inscribed upon it. And the geometry of the Projective Plain means that when you slide an object along a lion until it gets back to where it started from, it returns as its own mirror image.	7. 鏡に沿って: 射影幾何学 鏡面体
>Top 8. Grape theory: Abstract properties: Seven points are to be arranged in lines. Each line contains exactly three different points. The following conditions must hold: Any two lines have exactly one point in common. Any two points lie in exactly one common line. Logically, it makes no difference what names we call them. As the great Planiturthian mathematician Davidhilbert aide, the logical structure of geometry should make equal sese if the words point, line and plane are replaced by beer mug, chair, and table. Names don't matter. Four points forming a square; straight lines should be in such a geometry. They're the sides of the square and its diagonals. Finally, we add a line at infinity. The top and bottom of the square are 'parallel' in the sense that they don't meet. So we add to each a point at infinity. Similarly for the left and right sides. The diagonals form a third pair of parallel lines. The diagonals of a square don't meet on the grid. In this version of the Euclidean plane, only the four corners of the square exist. The diagonals don't meet at a corner, so the center of the square doesn't count. Since they don't meet on the grid, I consider them to be parallel.	8. ブドウ理論: 有限射影幾何学 Line at infinity:
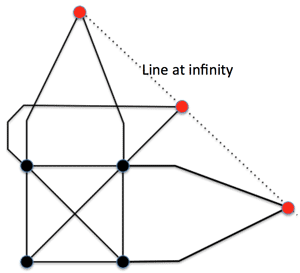
>Top 9. What is a geometry? What you've been looking at are rigid motions in the plane. Translations, rotations, reflections. Those transformations characterize the geometry of Flatland: The only meaningful geometric properties of Flatland are the ones that are unchanged after a rigid motion. Invariant. Properties like length, area, angle, and so on. Whereas in topology, the range of allowable transformations is far greater. Length, area, or angle are not topological invariants. They can all be changed by continuous transformations. They can change in projective geometry, tool - but in projective geometry the permitted transformations are projections, so straight lines stay straight. 'Straightness' is invariant in projective geometry. But it's not invariant in topology, because there you can take a straight line and bend it. Symmetries: a symmetry is a transformation that leaves an object looking exactly the same as it was before the transformation was performed. Every Square in the Euclidean Plane has eight rigid-motion symmetries. rotate through one right angle. rotate through two right angles. rotate through three right angles. rotate through four right angles; identity transformation. (trivial) The only thing that matters when describing a mathematical transformation is where everything ends up, relative to where it started from. The route it takes on the way is ignored. Group property: any two symmetry transformations carried out in succession lead to a symmetry operation. How many reflectional symmetries? - Four. Rotate the square, or reflect it about the diagonal through your chosen corner. That makes eight ways to reposition it. For the same reason, every Pentagon has ten, every Hexagon twelve - the number of symmetries of a regular polygon is twice the number of its sides. A genuine Circle ha infinitely many symmetries. A poor Equilateral Triangle has only six symmetries - three rotations, three reflections. An Isosceles Triangle has only two; the identity and a refection. An irregular Triangle has only the identity symmetry. A Line as Flatland women has two symmetries; the identity and rotation through 180º. In fact there are four rigid motions; the third is to reflect the Plane in a mirror that runs along the line. And the fourth? Reflect in that mirror and rotate it by 180º.	9. 幾何学とは何か: Invariant 不変の
>Top 10. Platterland: Platterland seems to shrink as it approaches the rim of the disc. Suppose there is some kind of 'temperature' effect; the rim is very cold indeed, and the center is warmer; The length of the strides shrinks very rapidly as the big strider nears the rim. he is infinitely far away; it own inhabitants perceive it as being of infinite extent. Euclidthegreed axioms: Any two points may e joined by a unique straight line. Any to lines are either parallel or meet at a unique point A right angles are equal. Given any line, and any point not on that line, there is a unique line through that point that is parallel to the given line, cusing photon decay.	10. 扁平な国: 周辺に行くほど空間が縮むような国。端まで行くのに無限の時間がかかる
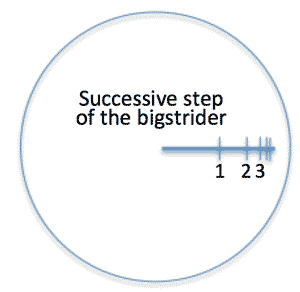
>Top 11. Cat country: It it (until replaced by something else) the space in which all Plantiturthians live - the space from which the are built. Rhinoscleromata killed his cat and kept it alive, all at the same time. In this country, everything looks growing; it's not. the visitors are shrinking. a pebble kept changing is surprising ways; sometimes rugged, rippled, smooth, hairy, as if forests were growing on it. Atoms aren't exactly particles, and they're not exactly indivisible. Electron; sometimes behaving line a wave, sometimes behaving like a particle. You can call them 'weevils' if it makes you feel happier. (quantum wave functions) Uncertainty Principle, discovered by Werner he is en berg; if you try to measure the position of a particle, then you disturb its quantum wave function; weird Physicists have an astonishing habit of choosing really bad names Relativity theory, but lights peed is absolute. quarks; the proton is two up quarks plus one down quark; the neutron is tow down quarks plus one up quark. The omega-minus particle is three strange quarks. There are six flavors of quark; up, down, top, bottom, strange, and charm. How do Planiturthians experience the Mathiverse, then? Instead of a VUE, they use an IMAGER. Imagination, Mathematics, Analogy, Generalization, Extrapolation and Recursion; 2D, 3D, 4D, ... nD, ∞D. They extrapolate concepts from their 3D experiences, so planes extrapolate to hyper planes, spheres to n-spheres. Finally, they recursively go back to the imagination state and start all over again; to the far more sophisticated and intricate geometry of the quantum universe.	11. ネコの国: 量子論 シュレレジンジャーのネコの話：その生死が確率的であること
>Top 12. The paradox twins: Paradox twins: the speed of light being the same however fast you're moving, but lengths contracting and time expanding - that's true, but only if y9ur speed i uniform. if you accelerate, it all gets more complicated. Acceleration is not a relative quantity in Albereinstein's theory. Even the speed of light ceases to be constant for an acceleration observer. And the source of asymmetry between the twins is that Twindledumber went off in a spaceship, and he accelerated quite fast to get up to lightspeed, and then he accelerate again when rounding the star, and finally he decelerated to avoid smashing into his brother at lightspeed when he arrived home again. Whereas Twindledumb stayed in an inertial frame - no acceleration. So it's not symmetric, and that's why Twindledumb has aged forty years while Twindledumber has aged only two days.	12. パラドックスの双子: 特殊相対性理論 双子の兄は準高速で飛び出し、弟が地球で待っていた場合、運動中の兄の時間がゆっくり進むので、兄の帰還後、兄弟に年齢差が生じるパラドックス
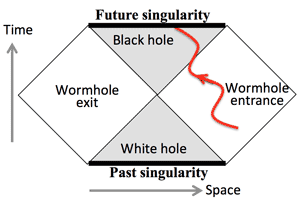
>Top 13. The domain of the Hawk King: Schwarzchild radius: In 1915 Karlschwarzschild solved the Einstein equations for the gravitational field around a heavy sphere in a vacuum. His solution behaved very strangely at a critical distance from the center of the sphere. In 1967 Johnarchibaldwheeler called such a region a black hole. First the star shrinks symmetrically until it hits the Schwarzschild radius; all the mass has collapsed to a singular point (singularity). From outside, all you can detect is the event horizon at the Schwarzschild radius, which separated the region from which light can escape from the region that's forever unobservable from outside. Once inside a black hole, the roles of space and time are reversed. Just as time inexorably increases in the outside world, so space inexorably decreases inside a black hole. Now, the spacetime topology of a black hole is asymptotically flat - its 'mouth' opens out and becomes flat at large distance. The technology of 3001 will be able to build black holes. The time-reversal of a black hole is a white hole; no particle can fall, but from which particles may from time to time be emitted as the sudden explosion of a star's worth of matter, coming from a time-reversed event horizon. Light cone: any event in space-time has associated with it a light cone, formed by two 45 degree diagonal lines that pass through it.; corresponding surface really is a double cone. The forward region contain the future of the event. The backward region is its past. All the events that could possibly have influenced it. Everything else is forbidden territory; have no possible causal connections with the chosen event. Geodesics: Alberteinstein wasn't keen on forces. He preferred o think geometrically. The paths that particles follow, in the absence of forces such as gravity, are called geodesics. Alberteinstein incorporated gravity not as an extra force, but as a distortion of the structure of spacetime. A time machine: lets a particle or object return to its own past, so its world-line, a timelike curve, must close into a loop. So instead of asking, 'Is time travel possible?', 'Can closed timelike curves exist?' Use of the Paradox Twins; they experienced a time discrepancy; in conjunction with a worm hole, that time discrepancy can be turned into a closed timelike curve. World-lines: At first, those lines have a lope of less than 45º, so they're not timelike, and it's impossible for material particles to travel along them. But as the black end of the wormhole zigzags back and forth, at some moment that line achieves a 45º slope. And once this 'time barrier' is crossed, you can travel from the white end of the wormhole to the black one through normal space - following a timelike curve. And once you've arrived there, you can return through the wormhole, again along a timelike curve; effectively travelling instantly from the black end to the white end. And now you're in the same place as your starting point, but in the past!	13. ホーキングの領域: 一般相対性理論           ブラックホールの時空トポロジー 光円錐 測地線 タイムマシン           ワームホール
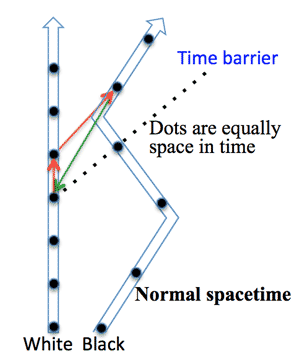
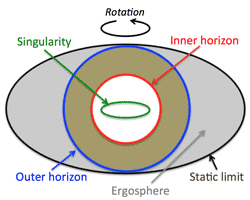
>Top 14. Down the wormhole: Kerr Black Hole: Kerrnewman's black hole; which rotates and has electric charge. It is almost a miracle that an explicit formula for the solution exists; There is no longer a point singularity inside the black hole. Instead, there is a circular ring singularity, in the plane of rotation. Penrose map shows that any matter entering a static black hole has to fall into the singularity - but in a rotating one, it need not. It can either travel above the equatorial plane, or pass through the ring. Signals or matter that penetrate the outer horizon can't get back out again; signals or matter emitted by the singularity itself can't travel past the inner horizon. Further out still, but tangent to the outer horizon at the poles, is the static limit., they have to rotate in the same direction as the black hole, although they can still escape by moving radically. Between the static limit and the outer horizon is the ergosphere. If you fire a projectile into the ergosphere, and split it into two pieces, one being captured by the black hole and one escaping, then you can extract some of the black hole's rotational energy.	14. ワームホールへ向かって: タイムトラベル 回転ブラックホール Penrose Map: Wormhole Entrance - Exit
>Top 15. What shape is the universe? It often helps to take a step back and see the whole more clearly, as well as to take a really close-up look at all the nuts and bolts. In Virtual Unreality; Vikki imagined she could fee the universe shrinking. a lot of vacuum will pull apart into electrons and antielectrons. A billion times as many as there were just now. In backward time, they're unannihilating each other. And that means we have only thirteen seconds left; until the end of the universe! It's all gone sort of ... transparent. That's the neutrinos decoupling from the rest of matter. The temperature must be up to about ten billion degrees now. The temperature's up to thirty billion degrees, that's all - too hot for any atomic nuclei to stay together. It's just independent particles now. That's why we can't see much going on any more. Ah. The unannihilation of the hadrons; the heavy particles, like protons, antiprotons, neutrons, antineutrons, have multiplied a billionfold. More vacuum converted into particles and antiparticles. It'll soon run out altogether; the supply of vacuum. Vacuum is empty space, and the space is running out. Anyway, a quantum vacuum isn't really empty; it's a seething torrent of particle and antiparticles winking into existence and back out again. The time-wisps are shrinking - time is literally running out, there's only a hundredth of a second left. And we're up to a hundred billion degrees. Three hundred billion degrees and in a thousandth of a second ... see how tiny the time-wisps have become .... it will disappear. They stared at empty metaspace. No particles, no vacuum, no temperature ... and no time-wisps.; which is known as the Big Bang! What an anticlimax! But in forward time, it's like a sudden humongous explosion! Space, time, and matter all coming into being from absolutely nothing.	15. 宇宙はどんな形をしているか: 宇宙の形   仮装非現実 時間を反転してブラックホールに迫る   真空のエネルギー
>Top 16. NO-branes and P-branes: Four forces: Gravity: very weak force; a long-range force; it's what holds the universe together. Elecgtromagnetism: both magnetism and electricity have fields associated with them. two different aspects of the same thing; Electromagnets can turn electricity into magnetism, and dynamos can turn magnetism into electricity. intrinsically stronger than gravity, but it comes in two kinds - positive and negative. those tend to cancel out, the dominant large-scale force is gravity. photon carries electromagnetic interaction. Strong nuclear force (Strong interaction): stronger than 100 time of electromagnetism. it acts only a short range - about a quadrillionth (10^-15) of meter; it's what keeps protons and neutrons together in the atomic nucleus. no strong nuclear force, no nuclei, no atoms, no molecules. Gluon carries strong nuclear force; acts between quarks. Weak nuclear force (Weak interaction): W-boson and Z-boson carry weak nuclear interaction; leptons don't feel the strong nuclear force, but they feel weak nuclear force. weak nuclear force is a lot weaker than the strong nuclear force and has about a hundredth of its range.　(10^-18 m) Grand unification theories (GUT): predicts additional gauge bosons (X-boson and Y-boson), which are supposed to interact between quarks and leptons. Fourth fundamental interaction, gravity, may also be carried by a boson named graviton: A new particle has to be introduced with care; otherwise all it will do is disrupt the logical harmony of the Standard Model, with disastrous consequences. One of the main features of the Standard Model; as a symmetrical geometry. Time-reversal: if the universe run backwards in time, it obeys the same laws that it did forward time. but charge-reflection symmetry is broken at the time of the Big Bang. all four forces of nature were unified into a single force; the differences we now see arouse hen the original symmetry broke. String theory: String theory seemed to be telling physicists that if they wanted an effective theory of quantum particles, then gravity would be a necessary consequence. All consistent string theories include gravitons. all five superstring theories fit into a bigger 11D picture known as M-theory. there are five different ways to shrink away one of the 11D of M-theory, and they lead to those five 10D superstring theories. So all five competing theories are actually part of the same Big Picture. But there's no experimental evidence.	16. : NOブレインとPブレイン: 大統一理論 (GUT, Great Unification Theory) 素粒子 Standard Model: Quarks Gauge bosons up (u) charm (c) top (t) gluon (g) ch ⅔ sp ½ ⅔ ½ ⅔ ½ ch 0; ma 0 1 down (d) strange (s) bottom (b) photon (γ) ch -⅓ sp ½ -⅓ ½ -⅓ ½ ch 0; ma 0 1 Leptons   electron (e) muon　 (μ) tau (τ) Z boson (Z) ch -1 sp ½ -1 ½ -1 ½ 0 1 electron neutrino (νe) muon neutrino (νμ) tau neutrino (ντ) W boson (W) ch 0 sp ½ 0 ½ 0 ½ ±1 1     graviton boson? (G) Higgs boson (H)     ch 0; ma 0 sp 2 ch 0 sp 0
>Top 17. Flatterland: Victoria Line was going home; it would be wonderful to return to Flatland and discover it has hidden dimensions that on one had ever suspected. The shadow world and the ordinary world of Flatland meet along lines - not jut one line, but all lines. A ghostly image appeared in front of her VUE-enhanced senses. It was - an octagon. Mother is pentagon. And you are much high in the social hierarchy. -er indicate the comparative; X-er is like X, only more so. Like Flatland, only more so. The more-so is what the Space Hopper called the Shadow World. FLATTERLAND, the heading said. Then, Supersymmetric Sister! The shadow world of gender equality awaits. Superiority, eve. If you want to raise your station in Life, click here and be empowered. Click. .... Ad a new universe opened.	17. フラッターランド:
>Top 18. The Tenth Dimension: Seen from a 10D supermanifold, it was astrange world, with the austere beauty of a payge from Einstein. A sprawling, humming world of 3D shapes tacked together along 1D time; People lived peoplish lives, ae peoplish food, drank peoplish drinks, made peoplish love, bore peoplish children, and died peoplishly in a 3+1D universe and never thought it the least bit curious. As long as nothing disturbed that perception, it was tue. But times and spaces were changing in Spacetimeland ...	18. 10次元の世界:

Comment

a

a