Original resume |
Japanese resume |
>Top 1. To Infinity and Beyond::
- The infinite is a concept so remarkable, so strange.
- Infinity makes space seem small.
- Infinity fascinates because it gives us the opportunity to think beyond our everyday concerns, beyond everything to something more - as a subject it is quit e literally mind-stretching. As soon as infinity enters the stage, it seems as if common sense leaves.
- Reluctant scientists have found themselves having to handle such concepts as particles travelling backwards in time, or being in two opposite states at the same time.
- Richard Feynman said, "It is my task to convince you not to turn away because you don't understand it. You see, my physics students don't understand it either. That is because I don't understand it. Nobody does."
- Infinity can be like a deer, spotted in the depths of a thick wood You will catch a glimpse of beauty that stops you in your tracks, but moments later you are not sure if you saw anything at all. Then, quite unexpectedly, the magnificent animal stalks out into full view for a few, fleeting seconds.
|
1. 無限とその先:
- 無限とは、画期的で奇妙な概念
- 無限は、空間を小さく見せる。
- 無限を考えることは日常を超越し、精神を拡張するテーマである。それは常識の通用しない世界。
- 科学者も素粒子が、時間を遡ったり、同時に反対の状態で存在することをしぶしぶ認めてきた。
- ファインマン曰く、"わからないから席を立とうとする人を引き留めるのが私の役目です。物理専攻の学生達も理解できていないのです。それは私も、そして誰でも理解できないことなのです。"
- 無限は森の奥深くいる鹿のようだ。山道に急にその美しい姿を現したと思った瞬間すぐいなくなる。そしてふいにその美しい姿の全貌を見せたかと思うと、次の瞬間すぐ消え去るのだ。
|
>Top
2. Counting on your Fingers:
- Counting a sequence of number, one after the other, is a practice that is ingrained in us from childhood. It is part of human nature to like order, to see patterns even where no patters exist.
- The Centaurus constellation; Alpha Centauri is the nearest to ours, a mere 4 light years distant; Beta Centauri (or Agena) lies 190 light years away. Our Sun is much closer to Alpha Centauri than Agena is.
- >Top The ellipsis (...) the end of the sequence; for mathematicians it means 'and so on without any end'.
- Zeno's paradox (5C BC):
Achilles is kind enough to give the tortoise an initial advantage. In a small time, Achilles has reached the point that the tortoise started from. By now, though, however slow the tortoise walks, it has moved on a little way. It still has a lead. In an even smaller amount of time, Achilles reaches the tortoise's new position - yet that extra time has give the tortoise the opportunity to move on. So the endless race carries on. Achilles eternally chasing the tortoise but never quite catching it.
- In early 1900s, Einstein imagined freezing a beam of light, not by taking a snapshot in time but by riding alongside it as the same speed. Now, the light was stopped. Einstein made the remarkable leap of thinking that light would always move at that one particular speed, however fast you moved towards it or alongside it. Fixing light to a single speed (300K km/s) changes the apparent nature of reality.
|
2. 指折り数えて:
- 数を連続して数えることは子供の時からの習慣。規則正しくは人間の本質で、パターンがなくてもパターンを見ることができる。
- ケンタルウスα星は、わずか4光年の最も近い恒星。ケンタルウスβ星は190光年離れている。α星と我々の太陽の方がずっと近い。
- 省略記号 (...)は連続の終わりを示す。数学者にとっては、それは"以下限りなく続く"を意味する。
- ゼノンのパラドックス(5C BC):
アキレスは亀のスタートの際のハンディキャップを与えた。わずかの時間で、アキレスはアキレスは亀のスタート地点に到達する。だが亀はどんなに遅くともその時間までにわずか先行している。アキレスはその場所にさらに短い時間で到達する。だがその間、亀の方も少し先に行っている。これを繰り返してもアキレスは永遠に亀に追いつけない。
- 1900年代始め:アインシュタインは光の速度を止めようと考えた。スナップショットを撮影するのではなく、光と併走することを考えた。そうすると光は止まって見えるはずだ。だが光はいつも一定の速度で進む。そのことが現実の見え方をすっかり変えることになった。
|
>Top 3. A Different Mathematics:
- The infinite series of switching on and off, the light bulb ends up in both states; 1, -1, 1, -1, 1, -1, ...
- Realists will point out that the bulb will have blown long before an infinite number of switchings is reached, s it will definitely be off.)
- Pythagoreans considered 'what is outside heaven' to be infinite, whereas Plato thought there was nothing outside the bounds of heaven and the infinite managed to fit within the universe.
- Aristotle: The infinite can't be a thing, any more than number or magnitude can be a thing. If a body can have this property - if there can be such a thing as an infinite body. This he counter by his definition of a body as something that is 'bounded by surface' as infinity cannot be completely bounded or it wouldn't be infinite.
- If there were no infinity, then time must have a beginning and and end, lines can't be indefinitely divided, numbers must stop.
- 'is' could mean either something that is actually in existence, or something that has the potential to exist.
- Whether infinity was real or unreal, comprehensible by the human or the divine, would occupy philosophers, but Aristotle's move of infinity into the virtual world of the potential made the mathematics work. Even so, this dismissal of the ultimate did not stop others from working with larger and larger numbers, as if they were trying to find a way of describing the infinite itself.
|
3. 風変わりな数学:
- 電気の点滅のような、1,-1の連続する数を考える。究極には1か-1か?
- 現実主義者は、無限に到達する以前に電気は切れてしまうので、offしかあり得ない?
- ピタゴラス派は、'宇宙の外'にあるものとした。プラトンは宇宙の外には何もなく、無限ですら宇宙の中にあるとした。
- アリストテレス:無限は、数や大きさであって、物ではない。無限という物ならばなんらかの属性を持ち、境界があるはず。無限にはそのような境界はない。
- もし無限が存在しなければ、時間にも始まりや終わりがある。直性は分割できず、数にも終わりがあることになる。
- 'is'という単語は何かが実在しているか、実在する可能性があることを意味する。
- 無限が現実か非現実か、人間にとって理解可能か神の領域かは、哲学者を悩ませてきた。だが、アリストテレスが、無限を可能性というバーチャルな世界に納めることで、数学は成立することになった。だが、究極的に排除しても、ますます大きな数を扱うことの終わりを意味しない。それは無限そのものの記述への道筋かのようである。
|
>Top 4. The Power of Number:
- a googol: one with a hundred zeros following.
- a googolplex is one with a googol noughts after it.
- Plato: could only conceive of an ultimate form what was finite.
- Aristotle; saw the practical need for infinity, but still felt the chaotic influence of apeiron (<Greek 'unlimited) was too strong and so came up with the concept of potential infinity - not a real thing.
- Plotinus, born in AD 204, made a specific one-to-one correspondence between God and the infinite.
- Pythagoreans had designated six as the number of the universe.
- With a myriad as the biggest named numbers, it was easy enough to describe a myriad of myriads: 100,000,000. Rather than give 100 million a specific name, he described all the numbers up to 100,000,000 as the numbers of the first order.
- A myriad of myriads then became the unit for a second order, so the biggest number in the second order was this unit of units: 100,000,00002. Thus, the next period began with this number and went up to 100,000,000 times bigger.
|
4. べき乗数:
- googol: 10の100乗, 10100
- googolplex: 10のグーゴル乗, 10googol
- プラトン: 究極数は有限と考えた。
- アリストテレス: 無限の可能性は考えた。但し現実の数でないとした。
- プロティノス (AD 204): 神と無限の間を1対1対応を行った。一者から流出した理性の働き (太陽の光)
- ピタゴラス派は、6を宇宙の数を見なしていた。
- 大きな数にミリアド(1万)という名称を与えると、ミリアドのミリアドは100,000,000 (1億)になる。これに個別の名を与えるのではなく、1億までのすべての数を第1階数と呼んだ。
- 1億は、第2階数となる。第2階層の最大数は、1億の2乗となる。このようにして、その上の階層は、この1億倍となる。
|
>Top 5. The Absolute:
- Jewish: 'cabbala', ten properties or components. God had delivered ten commandments to human creature with ten figures and ten toes.
- Greek were particularly fond of seven.
- Christian: in the book of Genesis creation took six days to complete.
- China: considers 8 is a lucky number.
|
5. 絶対数:
- ユダヤ教:'カバラ':10を神聖な数。十戒
- ギリシア:7を特別な数
- キリスト教:6を特別な数。天地を6日で創成した。
- Cf: 中国; 8を幸運数
|
>Top 6. Labelling the Infinite:
- Symbol of numbers:
arrived from India via Arabic world, and came to Western attention in 13C thanks to two books; the earlier book was written by Al-Khwarizmi (9C); assumed to give us mathematical term 'algorithm', meaning a series of rules for solving a mathematical problem.
- √2: now called irrational, because they can't be made out of a ratio of other numbers. There is no way to represent them as a fraction.
- by the middle ages, the existence of the irrational numbers was grudgingly recognized, even though they were still treated with deep suspicion.
- Michael Stifel (16C), German mathematician, who is best known for investing logarithms, who pointed out that irrational numbers were valuable because they could explain things that couldn't be managed with rational numbers alone. However, Stifel grumbles that irrationals are not true numbers but lie 'hidden in a kind of cloud of infinity'.
- π (< Greek periphereia): transcendental number, the name given to irrationals that can't be fitted to a suitable finite equation.
- Just as irrational does not suggest lacking rational thought, transcendental has nothing to do with the mystical associations the work has picked up in the last few years. I merely says the the number transcends - is outside of - calculation by equation.
- π26=1+12+14+18+116+... (L. Euler, 1735)
- π2=21×23×43×45×65×... (John Wallis)
- >Top ∞ denote Infinity: first appeared in the work of English mathematician John Wallis, 1655.
- This was not just the year of Newton, but also of Descartes, Fermat, Harlley, Pascal and Hooke. Wallis was born in 1616. Isaac Newton , born 26 years later. Both boys lost their fathers when they were young. Newton's was a farming family, putting pressure on him to stay away from academia, while Wallis's family encouraged the boy's education.
- Particular symbol ∞:
- from the old Roman sign for 1000 ⊂|⊃
- from a closed-up version of of the last letter of Greek omega (ω)
- infinity of a loop, or Möbius strip.
|
6. 無限に名称をつける:
- 数字のシンボル:
インド経由アラブ世界に伝わり、13Cに二つの本によって西欧に伝わった。その一つがアルフワリズミ (9C)の著書で、アルゴリズムの語源とされている数学者である
- √2:
今や無理数と呼ばれ、他の数の比で表せない数である。
- 中世には無理数の存在は、懐疑的にしぶしぶ知られていた。
- ドイツの数学者Michael Stifel (16C):対数の発見で有名。無理数の価値を評価。但し、無限の雲に隠れた存在とした。
- あああ
- π (ギリシャ語の円周):超越数。無理数であり、かつ有理係数の方程式からは導けない。 (代数的でない数、カントールによればほとんどの実数は超越数)
- π26=1+12+14+18+116+... (L. Euler, 1735)
- π2=21×23×43×45×65×... (John Wallis)
- 無限∞:
英国人数学者John Wallis, 1665が使用。
- この記号の語源は
- 古いローマ数字の千 ⊂|⊃
- ギリシャ文字最後の小文字 ω
- メルビスの輪
|
>Top 7. Peeking under the Carpet
- Carl
Friedrich Gauss (1977-1855):
- wrote, "The infinity is only a manner of speaking (façon de parler), in which one properly speaks of limits to which certain ratios can come as near as desired, while others are permitted to increase without bound."
- Galileo Galilei (1564-1642):
- You can work through each of the counting numbers and assign each its square. For example,
1→1, 2→4, 3→9, 4→16, 5→25, ...
- In that sequence, we missed out 2,3,5,6,7,8, and so on, from the squares. In the short list we looked at, there were 25 numbers, but only 5 squares.
- Carry on all the way to infinity. You must have a square corresponding to every single number. There are an infinite number of both roots and squares.
- The attributes, 'equal', 'greater' and 'less' are not applicable to infinite but on to finite quantities.
- There could be two different infinities, one clearly a subset of the other, that nonetheless are of the same size.
- This made it possible for Galileo's two concentric wheels to cover the same distance despite their differences in diameter.
|
7. カーペットの下から覗く:
- C. F. ガウス (1977-1855):
- 無限とは、話し方であって、ある比率が限りなく近づいたり、あるいは限りなく増加したりすることを言う。
- カリレオ・ガリレイ (1564-1642):
- 自然数の、その平方数を割り当てることができる。
1→1, 2→4, 3→9, 4→16, 5→25, ...
- その平方数には、2,3,5,6,7などが抜け落ちている。上の例では、25の数の内、5つだけが平方数である
- これを無限に繰り返す。その数にも対応する平方数がある。つまり根も平方数も無限にある。
- 等しい、大きい、小さいという属性は無限には当てはまらない。それは有限の場合の性質のある。
- 以上のように、2種類の無限があり、その一つは他の部分であるが、そのサイズは同じとなる。
- これはガリレオの2つの同軸の輪が半径が異なるにもかかわらず同じ距離を進むことを可能にしている。
|
>Top 8. The Indivisible Mystery:
- John Wallis:
- the inventor of the symbol ∞, who formalized the theory of indivisibles and explicitly stated why it was necessary to move away from Cavilieri's idea of dividing a line into points, a plane into lines, and so on. Wallis dealt with a line that was 'dilutable', having just enough thickness so that by collecting an infinite number of them together it would make up the required size of plane.
- This insight would lead directly to Newton's development of calculus.
- Gottfried Wilhelm Leibniz (1646-1716):
- The indivisibles that Leibniz worked with did have a measurable magnitude. They were infinitely small quantities that were defined by being smaller than any given quantity you would care to specify.
|
8. 極小量の謎:
- ジョン・ウォーリス:
- ∞の記号の発明者であり、極小量の理論を定式化し、線を点に、面を線になど分割することから脱皮することなぜ必要かを主張した。希薄化できる線を考え、それでも十分な幅があるので、無限数を集めれば必要な平面を作ることができるとした。
- この洞察は、ニュートンの微分法にも影響を与えた。
- ゴットフリート・ライプニッツ:
- ライプニッツが取り組んだ極小量は、大きな波紋を拡げた。それらは無限に小さな量で、どのように想定した数よりも小さい量として定義された。
|
>Top 9. Fluxion Wars:
- For something that was regarded as non-existent, infinity was capable of producing very real emotions.
- The first contender in the battle of the infinite was Isaac Newton, then 23 years old.
- Newton's ideas on gravity and planetary motion were developing well, he lacked the tools to be able to work properly on the numbers involved.
- As an apple dropped from the tree, how did its speed vary as it fell towards the ground? How could the movement of the planets in their orbits be predicted?
- Newton wanted to know what the acceleration was at any particular time. What was the elusive tangent for any point on the curve.
- He called it 0- a sort of misshapen zero that's not quite zero but just a little bit more.
- Define acceleration: t=time
- the change in speed: (t+0)2−(t)2
- the change in time: (t+0)−t
- So, the slope, or the acceleration is:
(t+0)2−t2(t+0)−t=2×t+0
- Newton termed his calculus 'the method of fluxions', where his fluxion was the rate of change of something.
- The business of dividing zero by zero has caused much confusion over the years.
- For Newton, his value 0 was in the process of being diluted.
- What was important in terms of calculus, was not what was but how it moved and changed - not the infinitesimal but the minuscule motion.
- Leibniz terminology:
- Using 0 inevitably caused confusion with zero, and did not indicate what it represents a small increment of.
- Leibniz's dx was much clearer: dxdy showing how x changed with respect to y.
- >Top In late 17C, Europe underwent a calculus revolution that had an impact on science and engineering similar to that of the late IT revolution, where once again a new technical capability would make what had been impossibly complex into something remarkably simple.
|
9.
流動戦争:
- 存在しないと思われていたものにとって、無限は現実の感情を呼び起こすことができる。
- 無限を巡る闘いの最初の挑戦者は当時23歳のアイザック・ニュートンだった。
- ニュートンの重力や惑星の動きに関するアイデアはうまく展開できていたが、それを数量化する道具に欠けていた。
- リンゴが木から落下する、その際に地面に向かってその速度はどのように変化するのか。衛星の軌道上の動きをどのように予測するのか。
- 特定の時刻における加速度はどのようにしてわかるのか。曲線上にある点での接線をどのようにして求めるのか。
- 彼はそれを、全くの0ではなくそれよりほんの少し大きなゆがんだゼロとして0で表現した。
- 加速度の定義: t=timeとすると
- 速度の変化: (t+0)2−(t)2
- 時間の変化: (t+0)−t
- 従って、傾き、即ち、加速度は:
(t+0)2−t2(t+0)−t=2×t+0
- ニュートンはこの計算法を'流動法'と呼んだ。流動とは何かの変化率をいう。
- ゼロをゼロで割ることに対しては、何年もの間混乱を生じてきた。
- ニュートンにとって、0の値は薄められていく過程のことである。
- 計算法にとって重要なのは、それが何であるかyほりも、どのように動き、変化していくかである。微少量がどうかではなく、微小な動きはどうかである。
- ライプニッツの記法:
- 0を使うことは、必然的にゼロとの混乱を生じた、また微小な増分は何を示しているかは明確でなかった。
- その点、ライプニッツのdxの記法は明確だった。dxdyはyに対するxの変化率を示す。
- 17C末は、欧州では、科学技術に対する"微分革命"がに進行した。あたかもIT革命のように。それは複雑すぎると思われていたことが画期的に単純になるような新たな技術能力の登場であった。
|
>Top 10. Paradoxes of the Infinite:
- Bermard Placid us Joann Napalmed Bolzano (1781-1848):
- His ability to challenge accepted wisdom and come up with startling new ideas, a tendency that is often punished rather than rewarded.
- In 1805, still 24, awarded the chair of philosophy of religion; ordained a priest.
- He wrote Paradoxes of the Infinite. Catholic Church had charged him with heresy.
- Bolzano's two approaches to infinity:
- a sequence of whole numbers, saying that as it can't conceivably be said to have a last term. Let's give a name to that last number 'ultimate', when what's wrong with ultimate+1? Also a whole number?
- He considers the true infinity to be found only in God, the absolute. It is the basis for a substandard infinity that merely reaches towards the absolute, but never reaches it. He calls this form of potential infinity.
- Often in calculus as small as we need it to be without ever reaching the absolute, ultimate, truly infinite.
- After years; infinity was just this virtual destination of a variable factor.
- His great successor Georg Cantor was to build the picture of the true infinity that we still use today.
- Not only did Bolzano consider the simple sequence 1, 2, 3, ..., he also looked at the harder to pin down concept of every single number (all the fractions) between 0 and 1.
- π: The range of fractions between 0 and 1 gaps open like a huge chasm - the closer you get to it, the more detail you are aware just how little of the detail you can actually comprehend.
- >Top In the case of all the fractions between 0 and 1, there was a one-to-one correspondence with the infinity of fractions between 0 and 2. He did this using a function, a mathematical black box that turns one thing into another.
- In effect, a function is a mathematical computer, an imaginary box that turns an input number into an output.
- In the early 1800s, Bolzano's words were little short of treason. In 1819, Bolzano was dismissed from his position.
- He spent 28 years retired, working on a wide range of subjects from mathematics to linguistics.
- Bernhard Riemann concentrated on on the way series and analytical tools like calculus could make use of infinity in order to safely reach results.
- Georg Cantor, who could put infinity squarely on the mathematical map.
|
10.
無限のパラドックス:
- Bernard Bolzano:
- 当時の定説に反抗し、新アイデアを提出し、称賛よりも批判された。
- 1805年24歳の時に宗教哲学を修め司祭となる。
- 彼の無限へのアプローチは2案あった。
- 整数の連続。最終項は示せないので、無限となるか。もしそれを「無限」と呼ぶと、無限+1も整数として存在する。
- 新の無限は絶対神の中にある。それはその絶対に近づく無限が基礎となる。これを「可能な無限」と呼ぶ。
- 微分では、それは必要な限りなく微小な数で、絶対的究極的な真の無限には決して到達はできないものの限りなく微小な数として扱う。
- 後年になって、無限はまさに変化していく数の仮想的な方向であった。
- 彼の偉大な後継者となるGeorg Cantorは、今日使用される真の無限の概念を確立することになる。
- 彼は、1, 2, 3, ...と続く整数だけでなく、0と1の間の分数にも着目した。
- π: 0と1の間の分数には大きな隙間がある。それに接近すればするほど、実際にはほんの少ししか知り得ていないことに気づく。
- 0と1の間の全ての分数は、0と2との間の全ての分数と1対1の関係がある。彼は、数学でいう1つの物から他の物へ転換するブラックボックである「函数」を使ったのだ。
- 実際に、函数は数学のコンピュータであって、入力を出力に変換する仮想の箱(函)である。
- 1800年代初期には、Bolzanoの主張は反逆そのものであった。1819年には役職を追放される。
- その後28年間の引退生活を送るが、数学から言語学の後半なテーマに取り組む。
- Berhard Riemannは微分の分析手法に集中し成果を残す。
- Georg Cantorも無限と正面から取り組み、数学上の地図を残す。
|
>Top 11. Set in Stone:
- Georg F. Cantor (1845-1918): Set theory:
- Set theory relies on there being something called the empty set. A set of nothingness. Although it may seem obvious, we start by defining zero as being this empty set.
- We can then produce the rest of the counting numbers by effectively adding a new set for every number, each enclosing the previous one like a set of containers.
- 0: ∅; the empty set:
- 1: {∅}; the set containing one set (the empty set)
- 2: {∅, {∅}}; the set containing two sets (the empty set, and the set containing the empty set)
- 3: {∅, {∅}, {∅, {∅}}}; the set containing three sets (the empty set, the set containing the empty set, and the set that contains the empty set and the set containing the empty set)
- >Top Cantor's set theory lies at the heart of mathematics. As sets were further explored, it seemed impossible to use them without encountering paradoxes.
- >Top Bertrand Russel (1872-1970): Russel's Paradox
- Russel too all the sets that are not members of themselves. Think of the whole set of these sets - the set of 'sets that aren't members of themselves'. Is this set a member of itself?
- <Russell's paradox>
You will probably need to reread that; is the set 'sets that aren't members of themselves' a member of itself?
- If it is a member, then it's a set that isn't a member of itself - so it isn't a member. If it isn't a member, then it's not a 'set that isn't a member of itself'
- This careful dissection of definitions shows a contradiction at the very heart of the nature of sets.
|
11.
もはや変えられない:
- 集合論
- 集合論の最初は、空集合を考える。
- 数字に対応した集合を作成、1つ前の集合を含む新たな集合を考える。
- 0: ∅; the empty set:
- 1: {∅}; the set containing one set (the empty set)
- 2: {∅, {∅}}; the set containing two sets (the empty set, and the set containing the epty set)
- 3: {∅, {∅}, {∅, {∅}}}; the set conting three set (the empty set, the set containing the emtpy set, and the set that contains the empty set and the set containing the empty set)
- カントールの集合論は、数学の中心にある。さまざまな集合を考慮すると、矛盾を含む集合がある。
- バートランド・ラッセル:
- <ラッセルのパラドックス>
自分自身をその要素として含まない集合のすべての集合(A集合)を考える。(それ以外はB集合)
- もしそれがA集合に含まれるとすると、それは自分自身をその要として含まない条件に反するので、B集合に属することになる。
- もしそれがB集合に含まれるとすると、B集合は、自分を含まない集合という定義に反する。
|
>Top 12. Thinking the unthinkable:
- Georg Cantor's set theory opened up a gateway.
- Cantor himself was to suffer for his dalliance with the infinite, and he was not to be the last great mathematician to have his mind damaged by the attempt to handle such an impossible concept. The constant effort to encompass the unthinkable must have had an insidious impact on the man's mind.
- To distinguish this real infinity from the virtual fuzziness of potential infinity∞, Cantor gave it a new symbol ℵ:
- For the sort of infinity that contains all of the natural counting numbers he used the name ℵ0, pronounced aleph-zero, or aleph-null.
- Aleph is the first letter of Hebrew alphabet.
- Also related to Jewish mystical tradition, 'cabbala', one of the representations of God as the infinite was aleph.
- Add 1 to ℵ0 and you get ℵ0.
- Similarly ℵ0+ℵ0 = ℵ0, and perhaps most strangely of all, ℵ0×ℵ0 = ℵ0
- >Top the squares and cubes should be as numerous as the totality of the natural numbers because both of these are as numerous as their roots, which constitute the totality of the natural numbers. (one-to-one correspondence, or bijection)
- Cantor was saying that an infinite set will have the same 'cardinality' as a subset of itself.
|
12.
想像を絶することを考える
- ゲオルグ・カントール (1845-1918) :
カントールの集合論はゲートウェイを切り開いた。
- カントール自身は無限の問題に取り付かれ精神を病んだ。
- 想像を絶することを対象に努力し続けたことも、精神の失調を生じた。
- 曖昧な概念である無限∞の記号とは異なる記号ℵを導入しリアルな無限を区別した。
- すべての自然数を含む無限として、ℵ0を導入した。
- ℵ
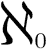 はヘブライ語の最初の文字 はヘブライ語の最初の文字
- ユダヤ教の神秘的な伝統の'カバラ'
- ℵ0に1を加えてもℵ0
- 同様に、ℵ0+ℵ0 = ℵ0であり、驚くべきことに、ℵ0×ℵ0 = ℵ0でもある。
- 平面や立体には自然数を沢山含まれているように思えるが、それらは自然数の根として対応できる。 (1対1対応、全単射)
- カントール曰く、無限集合はその部分集合と同じ濃度を持つ。
|
>Top 13. Order versus the Cardinals:
- A simple familiar symbol like 7 could represent both the integer 7 and the property of the appropriate set that we call its cardinality, meaning:
- Integer: seven
- Cardinal number: a set of seven; number denoting quantity (<L. cardo=hinge)
- Ordinal number: seventh; non-negative integers, ordinal 7 is define as {0, 1, 2, 3, 4, 5, 6}
- Cardinality is defined by one-to-one correspondence, making it reasonable for ℵ0 +1 to be the same as ℵ0. (Things are rather different with the ordinals.)
- >Top Having reached infinity, there still has to be a 'next one'. And so for the ordinals a new symbol for the 'smallest ordinal infinity' was devised. (ω) (< the Alpha and the Omega); the first transfinite ordinal, but it is then followed by ω+1, ω+2, ...
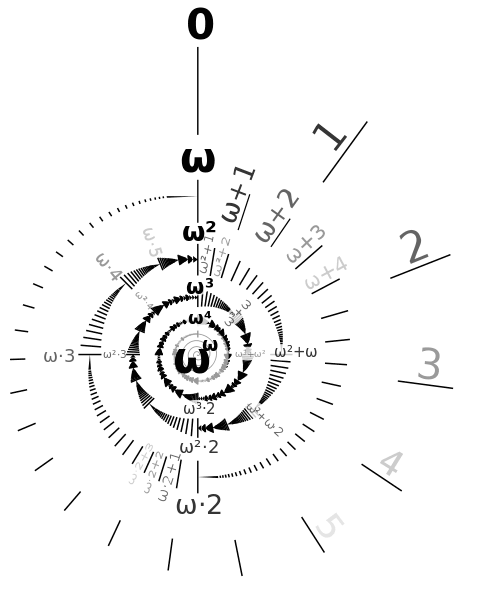 The ordinal number of a finite set will be the same as its cardinal number. But once we get to infinity and beyond (called transfinite numbers) we need to make the distinction. The ordinal number of a finite set will be the same as its cardinal number. But once we get to infinity and beyond (called transfinite numbers) we need to make the distinction.
- The ordinal number of the set {a1, a2, a3, ...} is ω, but that of {a2, a3, ..., a1} is ω+1.
- Thus, ω+2 is not the same as 2+ω, and 2×ω is not the same as ω×2.
- This means of combining results produces infinite ordinals which go up through an increasing scale ω+1, ω+2, and so on, until they reach ω×2, which is the ordinal of the set {1, 2, 3, ...; ω, ω+1, ω+2, ...}.
- After working ω×2, ω×3, and so one, we get another infinite series reaching ω×ω, or ω2.
- Carrying on in this fashion we can reach ωω, and from there (ωω)ω, and so on, until the sequence of ω powers stretches up like an infinite kite-string.
- The new ordinal is given the label ∈0 as the new starting point. Here we start all over again with ∈+1, ∈+2, and so on, forever.
- Cantor's infinite ordinals showed that it was possible to go on in a structure, an ordered, way beyond infinity when we are consider order.
|
13.
序数対基数:
- 数字7の意味
- 整数としての7
- 基数としての7; 7つの集合。
- 序数としての7; 7番目
- 基数は、1対1対応で定義される。ℵ0+1はℵ0と同じ。
- 無限に到達すると、その次の段階がある。最小序数の無限 (=最小超限序数)をωで表す。それはω, ω+1と続く。
- 有限数であれば、序数と基数は一致するが、超限数では区別する必要がある。
- {a1, a2, a3, .. }の集合の序数はωであるが、{a2, a3, ..., a1} の集合の基数は ω+1である。
- 同様に、ω+2と2+ωとは異なり、2×ωとω×2も異なる。
- このように無限の序数と組み合わせることでω+1, ω+2と無限序数を作ることができ、それはω×2に至る。つまり{1, 2, 3, ...; ω, ω+1, ω+2, ...}の集合である。
- ω×2, ω×3の後、次ぎの無限の列 ω×ω, or ω2が続く。
- これを繰り返すことで、ωωに至り、さらに(ω^ω)^ωとなる。ωの列は無限の凧の糸のように続く。
- そしてなんと、さらに新たな序数∈0が定義され、それが出発点となり、∈+1, ∈+2と無限に続く。
- カントールの無限序数は階層化しており、無限の先にも秩序がある。
- 注)
- >Top 無限は、涅槃(nirvana)の世界
- 無限序数は恒河沙もあり、ωは彼岸の観音, ω×2は菩薩, ω×ωは如来, (ωω)ωは釈迦如来と考えるとわかりやすい。また有限・無限は、仏教でいう二辺か。
|
>Top14. An Infinity of Infinities:
- Denumerable or countably infinite; sounds something of an oxymoron. If something is infinite, by definition it can't be counted. You will never reach an end, but the process is possible.
- Cantor arranged all the rational numbers in a number square. From the left to right the top number of the ratio gets bigger, from top to down the bottom number of the ratio get bigger. This infinite square would in theory include every single rational number. There's a lot of repetition in here. But this doesn't matter.
- The rationals have the same cardinality of ℵ0.
- Number square of rational numbers:
-
| 1/1 |
2/1 |
3/1 |
4/1 |
5/1 |
6/1 |
7/1 |
8/1 |
9/1 |
10/1 |
... |
| 1/2 |
2/2 |
3/2 |
4/2 |
5/2 |
6/2 |
7/2 |
8/2 |
9/2 |
10/2 |
... |
| 1/3 |
2/3 |
3/3 |
4/3 |
5/3 |
6/3 |
7/3 |
8/3 |
9/3 |
10/3 |
... |
| 1/4 |
2/4 |
3/4 |
4/4 |
5/4 |
6/4 |
7/4 |
8/4 |
9/4 |
10/4 |
... |
| ... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
- In 1873, Cantor found a way to work through a sequence of these numbers just as he had in the number square of the rationals (the diagonal argument)
- He imagined a sequence of every number (rationals and irrationals) between 0 and 1. Here there is only one, infinitely tall column.
- All numbers between 0 and 1:
-
| 0 |
| ... |
| 0.4382021757328058392048230 ... |
| ,,, |
| 0.7320342848341748399219484 ... |
| ... |
| 1 |
- What Cantor did was to imagine going down his table, taking the first digit from the first number, the second digit from the second number, the third digit from the third number, and so on, all the way through the whole sequence. Next he changed every digit in this new number (For example, add 1 to every digit (shifting 9 up to 0).
- It is different from every single number in the table.
- It's an unavoidable fact - you can't make a one-to-one matching of every single number, rational and irrational, between 0 and 1 with the counting numbers. After we've gone through the whole column, there are still numbers left over. There are more numbers between 0 and 1 than there are integers. There are different kinds of infinity.
- The cardinality of the numbers between 0 and 1 fitted into a larger 'dimension' than ℵ0, presumably one of the greater alephs (or even something in between levels), but he had not proved that it had the value ℵ1.
- >Top 'The continuum hypothesis'; the cardinality of the above rational and irrational number was ℵ1.
- Cantor moved up form the one-dimensional number line of 0 to 1, to a two-dimensional square.
- He wold transform the pairs of coordinates into a list of single numbers. All he had to do was alternate digits between the first and second coordinates that provided the location of a point on his square. If the numbers happed to be
0.3302829492 ... and 0.7347272901 ...
his new number would be 0.37330427822792949021 ...
- The single number contains all the information that was in the other two. And this was no different to the list of numbers that mapped out the line. It was at exactly the same level of infinity. It had the same cardinality.
- What he had proved was the one-dimensional space has exactly the same number of points as does two dimensions, or three dimensional space or as many dimensions as you like.
- Richard Dedekind said, "I see it but I don't believe it."
- Galileo had effectively proved that ℵ0×ℵ0=ℵ0
- What Cantor had now shown was that ℵ? × ℵ? = ℵ?
- Cantor discovered that the continuum (or c for short) itself is the power set of the integers. This made the greater infinity which might or might not be ℵ1 to be 2ℵ0.
- He had opened up one more fact about these special numbers that were infinity and more, the transfinite numbers. While adding or multiplying infinities didn't move up a level of complexity, multiplying a number by itself an infinity number of times did.
- Let's use the binary system: Once we've written all the numbers in our infinite table in this binary system form, we find each number has aleph-null digits. Whenever there's a set of thing that can have two values, the number of combination is 2n, the good old power set. So we have in this case 2ℵ0 possible numbers.
- I would seem all too sensible that the next level of infinity, the infinity of the continuum, should be ℵ1 (But Cantor could not prove this, but he believed it was so.)
|
14.
無限大の無限大:
- 可算(可付番)無限は、矛盾に聞こえるかもしれない。無限の定義は数えられないということだから。その最終には到達できないが、そのプロセスは可能である。
- カントールはすべての有理数を数の四角に整理した。 (左表)。列の左から右へ分子の数が増えていき、行の上から下へ分母の数が増えている。この表には重複は沢山あるが、すべての有理数が記載されている。
- 有理数の基数はℵ0である
- 1873年に、カントールはこの有理数の表に一連で並べられることを発見した。
- 彼は、0と1の間にある一連の有理数と無理数の列を想定した。(左表)
- カントールが行ったのは、1行目の数から1桁目を取り、二行目の数からは2桁目というように採番した。次ぎに、その全ての桁の数字を、1を足すことで変える。9は0にする。
- その数字は、この表にあるどの数字とも異なる。
- すなわち、0と1の間にあるすべての有理数と無理数は可付番ではないことが判明した。この表の最後まで言っても、まだ数字が残っていることになる。つまり、0と1の間にはすべての整数より多くの数がある。それは異なる次元の無限である。
- 0と1の間の基数の数はℵ0より大きな次元をもつことになる。つまりℵ1となるのが予測されたが、カントールはまだそれを証明していない。
- 連続体仮説:上記の有理数と無理数の基数はℵ1であるとする仮説。
- カントールは、0と1の間の1次元の数から、2次元数へと拡張した。2つの座標軸から成る数を考える。そして、これらの数の桁を順に交互に取り出して新たな数を作る。
例えば、0.3302829492 ... と 0.7347272901 ...から、
新しい数字 0.37330427822792949021 ... を作る。この新しい数字には、前の2つの数字の情報がすべて含まれ、これは1次元の場合の数と全く同じになる。即ち、基数は同じとなり、無限の濃度は同じということになる。
- この論理は、2次元のみならず、3次元、多次元でも成り立つ。
- R. デデキント曰く、"理解できるが信じられない!"
- ガリレオは実質的に、ℵ0 × ℵ0 = ℵ0を証明した。
- カントールは、 ℵ? × ℵ? = ℵ?を証明したことになる。
- カントールは、連続体仮説 (cと略称するが)は、整数のべき乗であることを示した。より大きな無限が、ℵ1であるか2ℵ0であるかを示した。
- 彼はさらに、無限の先に超限数があることを発見した。無限の数は足しても掛けても、その複雑性は変わらないが、それ自身の無限を掛けると無限のレベルが変化する。
- 二進法でやってみる。すべての無限テーブルを二進法で書き直すと各数字はℵ0桁となる。2値をとる数の組合せの数は2nとなる。無限テーブルでは、これが2ℵ0となる。
- 次のレベルの無限とはℵ1となることが予想されるが、カントールはまだこれを証明していないが、そうなると信じている。
|
>Top 15. Madness and Sanity:
- Where Kurt Gödel (1906-1978) had shown that there was no contradiction between the continuum hypothesis and set theory, Paul Cohen (1934-2007) managed to prove that set theory would still work if the continuum hypothesis was untrue.
- >Top Axioms are mathematics' givens - the assumptions that are made to begin with. (The Zermelo-Frankel axioms) , particularly,
- The axiom of choice - for every set we can provide a mechanism for choosing one member of any non-empty subset of the set.
- The axiom of choice and the continuum hypothesis are all part of the same mathematical structure, but there is no relationship between them and there rest of the axioms; they are entirely independent.
- As long as we continue to use these axioms as the givens, the things we take for granted about sets, then there can be no progress made on the continuum hypothesis.
- God exists since mathematics is consistent, and the devil exist since we cannot prove it.
|
15.
狂気と正気:
- クルト・ゲーデルは、連続体仮説と集合理論との間に矛盾はないことを示している点で、ポール・コーエンは、連続体仮説が真でないとしても集合論は成り立つとした。
- 数学の公理とは、数学が成り立つための前提。(ツェルメロ・フレンケルの集合論に関する公理)、特に
- 選択の公理 (ChoiceのCを加えたZFC): Xが互いに交わらないような空でない集合の集合であるとき、Xの要素から一つずつ要素を取ってきたような集合が存在する。
- 選択の公理と連束体仮説とは同じ、数学的な構造を持つ。但しそれらやその他の公理との間に直接の関係はない。それらは完全に独立している。
- これらの公理を当然のこととして受け入れると連続体仮説についての進歩はなくなる。
- 数学は、無矛盾であれば、神が存在し、無矛盾を証明できなければ悪魔が存在する。
|
>Top Cf: Continuum hypothesis (CH):
- There is no set whose cardinality is strictly between that of integers and that of the real numbers.
- Intuitively, there are ore rational numbers than integers, and more real numbers than rational numbers. However, it turns out the rational numbers can actually be placed in one-to-one correspondence with the integer, therefore the set of rational numbers is the same size (cardinality) as the set of integers.
- Cantor gave proofs that cardinality of the set of integers are smaller than that of the set of real numbers.
- However, his proof give no indication of the extent to which the cardinality of the integers is less than that of the real numbers.
- Cantor proposed the continuum hypothesis as a possible solution to this question.
- The CH states that the set of real numbers has minimal possible cardinality which is greater than the cardinality of the set of integers.
- The cardinality of the integers is ℵ0 ("aleph-naught") and the cardinality of the real number is 2ℵ0, the CH says that there is not set S for which
ℵ0<|S|<2ℵ0
- Assuming the axiom of choice, there is a smallest cardinal number ℵ1 greater than ℵ0, and the CH is equivalent to:
2ℵ0=ℵ1
- Generalization of CH (=GCH) says that for all ordinals α
2ℵα=ℵα+1
- A consequence of CH is that every infinite subset of the real numbers either has the same cardinality as the integers or the same cardinality as the entire set of the reals.
|
連続体仮説(CH):
- 直感的には、整数より有理数が多く、有理数よう実数が多い。しかし、有理数の集合は、整数の集合と1対1対応ができるので、それらのサイズ (濃度)は等しい。
- カントールは、整数の集合の濃度は、実数の集合のより小さいことを証明した。
- 但し、彼の証明ではどの位小さいのかを示さなかった。
- カントールは、この疑問に対し"連続体仮説" (CH)を提唱した。(連続体=実数)
- CH曰く、実数の集合は、整数の集合の濃度より大きい最小の可能なの濃度を持つ。
- 整数の濃度をℵ0とすると、実数の濃度は2ℵ0となり、CH曰く、この間に入る濃度はない。
- "選択の公理"を前提とすると、ℵ0より大きい濃度はℵ1であり、CHでは、2ℵ0=ℵ1と主張する。
- これを一般化すると、すべての濃度αにたいして、2ℵα=ℵα+1が成り立つ。
- CHの結論として、実数のどの無限の部分集合は、整数の濃度と同じか、または全実数の集合と同じ濃度となる。(任意の実数の部分集合は、整数の集合との間に全単射が存在するか、実数の集合との間に存在するかのいずれか)
|
>Top 16. Infinitesimally Small:
- It's hard to get as exited about the opposite end of the number size spectrum - the incredibly small.
- If you divided 1 by infinity is 0, but is infinitesimal?
- Leibniz went on to clarify as being 'as small as you please.'
- George Berkely, philosopher refers to infinitesimals as ghosts of departed quantities.
- Imagine the smallest number there could be - call it ghost. Now divide it by 2. We've just produced a number that is bigger than zero, yet is smaller than ghost. So ghost wasn't the smallest number there could be
- We know that ℵ0×2=ℵ0, so why should it not be the case that ghost2 = ghost?
- Abaraham Robinson (1918-1974):
- In essence, the original idea was recognizing that infinitesimals were outside the standard number system - that jut like imaginary numbers they operated in something akin to a different dimension.
- It was no more meaningful to say that an infinitesimal was between the smallest 'real' number and zero than to try to fit i, the square root of -1.
- And just like the complex number that has real an imaginary components, there could be a complex number with standard and non-standard components. Newton's 2x+0 is a classic example of this - 2x being the standard component, and o the non-standard.
|
16.
無限小について:
- 考えられないような極小の数をイメージすることは難しい。
- 1を無限大で割ると0になるが、それが極小値か。
- ライプニッツは、極小値とは好きなだけ小さな数とした。
- 哲学者のG. バークレイは、極小値とは死んだ数の幽霊のようだと表した。
- 極小値を想定して、それを幽霊と呼ぼう。それを2で割ると、ゼロよりは大きいが、幽霊よりは小さくなるはずだ。だが、幽霊は最も小さな数としたいはずだ。
- 我々は、ℵ0×2=ℵ0であることを知っている。では、幽霊2=幽霊となるのか。
- エイブラハム・ロビンソン:
- 当初のアイデアとしえ、極小値は標準の数とは別のものとして認識された。あたかも虚数のように異なる次元にある。
- むしろ極小値を最小値とゼロの間の数とするより、虚数iのような扱いをしてはどうか。
- つまり複素数のように、標準的な数と、非標準の数の組合せとして扱うのである。ニュートンのいう2x+0は、この古典的な例であって、2xは標準数、0は非標準数とするのである。
|
>Top 17. Infinity to Go:
- "Only two thing are infinite, the universe and human stupidity, and I'm not sure about the former." (Albert Einstein, 1930s)
- Many of the great mathematicians of history have been most comfortable in this abstract universe, where the important thing is not to find a practical use for a theory but to discover effective and elegant methods with which theorems and proofs are slotted into place.
- At the other extreme is real mathematics, the mathematics that would best suit Cantor's nemesis, Leopold Kronecker, where every mathematical concept has to be grounded physical reality.
- >Top Fractals:
- One field of modern mathematics that seems to open up the boundaries for infinitesimal space in the real world is fractals. This fascinating adjunct to chaos theory demonstrates quite painless that it is possible in principle to have something infinitely long drawn in normal, finite space.
- Helge von Koch (1870-1924), Swedish mathematician:
- Koch curve, 1906:
Each of the three sides of the original triangle is extended be made up of four segments, each 13 the length of the original line - so the length of each of the three sides is now 43 of what it was.
- Koch now went on to perform the same 13 side triangle addition to each of the smaller subsides. So now each of these is 43 longer. And this process is repeated forever. The sides get longer and longer, becoming infinitely long, but the shape rather like a crinkly snowflake, does not grow beyond the bounds of a circle drawn around the original triangle.
- Fractal dimension:
A fractal line measured at first to be one length, when remeasured using a new stick scaled by 13 of the old is 4 times as many scaled sticks long. In this case, N=4 when ε=13, and the fractal dimension can be: D=limk→∞log4klog3k=log4log3≈1.262
- Fractals certainly allow us to envisage the possibility of infinity in a finite world.
- >Top Goldbach conjecture, 1900:
one of the oldest and unsolved problems in number theory. It states:
Every even integer greater than 2 can be expressed as the sum of two primes.
- The conjecture has been shown to be correct up through 41018 and is general assumed to be true, but no mathematical proof exists.
- Goldbach number: an even positive number that can be expressed as the sum of two primes.
- 2(2) = 4=2+2
- 2(3) = 6=3+3
- 2(4) = 8=3+5
- 2(5) =10=3+7=5+5; ...
- 2(50) =100 = 3+97=11+89=17+83=29+71=41+59=47+53 ...
- Although many mathematicians don't like it, computers can be used to disprove a conjecture like this. Such an approach can't prove that something is true, but if it ever finds a case where it's not true, the conjecture can be disposed of.
|
17.
身近な無限:
- 歴史上の多くの偉大な数学者は抽象世界に安住してきたが、そこで重要なのは実際的な理論を見つけることではなくていかにうまく美しい方法で定理や証明を発見するかだった。
- その対局にいる数学者がレオポルド・クロネッカーで、カントールの宿敵で、全ての数学的な概念は物理的な現実が必要であるとした。
- フラクタル:
- 現実世界に極小空間という境界を切り開いた現代数学の1分野がフラクタルである。こえはカオス理論と関連しており、有限の空間に無限の長さをもつことを可能にした。
- ヘルゲ・フォン・コッホ (スウェーデンの数学者, 1870-1924)
- コッホ曲線(1906)
元の三関係の各辺に、辺の長さの1/3の小三角形を追加すると、三辺の長さは4/3になる。その小三角形の辺にさらに小さな三角形を追加していくことを永遠に続ける。辺の長さはどんどん長くなり無限大となるが、形はしわしわの雪の結晶のようになり、元の三角形の外接円の境界を越えない。
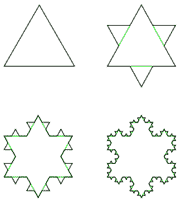 - フラクタル次元:
各操作で、1/3が4辺になるので、N=4、ε=1/3として、フラクタルの次元は以下で計算できる。
D=limk→∞log4klog3k=log4log3≈1.262
- フラクタルは有限の世界に無限の可能性を見せてくれる事例である。
- ゴールドバッハの予想:
整数論の未解決問題の一つとして、
"2より大きいのすべての偶数は、2つの素数の和で表すことができる。"
- これは、41018まで正しいことがコンピュータで求められているが、未だ数学的な証明はされていない。
- ゴールドバッハ数
- 2(2) = 4=2+2
- 2(3) = 6=3+3
- 2(4) = 8=3+5
- 2(5) =10=3+7=5+5; ...
- 2(50) =100 = 3+97=11+89=17+83=29+71=41+59=47+53 ...
- 多くの数学者は好きでないが、コンピュータはこのような予想の反証をすることができる。これはあることが真実であることの証明にはならないが、真実でないことがわかれば、その予想は破棄されることになる。
|
>Top 18. Endless fascination:
- Often, the boundaries between reality and infinity throw up paradoxical results, and it is these mind-teasing outcomes that give the study of the infinite a playfulness and fascination that lives on, however much we explore the philosophical, mathematical and theological implications of the subject.
- >Top Hilbert's paradox of the Grand Hotel:
- Hilbert imagine that a building with an infinite number of rooms, and the hotel is entirely full.
- Finitely many new guests:
A late arrival scramble into the foyer. Can they put him up? No problem. The occupant of Room-1 goes into Room-2, the resident of Room-2 into Room-3, and Room-n into Room-(n+1). Room-1 is vacated, but on one leaves.
- Infinitely many new guests:
Hilbert even imagines an infinitely large coach load of visitors arriving unexpected. The hotel doesn't have a problem. 1 goes to 2, 2 to 4, 3 to 6, and n to 2n. Suddenly all the odd numbered rooms - an infinity of them are available.
- Infinitely many coaches with infinitely many guests:
It is also possible.
First empty the odd numbered room as above, ten put the first coach's load in room 3n for n=1,2,3,..., the second coach's load in room 5n and so on; for coach number i we use the rooms pn were p is (i+1)-st. prime number.
- >Top Gabriel's horn:
- Gabriel's horn is formed by the graph of y=1x, with the domain (1≦ x<∞) and rotating it around the x-axis. (Solid of revolution and surface of revolution)
- Using integration the volume V=∫(1x2)dx=π(1−1/a)=π (because: lim a→inf)
- the surface S=2πln(a)=∞ (because lim a→∞)
- This means that the horn has an infinite surface though a finite volume (π).
- Imagine pouring a large can of paint into Gabriel's horn. After a while, the horn gets so narrow that the paint won't go any further. This is true whether you're pouring it in or painting the inside surface.
- In principle, if you tried to paint he outside of the horn you might need an infinite amount of paint but in practice again you would reach a point where the horn was too narrow for paint molecules to stick around the outside and coat it.
- Hilbert's hotel and Gabriel's horn illustrate why infinity is such a wonderful subject. Infinity is strange, powerful and outside our ability to fully comprehend, but it's also fun.
|
18. 無限につづく魅力:
- ヒルベルトの無限ホテル:
- 無限の部屋をもつホテルあり、それが満室とする。
- 有限の新規来客:
遅れて到着した新規客が1人いるとする。1号室の客を2 号室に、2号室の客を3号室へ、n号室の客をn+1号室へ順に移ってもらう。空いた1号室に新規客を入れる。新規客がn人の場合も同様。
- 無限の新規来客:
1号室の客を2号室へ、2号室の客を4号室へ、n号室の客を2n号室へ移動してもらう。奇数号室は空きになるので、無限の客を新たに泊めることができる。
- 無限の新規来客が無限大の数のバスで到着する場合:
まず上記のように奇数号室を空ける。1台目の乗客を3n (n=1, 2, 3, ...)号室に、2台目の乗客を5n (n=1, 2, 3, ...)号室に、i台目の乗客をpn (p=i+1番目の素数)に入れればよい。
- 加算無限集合の基数はℵ0と表される。
- ガブリエルのホルン:
 - y=1x(1≦x<∞)を、x軸の周りに回転して得られる回転体をを考えると、体積は有限 (π)だが、表面積は無限となる。
- このホルンにペンキを注ぐとどうなるか。ホルンは細くなるので、ペンキが中に入らなくなる。
- またペンキでホルンの外側を塗る場合はどうか。この場合も、ホルンがあまり細くなるので、ペンキの分子でさえうまく周囲を塗れなくなる。
- ヒルベルトのホテルも、ガプリエルのホルンも、無限がテーマである。無限は、奇妙で強力で、我々の理解を超えるが、それだけに興味深い。
|

 The ordinal number of a finite set will be the same as its cardinal number. But once we get to infinity and beyond (called transfinite numbers) we need to make the distinction.
The ordinal number of a finite set will be the same as its cardinal number. But once we get to infinity and beyond (called transfinite numbers) we need to make the distinction.

