化学者たちのパズルゲーム

おたっきーなNMRのページ

すべての始まり：なぜCOSYでスピン結合しているプロトンが分かるのか？

　COSYのパルス系列を見て考えた疑問がこれ。ベクトルモデルでいくら考えても分からない…。COSYのパルスシーケンスからベクトルモデルを考えると下のようになり、結論としては歪んだJ分解スペクトルのようなものしか得られないことになってしまいます。

　で、雑誌会で最新のNMRを紹介しようとしてふと実験化学講座を読んでいたらどのようにしてCOSYのスペクトルが得られてくるのか、この疑問の答えがのっていたわけです。結局のところベクトルモデルには限界があってCOSYのようなものでは適用できないということでした。で、これからそれをひっくるめていろんなNMRのブラックボックスな部分を解説してしまおうという恐ろしいページです。さあ、どのように暴走していくのでしょうか？（笑）というわけでマニアックなNMRのページです。でも役には立たないと思います（爆）。まあ、ちょっと読んでみて耐えられなさそうなら諦めてください…。

参考文献は主に次の3つ

「実験化学講座第四版　5　NMR」　丸善
…雑誌会で大変役に立った。ただし、パルス磁場勾配や3D-NMRはない時代の本。
「NMRの書」　荒田洋治　丸善
…雑誌会の時にはまだ出版されていなかった。この本があればよりマニアックになったのに。
「二次元NMR 原理と測定法」　吉岡書店
…原題はPrinciples of nuclear magnetic resonance in one and two dimensions（日本語タイトルは2次元しか扱っていないようで誤解を招くと思うが）。かのR. R. Ernst様 et al.が書かれた本。実は結構古かったり(1987)するが重要。ただしマニアックさは荒田様の本の上を行く。

化学のお部屋へ戻る

スピンの波動関数

　量子化学の講義で出てくる通り、Heitler-Londonの方法で水素分子の波動関数を考えるとき、2つの波動関数が得られます。1つは結合性軌道に対応するχ_A(1)χ_B(2)+χ_A(2)χ_B(1)というもので、もう1つは反結合性軌道に対応するχ_A(1)χ_B(2)-χ_A(2)χ_B(1)というやつです。ところが電子にはスピンというのがあってPauliの排他原理というのが効いてきます。(1)と(2)をすべて入れ替えたとき波動関数の符号が反対にならなければならないというやつです。スピンを含めた波動関数を考えると、Pauliの排他原理を満たすものとして

{α(1)β(2)-α(2)β(1)}{χ_A(1)χ_B(2)+χ_A(2)χ_B(1)}
{α(1)α(2)}{χ_A(1)χ_B(2)-χ_A(2)χ_B(1)}
{β(1)β(2)}{χ_A(1)χ_B(2)-χ_A(2)χ_B(1)}
{α(1)β(2)+α(2)β(1)}{χ_A(1)χ_B(2)-χ_A(2)χ_B(1)}

という4つが得られてきます。さて、ここでα(1)やβ(2)といったものが電子のスピンを表す波動関数です。原子核にもこのようなスピンが存在しています。これからやろうとしていることは、このスピンの波動関数が磁場やパルスによってどのように変化するのかを調べることです。これが分かればNMRがどのようにして観測されるのかが理解できるというわけです。

スピンと演算子

　まず最初にブラケット表記なるものについて説明します。例えば一次元の井戸型ポテンシャルの中の粒子について考えると井戸の幅がｘ軸方向に広がっている場合、波動関数はxの関数ψ(x)になります。一方、y軸方向に広がっていればyの関数ψ(y)に、z軸方向に広がっていればzの関数ψ(z)になります。このように同じ井戸型ポテンシャルを考えても座標軸の採り方で波動関数の表記は変わってしまいます。本質が変わりないのに表記がいくつもあるのは議論の上で不便なので、座標に関係無い抽象的な表記をします。これが状態ケット|ψ>というものです。（ただし、NMRにおいては主磁場の方向をz軸にとるという暗黙の了解があるので状態ケットと波動関数の表現はほとんど一対一に対応しますから状態ケット≒波動関数と考えても差し支えないような気も…）

　スピン1/2の核について、αスピン、βスピンを表すケットをそれぞれ|+>、|->と表記します。スピンは角運動量ですから、スピン角運動量のx成分、y成分、z成分の演算子をそれぞれIx、Iy、Izとすれば、Iz、スピン角運動量の大きさの演算子I²= Ix²+Iy²+Iz²、昇降演算子I₊=Ix+iIy、I_-=Ix-iIy、恒等演算子Eに対して

Iz|+> = 1/2|+>、Iz|-> = -1/2|->
I²|+> = 1/2(1+1/2)|+>、I²|-> = 1/2(1+1/2)|->
I₊|+> = 0、I₊|-> = |+>
I_-|+> = |->、I_-|-> = 0
E|+> = |+>、E|-> = |->

が成立します。（水素原子の波動関数ψにおいてI²ψ = l(l+1)ψ、Izψ = m_lψが成立することを思い出しましょう。ただし lは角運動量量子数：s軌道で0、p軌道で1、d軌道で2…、 m_lは磁気量子数で-lから+lまでの整数。）昇降演算子は|+>に作用して|->に変えたり、その逆を行ったりする演算子でNMRのパルスによるスピンの挙動を表しています。

　エネルギーの演算子はSchrödingerの方程式でお馴染みのハミルトニアンHで、z軸方向へかけられた静磁場B₀中におけるハミルトニアンはH = -γB₀(h/2π)Iz = -(h/2π)ω₀Izとなります。ω₀ = γB₀はLarmor（角）周波数です。H|+> = -1/2(h/2π)ω₀|+>、H|-> = 1/2(h/2π)ω₀|->であり、|+>が-1/2(h/2π)ω₀、|->が1/2(h/2π)ω₀というエネルギー準位に対応することが分かります。なお、NMRについてはエネルギーを角周波数単位[rad/s]で表すことが多く、この場合には(h/2π)を省略することができます（以下このページでもそのように扱います）。

　またケット|+>、|->に対してそれぞれブラ<+|、<-|を定義します。これは波動関数ψにおいては、その複素共役ψ^*にあたるものです。そして∫ψψ^*dτと同じ性質を持つものとして内積<A|B>を<+|+> = 1、<-|-> = 1、<+|-> = <-|+> = 0となるように定義します（実際には必ずしも∫ψψ^*dτ = 1にならないのと同様に、<+|+> = 1になるとは限りません。ただし<+|+> = 1となるように|+>に係数cを掛けて新しい|+>とすることが許されています。これをψの場合と同じように規格化といいます。）

　ここでI₊を|+><-|とおきます（このような|A><B|のような形式を外積といいます）。するとI₊|+> = |+><-|+> = |+>0 = 0、I₊|-> = |+><-|-> = |+>1 = |+>となり、ちょうど上で挙げた演算子の挙動と一致します。同じようにして他の演算子も

Ix = 1/2 (|+><-| + |-><+|)
Iy = 1/2i (|+><-| - |-><+|)
Iz = 1/2 (|+><+| - |-><-|)
I²= 3/4 (|+><+| + |-><-|)
I₊ = |+><-|
I_- = |-><+|
E = |+><+| + |-><-|

と外積によって表すことができます。

なお、上で出てきた数式はベクトルと行列を使って表記することもできます。この場合は次のようになります。外積の形式で表した演算子の|+><+|の係数が(1,1)成分、|+><-|の係数が(2,1)成分、|-><+|の係数が(1,2)成分、|-><-|の係数が(2,2)成分になっていることが分かります。

\|+>	\|->	<+\|		<-\|		Ix		Iy		Iz		I²		I₊		*I_-*		E
1	0	1	0	0	1	0	1/2	0	1/2i	1/2	0	3/4	0	0	1	0	0	1	0
0	1	1	0	0	1	1/2	0	-1/2i	0	0	-1/2	0	3/4	0	0	1	0	0	1

　また、任意のスピン|ψ>のオブザーバブルΩの期待値<Ω>は、それに対応する演算子をΩとすれば<Ω> = <ψ|Ω|ψ>となります（ちょうど電子の波動関数ψにおける<Ω> = ∫ψ^*Ωψdτに対応しています）。これを計算するのには上の行列表示が便利です。

Schrödingerの方程式

　Schr&#ouml;dingerの方程式はH|ψ> = i(d|ψ>/dt)　であり、ハミルトニアンHにtが含まれないとき（tとそれ以外の変数分離ができるので）、この解は|ψ>= e^-i^H^t|ψ₀>となります。例えばz軸方向へかけられた静磁場B₀中（H = -ω₀Iz）において、 e^-i^H^tの行列表示は

e^-i^H^t
e^iω0t/2	0
0	e^-iω0t/2

　この場合、スピンの角運動量の各成分の期待値は

<Ix> = < ψ|Ix|ψ> = 1/2 ( e^-iω0t/2+e^iω0t/2) = 1/2 cosω₀t
<Iy> = < ψ|Iy|ψ> = 1/2i ( e^-iω0t/2-e^iω0t/2) = -1/2 sinω₀t
<Iz> = < ψ|Iz|ψ> = 1/2 (1/2- 1/2) = 0

となります。<Ix>、<Iy>を見るとスピンがLarmor周波数で回転しているのが分かります。

密度演算子と密度行列

　ここまではただ1つのスピンを持つ核について考えてきました。しかし、NMRにおいてはただ1つのスピンを観察しているわけではありません。試料中に含まれるたくさんのスピンの挙動の総和を観察しているわけです。独立な多数のスピンが存在している場合、オブザーバブルωの期待値<ω>は、スピンがいくつかの状態|ψ_i> = c_i+|+> + c_i-|->で存在していて、それぞれの状態がw_iという確率で占められるとき、<ω> = Σw_i<ψ_i|ω|ψ_i>となります。(本当のところは、この式は1つのスピンが状態|ψ_i>をw_iという確率で占めるときの式で、これを多数のスピンに拡張しても同じように成り立つかはちゃんと別に示す必要があったりしますが…）

ρ
Σw_ic_i+c_i+^*	Σw_i c_i+c_i-^*
Σw_ic_i-c_i+^*	Σw_ic_i-c_i-^*

となります。これを密度行列といいます。密度行列を使用すると便利な点は、オブザーバブルωの期待値<ω> = Tr{ρω}と表すことができる点です。ただしTr{A}は行列Aの対角和(トレース）です。

　例えば、静磁場がない場合、スピンは|ψ> = |+>または|->という状態に確率1/2で等しく存在しています。このとき<Iz> = Σw< ψ|Iz|ψ> = 0です（|ψ> = |+>ならば< ψ|Iz|ψ> = 1/2、|ψ> = |->ならば< ψ|Iz|ψ> = -1/2でそれぞれが確率w = 1/2で占められているからです。）。このとき密度行列は

ρ		*ρIx*		*ρIy*		*ρIz*
1/2	0	0	1/2	0	1/2i	1/2	0
0	1/2	1/2	0	-1/2i	0	0	-1/2

となり<Ix> = 0+0=0、<Iy>=0+0=0、<Iz>=1/2+(-1/2)=0でいずれも0で磁化ベクトル<μ>= γ(h/2π)<I>も0です。

　また、全てのスピンが|ψ> = 1/2^1/2(|+> + |->)という状態にある場合（前の例との違いは、前の例では1つのスピンを取り出して観測した場合、何回測定しても状態が|+>か|->のどちらか片方だけが観測されるのに対し、この例では1つのスピンを取り出して観測した場合、|+>と|->がそれぞれ1/2の確率で観測されるところです。）密度行列は

ρ		*ρIx*		*ρIy*		*ρIz*
1/2	1/2	1/4	1/4	-1/4i	1/4i	1/4	-1/4
1/2	1/2	1/4	1/4	-1/4i	1/4i	1/4	-1/4

となるので、<Ix> = 1/4 + 1/4 = 1/2、<Iy> = -1/4i + 1/4i = 0、<Iz> = 1/4 + (-1/4) = 0となります。この状態はベクトルモデルでx軸方向へ磁化ベクトル<μ>= γ(h/2π)<I>が向いている状態に対応しているわけです。NMRのレシーバーは磁化ベクトル<μ>のx成分とy成分、つまり<Ix>と<Iy>に比例する部分を観測するので、この場合にはNMR信号が観測できることになるわけです。NMRは|->から|+>へスピンの状態が変化したのを観測しているといわれますが、これを見るとスピンの状態が|+>、|->が混じりあった状態になったのを観測しているという方が正確な感じです。

　前の例を拡張して全てのスピンが|ψ> = 1/2^1/2(|+> +e^iθ |->)という状態の例を考えます（前の例はθが0に相当）。この場合も前の例と同じように1つのスピンを取り出して観測した場合、|+>と|->がそれぞれ1/2の確率で観測されます。この場合密度行列は

ρ		*ρIx*		*ρIy*		*ρIz*
1/2	1/2e^-iθ	1/4 e^-iθ	1/4	-1/4ie^-iθ	1/4i	1/4	-1/4e^-iθ
1/2e^iθ	1/2	1/4	1/4 e^iθ	-1/4i	1/4ie^iθ	1/4e^iθ	-1/4

となるので、<Ix> = 1/4 e^-iθ + 1/4 e^iθ = 1/2cosθ、<Iy> = -1/4i e^-iθ + 1/4i e^iθ = 1/2sinθ、<Iz> = 1/4 + (-1/4) = 0となります。磁化ベクトルはxy平面内をx軸正方向からθだけ反時計回りに回転した方向を向いている状態です。後述するように静磁場中では時間とともにθが変化して磁化ベクトルがxy平面を回転するLarmor歳差運動が起こっています。

　一方、ここでスピンが|ψ> = 1/2^1/2(|+> +e^iθ |->)ですが、θは各スピンによってバラバラの任意の値をとっているという状態の例を考えます。この場合も1つのスピンを取り出して観測した場合、|+>と|->がそれぞれ1/2の確率で観測されます。θのバラツキに偏りがなければ、密度行列は上の例のθを任意の値に変えた場合の平均となります。e^iθおよびe^-iθのθを任意の値に変えた場合の平均値は0ですから

ρ		*ρIx*		*ρIy*		*ρIz*
1/2	0	0	1/4	0	1/4i	1/4	0
0	1/2	1/4	0	-1/4i	0	0	-1/4

となり、<Ix>=<Iy>=<Iz>=0で磁化は存在せず、NMR信号を観測することはできません。このように単に各スピンが|+> と|->が混じり合った状態にいるだけではNMRを観測することはできません。全部のスピンの状態の位相θがそろっていないとNMRは観測できません。この位相がそろった状態をコヒーレンスがあると言います。NMRはスピンのコヒーレンスを観測しています。

ベクトルモデルとの対応

　今までの部分で密度行列とベクトルモデルがどのように対応するのかを明らかにしてきました。次にベクトルモデルでの挙動と密度行列の挙動を対比していきます。

密度行列の時間変化

　前の例で取り扱った密度行列（密度演算子）は時間変化をしていませんでした。しかし、密度行列（密度演算子）を計算するもとになるスピンの波動関数はSchrödingerの方程式に従って時間変化をします。そのため密度行列（密度演算子）も時間変化をします。時間変化する密度演算子が満たす方程式はSchrödingerの方程式を変形して導出できdρ/dt = i(ρH-Hρ) = i[ρ,H] （交換演算子[ρ,H] = ρH-Hρ）となり、これはLiouville-von Neumann方程式と呼ばれます。Liouville-von Neumann方程式の解は、ハミルトニアンHが時間tを含まない場合にはρ = e^-i^H^tρ₀ eⁱ^H^tとなります。また、オブザーバブルωの期待値の時間変化d<ω>/dt = Tr{dρ/dt ω} = Tr{i(ρH-Hρ)ω} = Tr{i[ρ,H]ω}となります。

　z軸方向へかけられた静磁場B₀中（H = -ω₀Iz）における、全スピンが|ψ> = 1/2^1/2(|+> + |->)という状態の時間変化は

ρ₀		eⁱ^H^t		ρ		*ρIx*		*ρIy*		*ρIz*
1/2	1/2	e^-iω0t/2	0	1/2	1/2 e^iω0t	1/4 e^iω0t	1/4	-1/4i e^iω0t	1/4i	1/4	-1/4 e^iω0t
1/2	1/2	0	e^iω0t/2	1/2e^-iω0t	1/2	1/4	1/4 e^-iω0t	-1/4i	1/4i e^-iω0t	1/4e^-iω0t	-1/4

となるので、<Ix> = 1/2 cosω₀t、<Iy> = -1/2 sinω₀t、<Iz> = 0となり、磁化ベクトルがLarmor歳差運動をすることが分かります。また

ρ		H		[ρ,H]		i[ρ,H] Ix		i[ρ,H] Iy		i[ρ,H] Iz
1/2	1/2 e^iω0t	-1/2ω₀	0	0	1/2ω₀ e^iω0t	i/4ω₀ e^iω0t	0	-1/4ω₀ e^iω0t	0	0	-i/4ω₀ e^iω0t
1/2 e^-iω0t	1/2	0	1/2ω₀	-1/2ω₀ e^-iω0t	0	0	-i/4ω₀ e^-iω0t	0	-1/4ω₀ e^-iω0t	-i/4ω₀ e^-iω0t	0

となります。d<Ix>/dt = -1/2ω₀sinω₀t、d<Iy>/dt = -1/2 ω₀cosω₀t、d<Iz>/dt = 0となり上での結果に対応します。

回転座標系への変換

　ハミルトニアンH = H₀ + H₁と表せる場合でH₀があらわに時間tを含んでいない場合を考えます。Liouville-von Neumann方程式に対してρ = e^-i^H_⁰^tρ' e^iH₀tを代入すると、dρ'/dt = i(ρ'e^iH₀tH₁e^-i^H_⁰^t-e^iH₀tH₁e^-i^H_⁰^tρ') = i[ρ',e^iH₀tH₁e^-i^H_⁰^t]という式が導出できます。つまりρ→ρ' = eⁱ^H_⁰^tρ e^-iH₀t、H→H' = e^iH₀t(H - H₀)e^-iH₀tと置き換えを行なった場合もLiouville-von Neumann方程式はそのまま成立します。特にH₁ = 0ならばH' = 0なのでこの置き換えによりハミルトニアンの影響を完全に除去したことに相当します。

　ベクトルモデルにおいては、実験室座標系からLarmor周波数ω₀で回転する回転座標系に視点を変えることで静磁場B₀の影響を除去することが良く行われています。これを密度行列に対して行うのは上に述べた方法においてH₀ = -ω₀Izとした場合に相当しますから、ρ→ρ' = e^-iω0^Iz^tρ e^iω0^Iz^t、H→H' = e^-i^ω0Izt(H + ω₀Iz )e^iω0Iztと置き換えればよいのです。

　z軸方向へかけられた静磁場B₀中（H = -ω₀Iz）における、全スピンが|ψ> = 1/2^1/2(|+> + |->)という状態の時間変化は、この変換を行うと

ρ		H		e^iω0^Iz^t		ρ'		H'
1/2	1/2 e^iω0t	-1/2ω₀	0	e^iω0t/2	0	1/2	1/2	0	0
1/2 e^-iω0t	1/2	0	1/2ω₀	0	e^-iω0t/2	1/2	1/2	0	0

となります。これはρをt = 0で凍結したのと同じことになります。

　よって<Ix> = 1/2 cosω₀t 、<Iy> = -1/2 sinω₀t、<Iz> = 0をt = 0で凍結したのと同じことになり、磁化ベクトルは歳差運動せずx軸上に静止していることになります。このようにして静磁場の影響を考えなくてすむようにできます。

パルスの効果

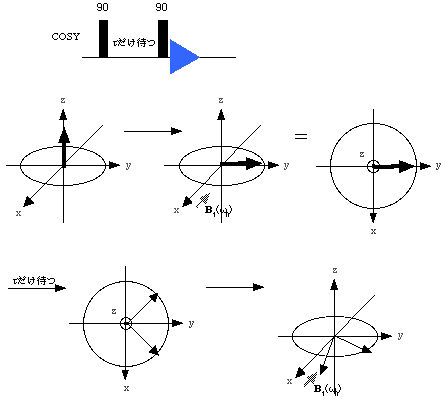
　ベクトルモデルにおいては、z軸方向を向いた磁化ベクトルが実験室座標系における周波数ω₀の回転磁場B₁（つまり回転系で見ると静磁場B₁）でxy平面に倒れることで、NMR信号が観測されるというモデルになっています。これを密度行列表示で表現すると次のようになります。

　まず、z軸方向へ静磁場B₀がかかっている系（H = -ω₀Iz）を考えます。この場合それぞれのスピンは|+>か|->のいずれかの状態を占めており、また|+>が占められている確率w₊= 1/Z e^{1/2kT(h/2π)ω0}、|->が占められている確率w_-= 1/Z e^{-1/2kT(h/2π)ω0}と、|+>の方が|->よりわずかに多い確率で占められています（Zは分配関数）。この場合の密度行列ρ₀は

ρ₀
w₊	0
0	w_-

　ここに、周波数ω₀の回転磁場B₁をかけます。するとハミルトニアンH = -ω₀Iz +γ B₁(Ixcosω₀t-Iysinω₀t)となります。これを行列で表示すると

H
-1/2ω₀	1/2γ B₁e^iω0t
1/2γ B₁e^-iω0t	1/2ω₀

　さてここからρの時間変化を追跡したいところですが、ハミルトニアンHの中にtがあらわに含まれているためLiouville-von Neumann方程式の解は単純にρ = e^-i^H^tρ₀ eⁱ^H^tとはなりません。そこでここで系を実験室座標系から回転座標系に変換します。ρ₀→ρ₀' = e^-iω0^Iz^tρ₀ e^iω0^Iz^t、H→H' = e^-iω0Izt(H + ω₀Iz )e^iω0Izt。すると

*ρ₀'*		H'
w₊	0	0	1/2γ B₁
0	w_-	1/2γ B₁	0

となりH'にはtが含まれません。よってρ'の時間変化は ρ' = e^-i^H'^tρ₀ 'eⁱ^H'^tで表すことができます。これを計算すると

eⁱ*^H'*^t		ρ'
cos(1/2γB₁t)	isin(1/2γB₁t)	1/2(w₊+w_-) + 1/2(w₊-w_-)cosγB₁t	1/2i(w₊ - w_-)sinγB₁t
isin(1/2γB₁t)	cos(1/2γB₁t)	-1/2i(w₊-w_-)sinγB₁t	1/2(w₊+w_-) - 1/2(w₊-w_-)cosγB₁t

ここから<Ix>、<Iy>、<Iz>を計算すると<Ix> = 0、<Iy> = -1/2(w₊-w_-)sinγB₁t、<Iz> = 1/2(w₊-w_-)cosγB₁tとなります。よってx軸方向からパルスを与えるとz軸上にあった磁化ベクトルはx軸の周りを γ B₁という（角）周波数で回転することが分かります。このようにしてパルスによって磁化ベクトルが倒れるという挙動も再現することができます。なお、γ B₁tをパルス幅といい、γ B₁t = π/2の時を90度パルス、γ B₁t = πの時を180度パルスといったりします。

直積演算子（プロダクトオペレーター）法

　さて、今まで長々と密度行列をあらわに扱って、それとベクトルモデルとの関係を見てきました。しかし、やはり行列を露わに扱って計算するのは面倒ですし分かりにくくもあります。そこで次のような取り扱いをします。

　まず、密度演算子ρ₀を4つの演算子E、Ix、Iy、Izの線形結合で表します。すなわちρ₀ = c_EE+c_xIx+c_yIy+c_zIzと表します。そして密度演算子ρ₀の時間変化を考えます。ρ = e^-i^H^tρ₀ eⁱ^H^tですからρ= c_Ee^-i^H^tEeⁱ^H^t+c_xe^-i^H^tIxeⁱ^H^t+c_ye^-i^H^tIyeⁱ^H^t+c_ze^-i^H^tIzeⁱ^H^t。よってe^-i^H^tAeⁱ^H^tというのを表にしておけばρの時間変化を簡単に求めることができます。例えば下の表からIyはH = ωIxの時にはIycosω t + Izsinω tと時間変化することが分かります。

A/H	ωE	ωIx	ωIy	ωIz
E	E	E	E	E
Ix	Ix	Ix	Ixcosωt - Izsinωt	Ixcosωt + Iysinωt
Iy	Iy	Iycosωt + Izsinωt	Iy	Iycosωt - Ixsinωt
Iz	Iz	Izcosωt - Iysinωt	Izcosωt + Ixsinωt	Iz

また、磁化ベクトルの期待値を計算する場合にもρ = c_EE+c_xIx+c_yIy+c_zIzと表しておくと、<Ix> = c_x、<Iy> = c_y、<Iy> = c_zとなりますから非常に都合が良くなります。このような手法を直積演算子法（プロダクトオペレーター法）といいます。

　みれば分かるようにEという部分はいかなるハミルトニアンの場合にもまったく変化せず、磁化ベクトルにも寄与しないことが分かります。すなわちこの部分は一切NMRに関与しない部分です。そのため普通省略されます。

　この手法は系を実験室座標系から回転座標系に移した場合の密度演算子とハミルトニアンの変換にも有効です。

スピンの相互作用

　いままではスピンと周囲の環境やスピン同士の相互作用を扱ってきませんでした。しかしNMRではこれらが化学シフト、スピン－スピンカップリングといった形でスペクトルに現れ、重要な情報となります。

化学シフト

　スピンの周囲の環境によって、スピンが存在する位置での実効的な静磁場がB₀からB₀(1-Σ)となったとすれば、そのスピンに対するハミルトニアンH = -γB₀(1-Σ)Iz = -ωIzとなります。このように周囲の環境によってLarmor周波数が変化しますが、その量を化学シフトといいます。実験室座標系でハミルトニアンH = -ωIzの場合に、この系を周波数ω₀で回転する座標系に移すとH→H '= ω₀Iz + e^-iω0^Iz^tH e^iω0^Iz^t= (ω₀-ω)Izとなります。

　z軸方向へ静磁場がかかっている系の密度演算子ρ'= 1/2(w₊ + w_-)E + (w₊ - w_-)Izは、90度xパルスによってρ'= 1/2(w₊ + w_-)E - (w₊ - w_-)Iyに変化します。ここでパルスを止めてやるとH '= (ω₀-ω)Izならばρ'= 1/2(w₊ + w_-)E - (w₊ - w_-){Iycos(ω₀-ω) t - Ixsin(ω₀-ω) t}となって磁化ベクトルはy軸上で静止せず、xy平面内を周波数ω₀-ωで回転することになります。これは磁化ベクトルにおける化学シフトの描写とも一致しています。

　なお実際には静磁場B₀は周囲の環境によってB₀(1-Σ)のように単純にスカラー倍されるわけではなく、x軸方向やy軸方向への成分を持つことになります。すなわちベクトルB₀に対して行列(E-Σ)が作用して新しいベクトルになるという描写になります。この行列(E-Σ)は化学シフトテンソルと呼ばれます。磁場がx軸方向やy軸方向を持つということはこの方向にもスピンが歳差運動するということになり、スピンのx軸、y軸成分も化学シフトに影響してきます。しかし、液体中のようにスピンが所属している分子が十分に速く熱運動している場合にはこれらの影響は全て相殺されてしまい、結局B₀(1-Σ)のようにスカラー倍して考えた場合と同じ結果が得られるためにこのような取り扱いをするわけです。固体のNMRでは分子の熱運動が束縛されているために、単純にスカラー倍で考えることはできません。

スピン－スピンカップリング

　スピンが2つ存在すると、その配向が平行か、反平行かによってLarmor周波数に変化が起こります。これをスピン－スピンカップリングといいます。2つのスピンをI、Sとすれば、ハミルトニアンH = 2πJIS = 2πJ(IxSx + IySy + IzSz)と表記できます。そして、さらにI、SのLarmor周波数の差Δω>>2πJの場合(スペクトルがいわゆるAXパターンになる程度に化学シフトが離れている場合）にはIxSx + IySyの部分は無視できてH = 2πJ IzSzと表記できます。まだ2つのスピンを同時に扱う密度演算子を出していませんので、これによって密度演算子ρがどのように時間変化するかは後述します。

2スピン系への密度演算子の拡張

　いままで扱ってきたのは相互作用のない（＝孤立した）スピン系の密度演算子でした。しかし、実際にはスピンはお互いに相互作用を及ぼしあっており、独立に取り扱えるわけではありません。ここでは相互作用している2つのスピンを密度演算子でどのように記述するのかを述べます。

　まず、2つのスピンIおよびSを考えます。すると、これにはそれぞれ|+>、|->の状態があるので、2スピン系には|++>、|+->、|-+>、|-->という4つの状態があるということになります（前側の符号がIに、後側の符号がSに対応するとします）。演算子については

Iz|+S> = 1/2|+S>、Iz|-S> = -1/2|-S>
I²|+S> = 1/2(1+1/2)|+S>、I²|-S> = 1/2(1+1/2)|-S>
I₊|+S> = 0、I₊|-S> = |+S>
I_-|+S> = |-S>、I_-|-S> = 0
E|+S> = |+S>、E|-S> = |-S>

のようにIに対する演算子はSの部分に対しては何の作用もしないとします（逆にSに対する演算子はIの部分に対しては何の作用もしない。)このようにすると次のようにスピンの状態は4列のベクトルで表すことができます。

\|++>	\|+->	\|-+>	\|-->
1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

また各演算子は4×4の行列で表すことができます。

E				Ix				Iy				Iz				I₊				*I_-*
1	0	0	0	0	0	1/2	0	0	0	1/2i	0	1/2	0	0	0	0	0	1	0	0	0	0	0
0	1	0	0	0	0	0	1/2	0	0	0	1/2i	0	1/2	0	0	0	0	0	1	0	0	0	0
0	0	1	0	1/2	0	0	0	-1/2i	0	0	0	0	0	-1/2	0	0	0	0	0	1	0	0	0
0	0	0	1	0	1/2	0	0	0	-1/2i	0	0	0	0	0	-1/2	0	0	0	0	0	1	0	0
				Sx				Sy				Sz				S₊				*S_-*
				0	1/2	0	0	0	1/2i	0	0	1/2	0	0	0	0	1	0	0	0	0	0	0
				1/2	0	0	0	-1/2i	0	0	0	0	-1/2	0	0	0	0	0	0	1	0	0	0
				0	0	0	1/2	0	0	0	1/2i	0	0	1/2	0	0	0	0	1	0	0	0	0
				0	0	1/2	0	0	0	-1/2i	0	0	0	0	-1/2	0	0	0	0	0	0	1	0

ρ
Σw_ic_i++c_i++^*	Σw_i c_i++c_i+-^*	Σw_ic_i++c_i-+^*	Σw_i c_i++c_i--^*
Σw_ic_i+-c_i++^*	Σw_i c_i+-c_i+-^*	Σw_ic_i+-c_i-+^*	Σw_i c_i+-c_i--^*
Σw_ic_i-+c_i++^*	Σw_i c_i-+c_i+-^*	Σw_ic_i-+c_i-+^*	Σw_i c_i-+c_i--^*
Σw_ic_i--c_i++^*	Σw_i c_i--c_i+-^*	Σw_ic_i--c_i-+^*	Σw_i c_i--c_i--^*

です。というわけで2スピン系での行列表示は極めて煩雑になります。なので一般に直積演算子法による取り扱いが行われるわけです。

　直積演算子法を使用する場合1スピン系では密度演算子ρを4つの演算子E、Ix、Iy、Izの和で表しましたが、2スピン系では16個の演算子が必要になります。これは1つのスピンだけに関わるIx、Iy、Iz、Sx、Sy、Szに加えて2スピンに同時に作用する2IxSx、2IxSy、2IxSz、2IySx、2IySy、2IySz、2IzSx、2IzSy、2IzSz、そしてNMRには関与しない部分Eの16個です。なお、これらを外積の形で表記すると

Ix = 1/2 (|++><-+| + |+-><--| +|-+><++| + |--><+-| )
Iy = 1/2i (|++><-+| + |+-><--| -|-+><++| - |--><+-| )
Iz = 1/2 (|++><++| + |+-><+-| - |-+><-+| - |--><--| )
Sx = 1/2 (|++><+-| + |+-><++| +|-+><--| + |--><-+| )
Sy = 1/2i (|++><+-| - |+-><++| +|-+><--| - |--><-+| )
Sz = 1/2 (|++><++| - |+-><+-| + |-+><-+| - |--><--| )
2IxSx = 1/2(|++><--| + |+-><-+| + |-+><+-| +|--><++|)
2IxSy = 1/2i(|++><--| - |+-><-+| + |-+><+-| -|--><++|)
2IxSz = 1/2(|++><-+| - |+-><--| + |-+><++| -|--><+-|)
2IySx = 1/2i(|++><--| + |+-><-+| - |-+><+-| -|--><++|)
2IySy = 1/2(-|++><--| + |+-><-+| + |-+><+-| -|--><++|)
2IySz = 1/2i(|++><-+| - |+-><--| - |-+><++| +|--><+-|)
2IzSx = 1/2(|++><+-| + |+-><++| - |-+><--| -|--><-+|)
2IzSy = 1/2i(|++><+-| - |+-><++| - |-+><--| +|--><-+|)
2IzSz = 1/2(|++><++| - |+-><+-| - |-+><-+| +|--><--|)
E = |++><++| + |+-><+-| + |-+><-+| +|--><--|

となります。

　これら2スピン系の行列表示は1スピンだけの時の演算子の行列表示の直積になります(これが直積演算子法と呼ばれる所以)。行列A、Bに対する直積A⊗Bは次のように定義されます。なお、2スピン系でのIxはIx(1スピン系)⊗E(1スピン系)、SxはE(1スピン系)⊗Sx(1スピン系)になっています（直積はA⊗B≠B⊗Aですから別の表現になります）。

A⊗B

Ix(1スピン系)

Sz(1スピン系)

IxSz(2スピン系)
= Ix(1スピン系)⊗Sz(1スピン系)

1/2

1/4

-1/4

1/2

-1/2

1/4

-1/4

　次にこれらの演算子がどのように時間変化するかを調べます。しかし、基本的にはIに対する演算子はSの部分に対しては何の作用もしない（逆もそう）ので、IとSは独立して取り扱いができます。つまりIzSzという演算子がH = ω_IIx + ω_SSyというハミルトニアンで時間変化する場合、(Izcosω_It - Iysinω_It)(Szcosω_St +Sxsinω_St)になるとしてよいわけです。

A/H	ωE	ωIx	ωIy	ωIz
E	E	E	E	E
Ix	Ix	Ix	Ixcosωt - Izsinωt	Ixcosωt + Iysinωt
Iy	Iy	Iycosωt + Izsinωt	Iy	Iycosωt -Ixsinωt
Iz	Iz	Izcosωt - Iysinωt	Izcosωt +Ixsinωt	Iz

　また、2スピン系ではスピン－スピンカップリングが存在し、このハミルトニアンは(Δω>>2πJの場合)H = 2πJIzSzと表せます。この場合の時間変化は

A/H	2πJIzSz
Ix	IxcosπJt + 2IySzsinπJt
Iy	IycosπJt - 2IxSzsinπJt
2IxSz	2IxSzcosπJt + IysinπJt
2IySz	2IySzcosπJt - IxsinπJt
Sx	SxcosπJt + 2IzSysinπJt
Sy	SycosπJt - 2IzSxsinπJt
2IzSx	2IzSxcosπJt + SysinπJt
2IzSy	2IzSycosπJt - SxsinπJt
そのほか	変化しない

となります。

　磁化ベクトルの期待値を計算する場合には寄与するのは<Ix> にはIx、<Iy> には Iy、<Iz> にはIz、<Sx> にはSx、<Sy> には Sy、<Sz> にはSzだけです。そのほかの演算子は磁化ベクトルに対して何の寄与もしません。つまりこれらの項はベクトルモデルによっては表現できない（一部にできるものもありますが）のです。これがCOSYのようなスペクトルをベクトルモデルで記述できない理由になっています。

二重回転座標系

　スピンIとSが異なる種類の核である場合（例えば¹Hと¹³Cとか）、そのLarmor周波数は大きく異なっています。この場合には、スピンIはIのLarmor周波数ω_I0で、スピンSはSのLarmor周波数ω_S0で回転する回転座標系から観測するのが好都合です。二重回転座標系への変換は回転座標系のへの変換のところで述べた変換をそれぞれのLarmor周波数に対して行なうことによってなされます。すなわちρ₀→ρ₀' = e^-iωS0^Sz^te^-iωI0^Iz^tρ₀ e^iωI0^Iz^te^iωS0^Sz^t、H→H' = e^-iωS0^Sz^te^-iωI0^Iz^t(H + ω_I0Iz + ω_S0Sz)e^iωI0^Iz^te^iωS0^Sz^tという変換によってなされます。Iに対する演算子はSの部分に対しては何の作用もしない（逆もそう）ので、それぞれ独立にIとSを回転座標系に移せばよいことになります。

　では、実際に直積演算子法で2スピン系のスペクトルを再現してみます（二重回転座標系で扱います）。

　まず最初の密度演算子はρ₀ = Iz + Szと表せます（NMRに関与しない演算子Eおよび Iz 、Szに掛かっている係数を省略しています）。

　ここに両方のスピンに90度xパルスを当てます。このハミルトニアンはH = γB₁(Ix + Sx)と表せます。すると、 Iz → IzcosγB₁ t - IysinγB₁ tのγB₁ t = 90度のときですからρ₁ = -Iy - Syとなります。

　このあと、それぞれの演算子は化学シフトとスピン－スピンカップリングによって時間変化します。ハミルトニアンはH = (ω_I0-ω_I)Iz + (ω_S0-ω_S)Sz+ 2πJIzSzです。

　まず(ω_I0-ω_I)Iz による時間変化を考えるとIy→Iycosω t -Ixsinω tですから、ρ₂= -( Iycos (ω_I0-ω_I) t -Ixsin (ω_I0-ω_I) t)-Syとなります。

　次に(ω_S0-ω_S)Sz による時間変化を考えるとSy→Sycosω t -Sxsinω tですから、ρ₃= -( Iycos (ω_I0-ω_I) t -Ixsin (ω_I0-ω_I) t)-( Sycos (ω_S0-ω_S) t -Ixsin (ω_S0-ω_S) t)となります。

　さらに 2πJIzSzによる時間変化を考えるとρ₄= -( (Iycos πJt - 2IxSzsin πJt)cos (ω_I0-ω_I) t -(Ixcos πJt + 2IySzsin πJt)sin (ω_I0-ω_I) t)-( (Sycos πJt - 2IzSxsin πJt)cos (ω_S0-ω_S) t -(Sxcos πJt + 2IzSysin πJt)sin (ω_S0-ω_S) t)です。さてこの中で磁化ベクトルに関係のある演算子部分だけを抜き出すと-Iycos πJt cos (ω_I0-ω_I) t +Ixcos πJt sin (ω_I0-ω_I) t- Sycos πJt cos (ω_S0-ω_S) t +Sxcos πJt sin (ω_S0-ω_S) tです。よって

<Ix> = cos πJt sin (ω_I0-ω_I) t = 1/2(sin (ω_I0-ω_I+πJ)t + sin (ω_I0-ω_I-πJ)t)
<Iy> = -cos πJt cos (ω_I0-ω_I) t = -1/2(cos (ω_I0-ω_I+πJ)t + cos (ω_I0-ω_I-πJ)t)
<Sx> =cos πJt sin (ω_S0-ω_S) t = 1/2(sin (ω_S0-ω_S+πJ)t + sin (ω_S0-ω_S-πJ)t)
<Sy> =- cos πJt cos (ω_S0-ω_S) t = -1/2(cos (ω_S0-ω_S+πJ)t + cos (ω_S0-ω_S-πJ)t)

となります。観測される磁化ベクトル<Iy>は (ω_I0-ω_I+πJ)、 (ω_I0-ω_I-πJ)という周波数で運動していますから、これをフーリエ変換すれば、Iに対応する (ω_I0-ω_I+πJ)、 (ω_I0-ω_I-πJ)というダブレットがスペクトルに現れます。また同様にして<Sy>からはSに対応する (ω_S0-ω_S+πJ)、 (ω_S0-ω_S-πJ)というダブレットがスペクトルに現れることが分かります。

　この今まで行ってきた結論を次のように系統樹で書くことがあります。これの見方は例えばIzは90度xパルスで-Iyに変化し、これはさらにハミルトニアンの化学シフト(ω_I0-ω_I) Izによって-Iycos(ω_I0-ω_I ) tとIxsin(ω_I0-ω_I ) tになることを示しています（つまり上段がcos項、下段がsin項です。2段に分かれないところは時間変化しないか、ただ1つの項しか出てこない場合です）。逆にSxという項はSzからたどると、化学シフトIでは変化せず（係数なし）、化学シフトSではsin項として（係数sin(ω_S0-ω_S) がついて）、カップリングではcos項として（係数cos πJtがついて）生成していることから最後にはSxsin(ω_S0-ω_S) cos πJtという形になっていることが読みとれるわけです。

90度xパルス	化学シフトI	化学シフトS	カップリング
Iz →-Iy	*-Iy*	*-Iy*	*-Iy*
			2IxSz
	Ix	Ix	Ix
			2IySz
Sz→*-Sy*	*-Sy*	*-Sy*	*-Sy*
			2IzSx
		Sx	Sx
			2IzSy

2次元NMR

　磁化ベクトル<Iy> = cosω₁t₁cosω₂t₂と表せる場合を考えてみます。これをt₁を定数、t₂を変数と見て、フーリエ変換します（t₂についてのフーリエ変換）。するとこれは周波数ω₂の位置にcosω₁ t₁という大きさのピークがあるスペクトルが得られます。つまりt₁の値によってピークの大きさが変わるわけです。今度はt₁を変数と見ます。t₁に対してピークの大きさcosω₁t₁をプロットしたものをインターフェログラムといいます。このインターフェログラムcosω₁t₁をもう一回フーリエ変換してやります（t₁についてのフーリエ変換）。すると、こちらでは周波数ω₁の位置にピークが現れます。ここで横軸に最初のフーリエ変換で現れる周波数、縦軸に2回目のフーリエ変換で現れる周波数をとった2次元のチャートをつくり、（ω₂，ω₁）にピークが出るものとします。これが2次元NMRのチャートです。

　磁化ベクトルが複数の周波数成分を持っていて、例えば<Iy> = cosω₁t₁cosω₂t₂+ cosω₃t₁cosω₄t₂と表せるときを考えます。t₂についてのフーリエ変換でまずω₂において cosω₁t₁、ω₄において cosω₃t₁という大きさのピークが現れるスペクトルが得られます。そしてここからそれぞれω₂、ω₄についてインターフェログラムを考えます。まず、ω₂のインターフェログラムをt₁についてフーリエ変換するとω₁にピークが現れます。次にω₄のインターフェログラムに対してはω₃にピークが現れます。これを2次元チャートにすると（ω₂，ω₁）および（ω₄，ω₃）にピークが現れます。

　つまり2次元NMRはt₁を変化させながら何度も測定を行い、それぞれの測定によって得られるチャートのt₁によるピークの大きさの変化をもう一つの軸に投影するわけです。例えばCOSYならばピークの大きさがカップリング相手の共鳴周波数で変動するためにカップリング相手が分かるのです。

COSYを直積演算子法で記述する

　さて、これで最初に挙げた疑問を解決することができます。COSYのパルスシーケンスは最初に挙げたとおり

まず90度xパルスを当て、
t₁だけ待ち
再び90度xパルスを当て、
その直後から磁化ベクトルを観測する

というものです。それに従って密度演算子の時間変化を追跡していきます。

　まず最初の密度演算子は静磁場中に置かれているスピンのものですから、ρ₀ = Iz + Szと表せます（NMRに関与しない演算子Eおよび Iz 、Szに掛かっている係数を省略しています）。

　ここに両方のスピンに第1の90度xパルスを当てます。このハミルトニアンはH = γB₁(Ix + Sx)と表せます。すると、 ρ₁ = -Iy - Syとなります。

　このあとt₁の間だけ、それぞれの演算子は化学シフトとスピン－スピンカップリングによって時間変化します。ハミルトニアンはH = (ω₀-ω_I)Iz + (ω₀-ω_S)Sz+ 2πJIzSzです。

　まず化学シフトの部分による時間変化を考えるとρ₂= -( Iycos (ω₀-ω_I) t₁ -Ixsin (ω₀-ω_I) t₁)-( Sycos (ω₀-ω_S) t₁ -Ixsin (ω₀-ω_S) t₁)となります。

　ここにさらにスピン－スピンカップリングの部分による時間変化を考えるとρ₃= -( (Iycos πJ t₁ - 2IxSzsin πJ t₁)cos (ω₀-ω_I) t₁ -(Ixcos πJ t₁ + 2IySzsin πJ t₁)sin (ω₀-ω_I) t₁)-( (Sycos πJ t₁ - 2IzSxsin πJ t₁)cos (ω₀-ω_S) t -(Sxcos πJ t₁ + 2IzSysin πJ t₁)sin (ω₀-ω_S) t₁)です。(ここまでは前に述べた2スピン系の密度演算子の時間変化と同じです。）

　ここに両方のスピンに第2の90度xパルスを当てます。このハミルトニアンは第1の90度xパルスと同じくH = γB₁(Ix + Sx)と表せます。よってρ₄= -( (Izcos πJ t₁ + 2IxSysin πJ t₁)cos (ω₀-ω_I) t₁ -(Ixcos πJ t₁ - 2IzSysin πJ t₁)sin (ω₀-ω_I) t₁)-( (Szcos πJ t₁ + 2IySxsin πJ t₁)cos (ω₀-ω_S) t -(Sxcos πJ t₁ - 2IySzsin πJ t₁)sin (ω₀-ω_S) t₁)です。

　このあとそれぞれの演算子は化学シフトとスピン－スピンカップリングによって時間変化します。これを検出することになるわけです。時間をt₂で表します。しかし、このまま密度演算子を追跡していくのは項の数が激増して困難です。よって最終的に検出される磁化ベクトルに対応する演算子であるIy、Syが時間変化によってどの項から導かれるかを前もって考えます。まずスピン－スピンカップリングによってIy、Syが導かれるのは、Iy、Sy、IxSz、IzSxの4つの演算子からです。次に化学シフトによってこの4つの演算子が導かれるのは、Ix、Iy、Sx、Sy、IxSz、IySz、IzSx、IzSyの８つの演算子からです。よってこれらの演算子を含む項を抜き出すとρ₄' = (Ixcos πJ t₁ - 2IzSysin πJ t₁)sin (ω₀-ω_I) t₁+(Sxcos πJ t₁ - 2IySzsin πJ t₁)sin (ω₀-ω_S) t₁。

　これに対して化学シフトの部分による時間変化を考えるとρ₅ = ((Ixcos(ω₀-ω_I) t₂ + Iysin(ω₀-ω_I) t₂)cos πJ t₁ - 2Iz(Sycos (ω₀-ω_S) t₂ -Sxsin (ω₀-ω_S) t₂ )sin πJ t₁)sin (ω₀-ω_I) t₁+((Sxcos(ω₀-ω_S) t₂ + Sysin(ω₀-ω_S) t₂)cos πJ t₁ - 2(Iycos (ω₀-ω_I) t₂ -Ixsin (ω₀-ω_I) t₂ )Szsin πJ t₁)sin (ω₀-ω_S) t₁。スピン－スピンカップリングによってIy、Syが導かれるのは、Iy、Sy、IxSz、IzSxの4つの演算子からですので、それらの項だけを抜き出してρ₅' = (Iysin(ω₀-ω_I) t₂cos πJ t₁ + 2IzSxsin (ω₀-ω_S) t₂ sin πJ t₁)sin (ω₀-ω_I) t₁+(Sysin(ω₀-ω_S) t₂cos πJ t₁ + 2IxSzsin (ω₀-ω_I) t₂ sin πJ t₁)sin (ω₀-ω_S) t₁。

　さらにスピン－スピンカップリングの部分による時間変化を考えるとρ₆ = ((Iycos πJt₂ - 2IxSzsin πJt₂ )sin(ω₀-ω_I) t₂cos πJ t₁ + (2IzSxcos πJt₂ + Sysin πJt₂ )sin (ω₀-ω_S) t₂ sin πJ t₁)sin (ω₀-ω_I) t₁+((Sycos πJt₂ - 2IzSxsin πJt₂ )sin(ω₀-ω_S) t₂cos πJ t₁ + (2IxSzcos πJt₂ + Iysin πJt₂ )sin (ω₀-ω_I) t₂ sin πJ t₁)sin (ω₀-ω_S) t₁

　よって

<Iy> = cos πJt₂sin(ω₀-ω_I) t₂cos πJ t₁sin (ω₀-ω_I) t₁+ sin πJt₂ sin (ω₀-ω_I) t₂ sin πJ t₁sin (ω₀-ω_S) t₁= 1/4{sin(ω₀-ω_I + πJ ) t₂ + sin(ω₀-ω_I - πJ ) t₂}{sin (ω₀-ω_I +πJ ) t₁+sin (ω₀-ω_I -πJ ) t₁}
+ 1/4{cos(ω₀-ω_I - πJ ) t₂ - cos(ω₀-ω_I + πJ ) t₂}{cos(ω₀-ω_S - πJ ) t₁ - cos(ω₀-ω_S + πJ ) t₁}
<Sy> = sin πJt₂ sin (ω₀-ω_S) t₂ sin πJ t₁sin (ω₀-ω_I) t₁+cos πJt₂ sin(ω₀-ω_S) t₂cos πJ t₁ sin (ω₀-ω_S) t₁= 1/4{cos(ω₀-ω_S - πJ ) t₂ - cos(ω₀-ω_S + πJ ) t₂}{cos(ω₀-ω_I - πJ ) t₁ - cos(ω₀-ω_I + πJ ) t₂}
+ 1/4{sin(ω₀-ω_S + πJ ) t₂ + sin(ω₀-ω_I - πJ ) t₂}{sin(ω₀-ω_S + πJ ) t₁ + sin(ω₀-ω_S - πJ ) t₁}

となります。<Iy> では t₁軸でω₀-ω_I ±πJ、 t₂軸でω₀-ω_I ± πJの位置の対角ピークと、 t₁軸でω₀-ω_S ±πJ、 t₂軸でω₀-ω_I ± πJの位置の交差ピークが、<Sy>では t₁軸でω₀-ω_S ±πJ、 t₂軸でω₀-ω_S ± πJの位置の対角ピークと、 t₁軸でω₀-ω_I ±πJ、 t₂軸でω₀-ω_S ± πJの位置の交差ピークが検出されるということが分かります。

　ここまで露わに計算してきましたが、系統樹に書き換えると次のようになります（Izの方だけ)。

90度xパルス	化学シフトI	カップリング、90度xパルス	化学シフトI	化学シフトS	カップリング
Iz→-Iy	*-Iy*	*-Iy*→-Iz	-Iz	-Iz	-Iz



		2IxSz→-2IxSy	-2IxSy	-2IxSy	-2IxSy
				2IxSx	2IxSx
			-2IySy	-2IySy	-2IySy
				2IySx	2IySx
	Ix	Ix	Ix	Ix	Ix
					2IySz
			Iy	Iy	Iy : 対角ピーク
					- 2IxSz
		2IySz→-2IzSy	-2IzSy	-2IzSy	-2IzSy
					Sx
				2IzSx	2IzSx
					Sy : 交差ピーク

　この表を見ると対角ピークはIz→-Iy→Ix→IyとIのスピン演算子のみを経由して得られているのに対し、交差ピークはIz→-Iy→Ix→2IySz→-2IzSy→2IzSx→SyとIのスピン演算子からSのスピン演算子に変化していったことが分かります。つまり最初<Iz>だった磁化が最後には<Sy>として観測されたということになります。このようにあるスピンの磁化を別のスピンの磁化として観測することをコヒーレンス移動といいます。これは他にDEPTなどでも使用される方法です。

続く？