ヘルムホルツの分解定理について

＜はじめに＞

ヘルムホルツの分解定理とは、Wikiの 「ヘルムホルツの（分解）定理」 に示されている通り、ベクトル場を示す関数F（ｘ、ｙ、ｚ）が渦の無い ベクトルF_L（ｘ、ｙ、ｚ）と発散の無いベクトルF_T（ｘ、ｙ、ｚ）に分解で きると言う定理です。

流体力学では、流れの場をこのベクトルFと考え、任意の流れが渦の無い流れF_Lと発散の無い流れ F_Tに分解できると考えられています。

しかし、実際の任意の流れの場Fは渦無し流れと発散無し流れに分解できません。ちょっとした勘違いでこの定理は100年 以上も正しいと信じられ、いったん「定理」の名前をもらうと、なかなかこの「定理」に逆らうことは容易ではありません。

しかし、数学的な考察と、実際にこの定理を用いて、流れの場を分解したと言う結果を調べると、この「ヘルムホルツ の分解定理＝流れの場の分解定理」は間違っていることが分かります。

この定理を信じている流体力学の学者の中に2通りの人がいます。 一つのグループは、分解定理の定義からして、分解された流れの成分F_LとF_Tが 直交していると信じている人たちであり、この人たちは現実の流れを分解したことが無く、実際に分解してみると、分解 されたとする二つの流れの成分F_LとF_Tは直交していないことを知らない理論家 の人たちです。

もう一つのグループは現実の流れの分解を身近に実行している人たちです。たとえば、気象庁の予報の関係者などは毎日 実際の風（流れ）成分を「分解して」居ますので、2成分が直交していないのを日夜見て、経験的に知っています。 第2のグループの人たちも、初めにヘルムホルツの分解定理を学生として学んだ当時は、たぶん2成分が直交していると信 じていた筈ですが、実際の流れの場を分解して、現実には直交していないのを見ると、勝手な理屈を考えて、その“正当性” を作り上げて来た人たちです。

ベクトルの基本的な考えを無視しています。直交して居なければ他の成分を持っていると言うことに、目をつぶって「定理」を信じたいのです。

あなたは、あるいはあなたの先生は、どちらのグループに属していますか。

１：直交していないと何故いけないか

元の流れFから発散成分を取り出すには、∇・Fで求めることができ、渦成分を取り出すには∇×Fで取り出す ことができます。もしも、ヘルムホルツの分解定理が正しいなら下図に示すようにFが渦のみの成分と発散のみの成分に きれいに分解できるはずです。∇・Fの計算に用いられるFの成分はF_Lのみであ り、∇×Fの計算に用いられるFの成分はF_Tのみであるはずです。

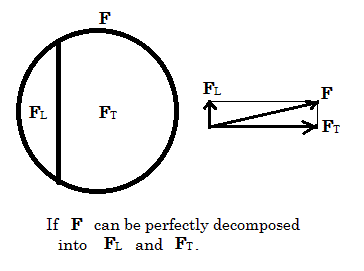
その場合は、F_L成分は渦成分を持たず、F_T成分は発散成分を持ちません。2つのベクトル が互いに他の成分を持っていない場合、ベクトルの性質からして、互いに直交しているはずです。このことは、次のように、直交 していない場合を考えるとより理解が深まります。

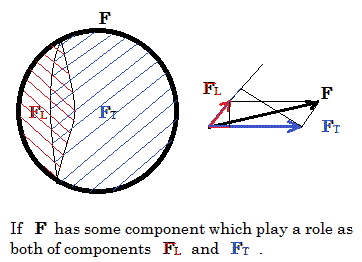
もしも流れの成分が、渦だけの成分と発散だけの成分のほか、両方に寄与する成分（分離できない成分）の3つの成分からできあ がっていたとしても、発散分布は∇・Fから、渦分布は∇×Fから求めることができます。

そして、この発散分布が渦なし流れと勘違いさえすれば、F_Lは求めることができますし、渦分布が発散無し 流れと勘違いさえすればF_Tを求めることができます。

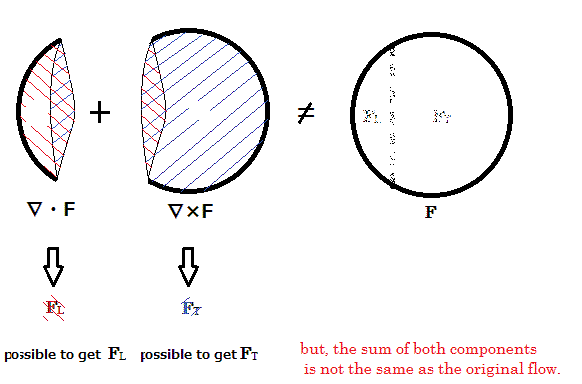
しかし、上の模式図を見れば明らかなように、これらの合成は元の流れとは違っています。この場合の合成されたベクトルを Dとすると、元の流れFとは違ったものになっています。すなわちD≠Fです。

もしも、両方に寄与する（どちらかに分解できない）成分があるのに、このような勘違をして得られている二つの流れ成分は、 渦だけの流れや発散だけの成分では無いため、互いに他の成分を持ち、上の模式図に示されるように直交していません。

逆に、実際の分解をやったとして得られているF_LとF_Tが直交して居ない場合は、 F_L＋F_T＝Dであって、元の流れを2つに分解できたことにはなっていません。つまり、 F_L＋F_T≠Fであったことを示しています。つまり渦と発散の両方に寄与する成分が 分解できなかったことを示しています。

このことは、分解の方法がまずかったか、あるいはヘルムホルツの分解定理が間違っているかのどちらかです。 ヘルムホルツの分解定理が正しいと判断するためには、この両方に寄与する成分が無いことを証明する必要があります。 あるいは実際の分解をやってみて、必ず分解した流れF_LとF_Tとが直交して居ること を示す必要があります。

２：実際の分解結果は？

次に、実際に「ヘルムホルツの分解定理」を用いて分解している？現状を見てみましょう

流れの中に渦が無ければ、速度ポテンシャルというスカラー関数が存在し、そのポテンシャルの傾きで、渦の無い発散流れが 求められます。また、流れの中に発散が無ければ、ベクトルポテンシャルAが存在し、その回転（∇×A）で発散の無い渦流れ が求められます。

気象庁では、ヘルムホルツの分解定理が正しいとして、毎日風の場を発散だけの風の場と、渦だけの風の場に分解し、それぞれ 「速度ポテンシャル」と「流線関数」として公表しています。

例えば2010年8月20日の日本時刻9時の２００ｈPa 天気図を雲（水蒸気）画像に重ねて下図の示します。

この図に示された黒い矢印は、実際に吹いていると解析された風で、矢の向きが風のベクトルの方向を、矢の長さが風速を示しています。

次にこの雲画像に、その実際の風をヘルムホルツの分解定理で分解して得られる「速度ポテンシャル」と「流線関数」から得られる それぞれ、発散風と渦風を赤い矢印と青い矢印で示します。

これらの二つの成分を同じ図に表示します。発散風を赤い矢印で、渦風を青い矢印では示します。多くの地点でこれら二つの成分は、直交して居ないことが確認できます。

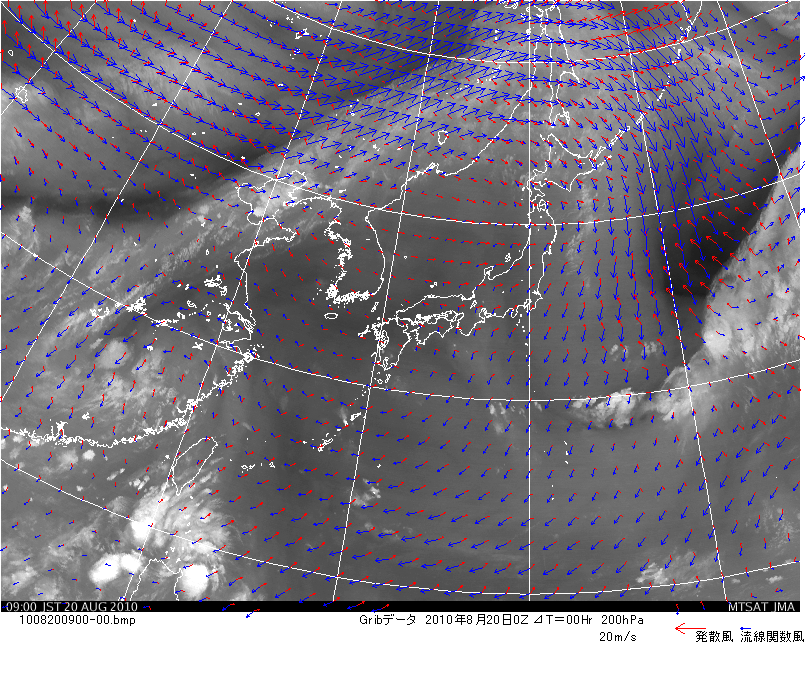
任意の流れである風の場をヘルムホルツの分解定理なるものを用いて分解したところ、理論的には直交 してあるべきものが直交して居ないと言う事実を示した図になっています。

気象庁の分解の方法がまずいのでしょうか。私はこれは、一般的に流れの場を発散だけの流れと渦だけの流れに分解できるとする「ヘルムホルツの分解定理」が間違っている証拠だと思います。 すなわち、一般に任意の流れには渦と発散の両方に寄与する成分が含まれていて、この成分を分解できないと考えます。

任意の流れが渦と発散だけに分解できないことは、非常に簡単に、ヘルムホルツの分解定理よりも基本的な、数学的な２つの定理 により証明することができます。

３：流れの分類

流れの特性を現す物理量に「渦の分布」と「発散の分布」があり、これらの有無によって、流れの場を分類することが出来ま す。

＜３−１＞　渦のない流れ

　渦のない流れについて、２次元で考えて見ます。横方向の座標をｘ、縦方向の座標をｙとし、横方向の流速をｕ、縦方向の流速 をｖで表しますと、
　渦度は∂ｖ／∂ｘ−∂u／∂ｙで現されますので、渦のない流れは、
∂ｖ／∂ｘ−∂u／∂ｙ＝０　　　・・・・・・・・・・・・１）
となっています。

　この１）式は、ある関数が存在し、その全微分がｕｄｘ＋ｖｄｙ　であるための必要十分条件です。その関数をχとする と、
ｄχ＝ｕｄｘ＋ｖｄｙ　　　・・・・・・・・・・・・・・・・・・・２）
と書くことが出来ます。

　一般に全微分とは考えられる方向の全ての方向の偏微分にその方向の微少変化量をかけたモノの総和で表されますから
ｄχ＝∂χ／∂ｘ・ｄｘ＋∂χ／∂ｙ・ｄｙ・・・・・・・・３）
　です。

従って、２）と３）から、渦のない流れの成分は関数χを用いて
ｕ＝∂χ／∂ｘ、
ｖ＝∂χ／∂ｙ
と表すことが出来ます。

　渦のない流れについては、スカラー関数χが存在し、その微分で流れの場を現すことができます。
　流体の中に渦が無いことは、その流れに速度ポテンシャルが存在するための必要十分条件となっています。

従って、流れに渦が有る場合には、その関数の傾きが流れの速度を現すようなスカラー関数 は存在しないことになります。

＜参考>「流体力学」岩本順二郎著、東京電機大学出版局

＜３−２＞　発散の無い流れ

　発散のない流れでは、ｕ，ｖをそれぞれ直交するｘ軸方向とｙ軸方向の流れの速度とすると発散量は、∂ｕ／∂ｘ＋∂ｖ／∂ｙ で現されますから、発散量の無い流れは
∂ｕ／∂ｘ＋∂ｖ／∂ｙ＝０　　　　・・・・・・・・・４）
となります。この式は書き直すと、
∂ｕ／∂ｘ−∂（−ｖ）／∂ｙ＝０・・・・・・・・・・５）
と書くことができます。

　この５）式は、ある関数が存在し、その全微分が（−ｖ）・ｄｘ＋ｕｄｙ　であるための必要十分条件です。その関数をαとする と、
ｄα＝（−ｖ）・ｄｘ＋ｕｄｙ　・・・・・・・・・・・・・・・・６）
と書くことが出来ます。

　一般に全微分とは考えられる方向の全ての方向の偏微分にその方向の微少変化量をかけたモノの総和で表されますから、今の 場合、２次元（ｘ、ｙ）で考えますと、
ｄα＝∂α／∂ｘ・ｄｘ＋∂α／∂ｙ・ｄｙ　・・・・・・・・・・７）
となります。

６）及び７）より、発散のない流れの各座標成分は関数αを用いて
−ｖ＝∂α／∂ｘ
ｕ＝∂α／∂ｙ
と表すことが出来ます。

　ここで、スカラーα（ｘ、ｙ）の分布そのものはスカラー量ですが、ベクトルＡ（ｘ、ｙ、ｚ）の各成分が
ｘ成分＝Ａｘ＝Ｃ、
ｙ成分＝Ａｙ＝Ｃ、
ｚ成分＝Ａｘ＝α
であるベクトルＡを考え、（Ｃは定数）

　このベクトルＡを流線関数ベクトルと呼ぶことにします。

　流れに発散が無ければ（∂ｕ／∂ｘ＋∂ｖ／∂ｙ＝０）、その流れの成分が（−ｖ＝∂α／∂ｘ、ｕ＝∂α／∂ｙ）で与え られるような関数αが存在します。

５）式がαが存在するための必要十分条件であると言うことは、逆に、流れに発散があればその微分が流れを現すような関数α は存在しないことも言っています。

＜３−３＞　流れの分類

　以上の二つの流れの検討から、流れを次の４つに分類する事ができます。

　１つ目は、流れの中に渦も発散も無い流れで、これには速度ポテンシャルと流線関数が共に存在します。

２つ目は、渦のみがあって、発散の無い流れの場合で、これには流線関数のみが存在します。

３つ目は、発散のみがあって渦の無い流れの場合で、これには速度ポテンシャルのみが存在します。

４つ目は渦と発散が共に有る場合で、これには流線関数も速度ポテンシャルも存在しません。この流れが一般的で、現実には 多く存在していると考えられます。

　このことを図に示しますと下図のようになります。

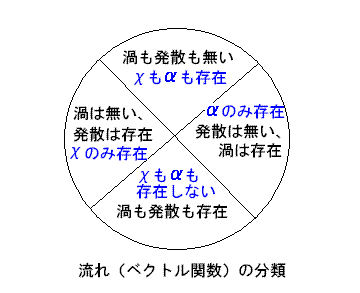
　従って、基本的には、流れに渦と発散のある場合は、元の流れには流線関数も速度ポテンシャルも存在しませんから、 これらの関数を用いて流れが分解できるという「ヘルムホルツの分解定理」は間違っています。

この簡単な分類が、世の流体力学の偉い先生方には理解できないのです。100年も言われてきているから、正しいと信じて、 自分の頭では考えないのです。今得ている権威が損なわれる恐れのあることには同調できない情けない連中だと私は思います。

彼らの言い分は、「渦も発散もある流れを、χのみとかαのみで表すことができないと言うことだけで、分解して分けて考える と両方存在するのだ」とか、「＜４−１＞、＜４−２＞はどちらかがゼロの時にポテンシャルが存在することを証明しているだ けであって、両方ともゼロでない時にポテンシャルが存在しないことを証明した訳ではない」といいます。

必要十分条件のことがよく分かっていないか、一つの事象に独立して存在する二つの条件があったときの考え方が非常に幼稚 なかのどちらかでしょう。

必要十分条件について、もっと分かりやすい例を上げて、説明いたします。

流れの総てを入れ物に例えます。

この入れ物は、球形（渦のある流れ）か立方体（渦の無い流れ）の2種類しかありません。又、色は黒（発散のある流れ）か赤 （発散の無い流れ）しかありません。

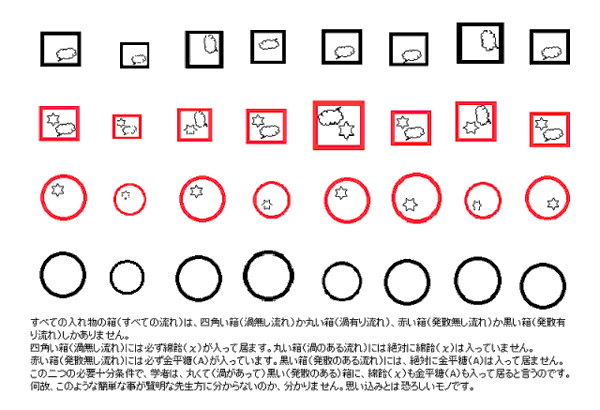
ここで、総ての立方体の入れ物（渦が無い流れ）には、綿飴（速度ポテンシャル）を入れ、総ての球体の入れ物（渦が有る流れ） には綿飴が入っていない事を確認します。

また、総ての赤い入れ物（発散が無い流れ）には、金平糖（ベクトル関数＝流線関数）を入れ、総ての黒い入れ物（発散が有る 流れ）には金平糖が入っていないことを確認しておきます。

これだけの作業をした後、あなたは、球体で黒い入れ物に綿飴と金平糖が入っていると考えますか。私には、明言できます。 黒くて球体の入れ物には、綿飴も金平糖も入って居ないことを。

この入れ物の例えは、全く流れの分類の事実と本質的に変わる所が有りません。

気象学者や流体学者は、この入れ物の例えで言いますと、黒くて球体の入れ物に、綿菓子と金平糖が両方とも入って居ると言い 切るのです。

あなたは、どう思います？

＜４＞ ベクトル3重積の持つ意味

ベクトル3重積の展開とは



と示されるベクトルの恒等式です。この恒等式を用いて
ベクトルAとベクトルBをともに


で置き換え、ベクトルCをベクトルWで置き換え、適当な移行を行うと

・・・・・１）

となります。

ここで、∇・Ｗはスカラー量ですから、スカラーχとおき、∇×Ｗは ベクトル量ですからベクトルＡと起き、
−∇^２Ｗ＝Vとおくと、

・・・・・２）

となります。

すなわち、この式でもって、"任意の”ベクトルV”が、渦の無いベクトル∇χと 発散の無い∇×Ａに分解されると考えるのが 「ヘルムホルツの分解定理」です。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

しかし、任意のベクトルとして扱われて居る−∇^２Ｗは、実は 任意のベクトルではありません。

展開の途中経過にご注意下さい。渦の無いベクトルを導き出しているχと、発散の無いベクトルを導き出しているＡはともに、共通の Ｗと言うベクトルに由来しています。

同じベクトルWから生まれているため、互いに他に影響を受け、互いに独立である とは言えません。一方が決定されると、必然的に他方も決定される関係にあります。

もう少し、具体的に−∇^２Ｗが任意のベクトルと考えると矛盾が 生じることを示しましょう。

　ベクトル関数V₁を、χ₁と、Ａ₁からなるベクトルとし、 ベクトル関数V₂を、χ₂と、Ａ₂からなるベクトルとします。

　「ヘルムホルツの分解定理」によると、任意の流れ（ベクトル関数）は任意の渦成分流れ （∇×Ａ）と任意の発散成分流れ-（∇χ） の組み合わせが考えられる筈ですので、渦なし発散流れ成分が-（∇χ₁）で、 発散無し渦流れ成分が（∇×Ａ₂）である流れ V₃を考えます。

すなわち、 V₃＝-∇χ₁＋∇×Ａ₂
です。

ここで 　χ₁＝∇・Ｗ₁ 　Ａ₂＝∇×Ｗ₂ です。

従って、V₃＝-∇（∇・Ｗ₁）＋∇×（∇×W₂）

　χ₁とＡ₂の組み合わせでできたベクトルV₃ に１）式を適用すると、

となりますが、この時V₃は、V₁とも V₂と違いますので、

です。 従って、 V₃≠V₃

と言う矛盾した結果になります。 　

　このような組み合わせは、無限に考えられ、一般にヘルムホルツの分解が成り立たないベクトル場 が無限に存在することを示して居ます。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

このベクトル3重積が成り立つのは、電磁波に見られる電界と磁界のばあいのみです。

Wikipediaなどに「ヘルムホルツの分解定理」を記述している人の多くは、電磁気関係の人が多いようです。 彼らは、ヘルムホルツの分解定理」を信じていますが、本来電気時に「分解定理」は不要です。

べくトル3重積は、一つの電磁波（光やガンマ線も含んで）に対して成り立って居るだけで、 任意の電磁波の電界と磁界が任意に組み合わされるわけではありません。

例えば、朝日放送の電波の電界と毎日放送の電波の磁界の組み合わせなどはありようもありません。

ヘルムホルツの分解定理とは、そのような電波も考えられるといっているのです。

ベクトル3重積の示す意味は、電界から基本電荷が得られる力と磁界から基本電流が 得られる力が直交しており、それらの電界と磁界を合成することのできるあるベクトルが考えられる、 と言う事を言っています。分解定理と言うよりは特殊合成定理と解釈すべきです。

私がもう少し若ければ、この合成ベクトルが何なのか調査してみたいのだが、 ちょっと気づくのが遅すぎました。電磁波が何故飛び続けられる のか、不思議と言えば不思議です。

電磁波が何故飛んでいくのか、分かったようなことを書いていて居る人も、本当は分かっていないのかも知れません。