That Sneaky Exponential Beyond Metcalfe's Law to the Power of Community Building	Cat: ICT Pub: 1999 #:9905b
	David P. Reed

Title	"That Sneaky Exponential" : - Beyond Metcalfe's Law to the Power of Community Building -	ネットワーク価値のべき乗的増大: - メトカーフの法則を超えるコミュニティ構築 -
Author	David P. Reed	デビッド・Ｐ・リード
Published	1999	1999年
Index	Value of the network: Powerful bonus:	ネットワークの価値: 強力な付加価値:
Why this report?	Dr. Reed is a consultant and entrepreneur who believes the best way to predict the future is to build it, also who smartly describes value of the network, and shift of the core applications. Also this is a continuation story of "externality of the network." Let's untwist twined and twisted market of the network.	Dr. Reedは、未来を予測する最良の方法はそれを作ることだという信念をもつコンサルタント・起業家であり、ネットワークの価値およびその中心となるアプリケーションの変遷をうまく表現している。 これはまた「ネットワークの外部性」の話の延長でもある。ネットワークの絡み合って混乱している市場をほぐそうではないか。

Summary	要約
>Top 1. Value of the network: Bob Metcalfe, inventor of the Ethernet, points out that the value of communications network grow with the square of the number of devices or people it connects: $(N^2)$ This implies value grows faster than does the linear number of a network's access points. <Externality of Network> Some network structures create total value that can scale even faster than that. Networks that support the construction of communicating groups create value that scales exponentially with network size, i.e. much more rapidly than Metcalfe's square law. I will call such networks Group forming Networks (GFN). Metcalfe's law says that if you build a network so that any customer can choose to transact with any other customer; the number of potential connections each of the N customers can make is $(N-1)$, giving a total number of potential connections as $N(N-1)$ or $N^2-N$. Assuming each potential connection is worth as much as any other, the value to each user depends on the total size of the network, and the total value of potential connectivity scales much faster than the size of the network, proportional to $N^2$.	１．ネットワークの価値： イーサーネットの発明者であるボブ・メトカーフは、通信ネットワークの価値はそれに接続された機器あるいはそこに接続する人々の数の二乗に比例することを指摘した。$(N^2)$ これは、ネットワークの価値が、アクセスポイントの直線的な増加より早いことを意味する。(ネットワークの外部性) いくつかのネットワークのインフラはネットワークそのものより早いスケールで価値を生み出すことができる。コミュニティ・グループをサポートするネットワークは、ネットワークの規模の指数関数的に価値が増大する。つまり、メトカーフ法則の二乗よりずっと早いのだ。このネットワークをGroup forming Networks (GFN)と呼ぶ。 メトカーフの法則とは、ネットワークが作られるどの顧客も他の顧客と交信できる。$N$人の顧客ネットワークの交信の可能性は$N-1$で、全体では$N(N-1)$、即ち$N^2-N$となる。 どの交信も他と同じ価値があるとすれば、その価値はネットワークの規模に依る。その価値の合計はネットワークのサイズよりもずっと速く、$N^2$に比例する。
>Top At this point a skeptic once said that's too simplistic, that's not the most important source of value in the network like the phone network. For example, there's a weather service that everyone calls once a day, and the 911 service, and a couple of other services like that. And each user typically has a fixed, small set of friends and family that they call all of the time. Since the value of these services to a particular user does not depend on the number of other users of the network, the total value of these services grows more slowly―proportional to $N$, not $N^2$. To illustrate this, let's assume that we can lump all of the kinds of value that grow proportional to $N$ in one term, which we can write by the formula $aN$, where $a$ is a constant that represents the value per customer. We can also represent the value of potential connectivity by $bN^2$, where $b$ is the constant value of a potential connection between a pair of customers. Let's assume that $b$ is much smaller than $a$, so that for a modest size network, the total network value is for all intents and purposes the same as $aN$ But still, if we allow $N$ to get large enough, the total network value will get closer and closer to $bN^2$. Thus, the "square" value of potential connectivity dominates all linear sources of value once $N$ gets sufficiently large.	ここで懐疑的な人はかつてこう指摘した。それではあまりにも単純すぎる、と。電話のようなネットワークの価値はそのような価値にあるのではなくて、一日に１回誰でも電話で天気予報を聞くサービスがあるし、緊急電話110番などのサービスもある。さらにどのユーザも限られた範囲の友人や家族といつも電話しているのだ。これらのサービスの価値はネットワークの他人の数には依存しないし、サービス価値はもっと緩慢に（$N^2$ではなく) $N$に比例して増えていく。 これを式にしてみよう。 $N$の数に比例して増加する価値の合計を$aN$で表すとしよう。ここで $a$ は、ユーザにとっての価値を表す定数とする。 ネットワーク接続による価値を $bN^2$とする。ここで$b$ は、交信するユーザにとっての価値の定数とする。$b$は$a$よりずっと小さいと仮定する。そこそこの規模のネットワークの場合、全ネットワークの価値 $an + bN^2$ は事実上は$aN$と同じになる。しかし、$N$が十分大きい場合は、全ネットワークの価値は$bN^2$に限りなく近づいてくる。こうして$N$が相当大きければ、一次元的に増加する交信可能性の二乗となる。
>Top In networks like the Internet, Group Forming Networks (GFNs) has functionality that directly enables and supports affiliations (such as interest groups, clubs, meetings, communities) among subsets of its customers. Group tools and technologies (also called community tools) such as user-defined mailing lists, chat rooms, discussion groups, buddy lists, team rooms, trading rooms, user groups, market makers, and auction hosts, all have a common theme―they allow small or large groups of network users to coalesce and to organize their communications around a common interest, issue, or goal. Sadly, the traditional telephone and broadcast/cable network frameworks provide no support for groups. GFNs create a new kind of connectivity value that scales exponentially with $N$. Briefly, the number of nontrivial subsets that can be formed from a set of N members is $2^N-N-1$, which grows as $2^N$. Thus, a network that supports easy group communication has a potential number of groups that can form that grows exponentially with $N$. 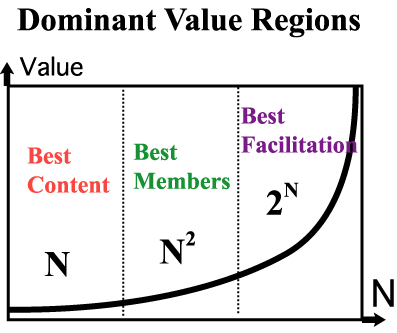The exponential, $2^N$, is a sneaky function. Though it may be very small initially, it grows much faster than $N^2, N^3$ or any other power law. So if there is any portion of the total network value that grows exponentially, scale effects will eventually bring that value to the fore, where it will dominate any other source of value. To put it simply, if a network's value consists of components that scale proportional to $N, N^2$, and $2^N$, we can write the total value as where $a, b,$ and $c$ are constants. As long as $a, b, $and $c$ are positive, there will be some M such that the total value is dominated by the term $c2^N$ for all $N>M$. Even if $c$ is quite small, the exponential will eventually dominate. $aN+bN^2+c2^N$	インターネットのようなネットワークでは、グループ作成ネットワーク（GFN）は、顧客の部分集合としてのグループ団体（インタレストグループ、クラブ、会議、コミュニティーなど）を直接支援する機能を持つ。ユーザを定義するメールリスト、チャット・ルーム、会議グループ、仲間・チームグループ、取引ルーム、ユーザグループ、市場作成、オークション運営などのグループ・ツールや技術（コミュニティーツールと呼ばれる）はすべて共通の目標を持つ。即ち、ネットワークの大小のグループを合体し、関心事項や目標達成のためのコニュニケーションを行う。従来の電話、放送、CATVには全くこのようなグループを支援することは用意されていない。 GFNは、加入者数$N$に応じて指数関数的に接続の価値を作りだす。要するに、非自明の部分集合の数は集合Ｎに対し、 $2^N-N-1$であり、グループ・コニュニケーションを支援するネットワークは、$N$が大きくなると指数関数的にそのグループの可能性を拡大し、$2^N$に近づく。 (左図参照) この指数関数的な$2^N$という数は不可思議である。最初は非常に小さいが、$N$に従って、$N^2$や$N^3$などのベキ乗数よりもずっと早く大きくなる。それゆえ、もしネットワークの価値のある部分が指数関数的に増加するとすれば、規模の効果は際立ってくることになる。 要するに、ネットワークの価値の合計は: $aN+bN^2+c2^N$ （ここで$a, b, c$は定数） a, b, cが正数である限り、ある一定加入者$M$以上の$N$についての全ネットワークの価値は、たとえ、$c$が小数としても、$c2^N$で規定される。
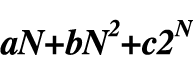
>Top 2. Powerful bonus: Both laws give a powerful bonus to interconnection; mergers and partnerships of networked companies should be able to extract a premium resulting from these laws. When we combine two networks together so that users of one network can connect seamlessly to users of the other, Metcalfe's Law tells us already that substantial new value is created: $(M+N)^2 = M^2 +N^2+2MN$. This bonus term, 2MN, is substantial-up to 100% of the value in the original unconnected networks. Thus there is an enormous incentive to find ways to interconnect networks, since the members of each network can access a much larger set of potential transaction partners. With the GFN law, interconnection is even more powerful, creating many new potential groups that span the two networks: 2^{M+N}= 2^M \times 2^N$2^(M+N). The GFN interconnection bonus percentage itself grows exponentially with the size of the smaller network. There are really at least three categories of value that networks can provide: the linear value of services that are aimed at individual users, the "square" value from facilitating transactions, and exponential value from facilitating group affiliations. What's important is that the dominant value in a typical network tends to shift from one category to another as the scale of the network increases. In a network dominated by linear connectivity value growth, "content is king." That is, in such networks, there is a small number of sources (publishers or makers) of content that every user selects from. The sources compete for users based on the value of their content (published stories, published images, standardized consumer goods). Where Metcalfe's Law dominates, transactions become central. The stuff that is traded in transactions (be it email or voice mail, money, securities, contracted services, or whatnot) are king. And where the GFN law dominates, the central role is filled by jointly constructed value (such as specialized newsgroups, joint responses to RFPs, gossip, etc.).	２．強力な付加価値： ネットワーク関連企業同士の提携、合併、パートナーシップによって、この法則による強力なメリットが得られる。 ２つのネットワークが提携する場合、他のネットワークユーザとシームレスに連結でき、メトカーフの法則によって得られるネットワークの価値は、 $(M+N)^2 = M^2 +N^2+2MN$となり、提携前の両者の価値の合計よりも、$2MN$ 相当分だけ価値が増大する。このことはネットワークの提携のもたらす大きなインセンティブであり、各々のネットワークのメンバーはずっと大きな取引可能性のあるパートナーにアクセスできるのである。 GFNの法則によれば、提携はもっと強力となり、グループの可能性の価値増大は、 $2^{M+N}= 2^M \times 2^N$となる。GFNの提携の価値は、より小さなネットワークの規模の指数関数的に増大していく。 ネットワークが提供できる価値の増大には３つの階層がある。ここのユーザを対象にした一次元の価値、ユーザ間取引による二次元の価値、そして様々なグループ関係を作りだす指数関数的な価値である。重要なことは、ネットワークの規模の増大にともなって、支配的な価値がある種類から別の種類に移ることである。 一次元の接続による価値の増大が主なネットワークにとっては、「コンテンツは王様」である。このようなネットワークでは、どのユーザも利用する少数の情報源（出版社や制作者）がある。情報源はその中身の価値（出版されるストーリ、イメージ、標準的な消費者グッズ）によってユーザ獲得を競い合う。 メトカーフの法則の支配する所では、取引が中心である。この場合は、取引に使用される要素（電子メール、ボイスメール、貨幣、証券、契約サービス等々）が王様である。 GFNの法則が支配する所では、中心的な役割は、共同で構築される価値にある。即ち、特定のニュースグループ、RFPに対する共同意見、ゴシップ等である。
>Top Several cases: The Internet auction pioneer, OnSale, is based on a business model that scales linearly, proportionally to the reach of its network. OnSale buys closeout products and auctions them to anyone who can access its website to present a bid. In return, OnSale gets margin on every sale. Online classifieds, which connect buyers to sellers on a peer-to-peer basis, would seem to create a market space whose value follows Metcalfe's Law. We'd expect to see a shift of dominance from OnSale to online classifieds once the network tools for safe peer transactions can be made to work. But the newly public company eBay seems destined to capture a scale shift to the exponential logic of GFNs in creating value for its members. eBay's concept is to help its members to set up specialized auction communities on its website as buyers and sellers of many kinds of collectibles, art, and other easily traded special interest goods. Though eBay's share of the transactions it facilitates is much smaller than OnSale's share, eBay's returns can increase much more rapidly with scale. This growth in returns will be driven by an exponential growth in value of the eBay GFN as its membership increases. Scale driven value shifts have already caused Lotus to incorporate features into Notes/Domino to interconnect in a limited way with the faster-growing Internet. But Notes' enterprise focus makes it difficult to support ad hoc groups that live outside large enterprise boundaries or span multiple enterprises. Though the email capabilities of Notes can easily interconnect with other Internet email systems across boundaries to capture a fair share of Metcalfe's Law value as the Internet grows, Lotus has chosen an enterprise-oriented model for sales and an enterprise focused security model. That choice effectively limits GFN reach to a few islands scattered throughout a vast Internet.	いくつかの事例： インターネット・オークションの創始者であるOnSaleのビジネスモデルは、ネットワークで接続できる人に比例、即ち一次元的である。 OnSaleは、見切り商品を購入し、Web上で公開の入札を行う。OnSaleは、各々の売上に対しマージンを取得する。メンバー間同士で（P2P的に）買い手と売り手を結びつけるオンライン案内広告のやり方は、メトカーフの法則に従う市場の価値を作り出すように見える。メンバー間の安全な販売のためのネットワーク・ツールが一旦機能し始めると、OnSaleから広告案内へと中心が移動することが期待できる。 しかし新たに上場したeBayの場合は、メンバーに対しGFN的な指数関数的な価値に移行することを予定していたかのように見える。 eBayの概念は、メンバーに対しWeb上で、種々の収集品、芸術品その他容易に取引されるような興味を引く商品の買い手と売り手を集めた特別なオークション・コミュニティを作ることにある。 eBayの取引シェアは、OnSaleのシェアより小さいが、規模増大に伴いeBayの収入はずっと早く増加する。この増加は、eBayのGFNメンバーシップの増加によってもたらされる。 規模によってもたらされる価値のシフトはすでにLotus Notes/Dominoの特徴に一定程度はインターネット対応として反映されている。 但し、Notesの製品で企業外あるいは企業間のアドホック・グループをサポートするのは困難である。 Notesの電子メールは、企業外の電子メールシステムの連携能力がありインターネットの成長というメトカーフの法則は捉えているが、Lotusは、企業中心の販売および セキュリティモデルを想定している。 この想定モデルでは、広大なインターネットに散在しているグループに対しGFN的に対応することには限界がある。
>Top Thus scale driven value seems likely to shift dominance to new groupware products and business models that can capture exponential value growth by enabling all Internet users to affiliate flexibly. By facilitating easy ad hoc creation of "teamrooms", Instinctive's eRoom and Excite's Excite Communities, among others, seem likely to capture big shares of a scale driven value shift from email to ad hoc project team collaboration. There will be many more ways that we'll see scale driven value shifts that threaten established business networking patterns. For example, health care networks may move from treatment transactions to collaborations around disease management. Risk management in the financial services sector may move to group-forming structures that facilitate management of "micro-risks". Speculative thought: There is a strong correlation between the prosperity of national economies and social capital, with which people in a particular culture can form new associations. There is a clear synergy between the sociability and the technology and tools that support GFNs-both are structural supports for association. As the scale of interaction grows more global via the Internet, a combination of social capital and GFN capital will drive prosperity to those who recognize the value of network structures.	今後の傾向は、指数関数的な価値増大を捉えるような新たなグループウェアやビジネスモデルに移行していき、インターネットユーザともっと柔軟に提携できるようないなる。Instinctive's eRoom社の"teamrooms"や、Excite社のExcite Communitiesなどは電子メールからアドホックプロジェクトチームの協業という価値の変化をうまく捉えようとしている。 規模による価値シフトは既存のビジネスネットワークの脅威となりつつある。 ヘルス・ケア分野：診療から病気管理協業への動き リスクマネジメト分野：金融サービスでは「マイクロリスク」管理を提携するグループ創生へと移行する動き。 推論： 国民経済の繁栄度と社会資本とは強い関連性がある。それによって特定の文化を担う人々の間で新たな提携を作ることができる。 GFNをサポートする交流・技術・ツールの間の明らかな相乗効果は、グループ活動の組織的な支援となる。 相互の関係がインターネットを通じて更にグローバルなるに従って、社会資本とGFN資本との組合せによってネットワーク構造の価値を認識する人に対し利益をもたらすことになろう。

Comment	>Top This thesis is recommended by iCivil study group, hosted by Prof. S. Kumon, executive director of GLOCOM, International Univ. of Japan.	この論文は、国際大学GLOCOMの公文俊平所長主催のicivil研究会推薦の論文である。