$\cong$	Note of Group Theory - Theory and Application -	Cat: SCI Pub: 2020 #2020a
	Yobinori (YouTube)	20z19u

Title	Note of Group Theory	群論入門ノート
Index	Preface: Group Theory: Definition of Group: Symmetric Group: Subgroup: Equivalence Class: Residue Class (Coset): Normal Subgroup: Homomorphism: Fundamenta Homomorphism Theorem: Hasse Diagram:	序文: 群論入門: 群の定義: 対称群: 部分群: 同値類: 剰余類: 正規部分群: 準同型写像: 準同型定理: ハッセ図:
Tag	; Associative law; Bijective; CAII; Equivalece class; General Linear group; Group definition; Hasse diagram; Homomorphic; Identity permutation; Inverse element; Isomorphism; MECE; Neutral element; Non-commutative; Normal matrix; Operation; Permutation; Quotient group; Subgroup; Symmetry; Symmetric group; Transition; Trivial group;

Original resume

Remarks

>Top 0. Preface: Set Theory: is a well-defined collection of objets. Set Operations: $a\subset A$ $\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R} \subset\mathbb{C}$ $A=B \Leftrightarrow A\subset B$ and $B\subset A$ disjoint: $A\cap B=\emptyset$ complement: $A'=\{x\!: x\in U\ \text{and}\ x\notin A\}$ difference: $A \verb|\| B=A\cap B'=\{x\!: x\in A\ \text{and}\ x\notin B\}$ De Morgan's Law: $(A\cup B)'=A'\cap B';\; (A\cap B)'=A'\cup B'$ >Top Cartesin Products and Mappings: onto or surjective: if $f:A→B$ i.e., $f(A)=B$ 全単射, bijective: =one-to-one correspondence/onto mapping compositon: $(g\circ f)=g(f(x))$

0. 序文: disjoit: 互いに素, 共通元なし

>Top 1. Group Theory: 集合の上に演算 (加算、積算など)考える (=代数系) 必要最低限のルール: 結合法則: $(a \circ b)\circ c=a\circ(b\circ c)$ 群(group)、環(ring)、体(field): (演算2つ；ルールの数が増える) 群〜体: Galois理論; 5次以上代数方程式の一般解なし 複素数のseki 複素数の積: ¶集合 {i, -1, -i, 1} の群の構造 (群表) 行列の積: $\pmatrix{0&-1\\1&0}\pmatrix{-1&0\\0&-1}\pmatrix{0&1\\-1&0} \pmatrix{1&0\\0&1}$ →$\pmatrix{\cos\theta&-\sin\theta\\\sin\theta&\cos\theta}$ →$\frac{\pi}{2},\; \pi,\;\frac{3\pi}{4}.,\; 0$ の回転操作に相当 (代数的同型) 群の表現: 群(元、演算):→正則行列の積 (一般線形群)[準同型写像；準同型定理の理解] 対称性: ある変換に対して不変 (=通常、群という →結晶構造や波動関数の分類

1. 群論入門:   a b c d a b c d a b c d a b c d a b c d a b c d $\pmatrix{0&-1\\1&0}$

>Top 2. Definition of Group: 定義 (群, Group): 集合G ($\ne \emptyset$)に対して二項演算(binary operation; "$\circ$") $G\times G\mapsto G$ $(a,b) \mapsto a\circ b$ が与えられていて、以下の条件(C,A,N,I)を満たす時、Gを群という。 演算に対して閉じていること(Closure condition) 結合法則(Associative law): $ \forall a, b, c\in G$に対して $(a\circ b)\circ c=a\circ(b\circ c)$が成り立つ。 単位元(Identity/Neutral element)の存在: ある$e\in G$が存在し、$\forall a\in G$に対して$a\circ e=e\circ a=a$を満たす 逆元(Inverse element)の存在: $\forall a\in G$に対して$a\circ b=b\circ a=e$を満たす$b\in$が存在する。 >Top ¶群の条件 (演算 operationとセットで考える): [C, A, I, I]; 論理演算子logical operator $(\mathbb{R}, +)$ [○,○,○,○] $(\mathbb{Z}, +)$ [○,○,○,○] (0の逆元は0) $(\mathbb{R}, \circ)$ [○,○,○,☓] $(\mathbb{R^*}, \circ)$ [○,○,○,○] (0以外の実数) $(\mathbb{T}=\{z\in\mathbb{C}||z|=1\}:$ $(\mathbb{T},\circ)$ [○,○,○,○] (=$e^{i\theta}$) $G={1}$; 自明群 (trivial group) $(G,\circ)$ [○,○,○,○] $G=\{i, -1, -i, 1\}$ $(G, \circ)$ [○,○,○,○] $\mathbb{R}$上のn次正則行列全体は、行列の関会長殿に関する群 →$GL_n(\mathbb{R})$ (General Linear Group, 一般線形群) →正則行列, regular matrix; non-singular; invertible: 注: $\forall a,b\in G$に対して$a\circ b=b\circ a$を満たすとき$G$を可換群(commutative group or Abelian group)という。[群の定義ではない] なお、有限群(finite grouop)と無限群(infinite group)がある。 群$G$の元の個数をその位数(order)といい、$|G|$で表す。 以降、$a\circ b$を$ab$と省略する。→掛け算でなくても積(product)という。 >Top 定理: 群$G$に対し、単位元(Identity/Neutral element)はただ１つ存在する。 $\forall a\in G$に対し、逆元はただ一つ存在する。 証明: 単位元を$e,\;e'$とする。 $\cases{ee'=e'\; (e\text{は単位元})\\ee'=e\;\; (e'\text{は単位元})}$ →$e=e'$ (uniqueness of neutral element) $a$の逆元を$b,\;b'$とする。→$b=eb=(b'a)b=b'(ab)=b'e=b'$ (uniqueness)→$a^{-1}$と書く。$...\Box$ 注: $(a^{-1})^{-1}=a$ ∵ $aa^{-1}=a^{-1}a=e\;→(a^{-1})^{-1}=a...\Box$ [$a^{-1}=c$とみると$a=c^{-1}=(a^{-1})^{-1}$] $(ab)^{-1}=b^{-1}a^{-1}$ ∵ $(b^{-1}a^{-1})ab=b^{-1}(a^{-1}a)b=b^{-1}b=e$ $ab(b^{-1}a^{-1})=a(bb^{-1})a^{-1}=aa^{-1}=e$ →$b^{-1}a^{-1}=(ab)^{-1}$

2. 群の定義 群の定義: CAII

>Top 3. Symmetric Group 定義: 対称群 (symmetric group); 置換(permutation) $\Omega_n=\{1,2,\cdots,n\}$として$\Omega_n$から$\Omega_n$への全単射(bijection)全体の集合を$S_n$とおく。$S_n$は写像の合成に関して群となる。この群$S_n$をn次対称群という。 ¶$S_3$ [最初は恒等置換(identity permutation)] $\dbinom{1\ 2\ 3}{1\ 2\ 3}(\rho_0=e)\;\dbinom{1\ 2\ 3}{2\ 3\ 1}(\rho_1)\;\dbinom{1\ 2\ 3}{3\ 1\ 2}(\rho_2)$ $\dbinom{1\ 2\ 3}{1\ 3\ 2}(\mu_1)\;\dbinom{1\ 2\ 3}{3\ 2\ 1}(\mu_2)\;\dbinom{1\ 2\ 3}{2\ 1\ 3}(\mu_3)$ 演算: $\rho_2\mu_1=\underleftarrow{\dbinom{1\ 2\ 3}{3\ 1\ 2}\dbinom{1\ 2\ 3}{1\ 3\ 2}}=\dbinom{1\ 2\ 3}{3\ 2\ 1}=(\mu_2)$ 演算: $\mu_1\rho_2=\underleftarrow{\dbinom{1\ 2\ 3}{1\ 3\ 2}\dbinom{1\ 2\ 3}{2\ 1\ 3}}=\dbinom{1\ 2\ 3}{3\ 1\ 2}=(\rho_2)$ 逆元: $(\rho_1)^{-1}=\dbinom{2\ 3\ 1}{1\ 2\ 3}=\dbinom{1\ 2\ 3}{3\ 1\ 2}=(rho_2)$ ¶$S_1=\bigl\{\binom{1}{1}\bigr\}=e$ ¶$S_2=\bigl\{\binom{1\ 2}{1\ 2},\binom{1\ 2}{2\ 1}\bigr\}$ >Top 注: $S_n\; (n≥3)$は非可換群(non-commutative group) $|S_n|=n!$ 任意の置換は互換の積で表される。>* $S_{10}=\sigma=\binom{1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9\ 10}{6\ 8\ 5\ 4\ 2\ 10\ 9\ 3\ 7\ 1} =(1\ 6\ 10)(2\ 8\ 3\ 5)(7\ 9)=(1\ 10)(1\ 6)( 2\ 5)(2\ 3)(2\ 8)(7\ 9) $ 互換積は一意的ではないが、互換の数は偶数か(偶置換 even permutation)、奇数か(奇置換 odd permutation)は一意的に決まる。 対称群とは"ものを並び替える操作"を元とする群である。 Symmetric group defined over any set is the group whose elements are all the bijections (=one to one correspondence) from the set to itself, and whose group operartion is the composition of functions.

3. 対称群」: *(2\ 8\ 3\ 5)=( 2\ 5)(2\ 3)(2\ 8) 2を固定し後ろから互換

>Top 4. Subgroup: 定義 (部分群, subgroup): 群$G$の空でない部分集合$H$が、$G$の二項演算(binary/dyadic operation)によって群になるとき、$H$を$G$の部分群といい、$H≤G$と表す。 ¶例: $(\mathbb{Z*},+)≤(\mathbb{Q},+)≤(\mathbb{R},+)≤(\mathbb{C},+)$ $SL_n((\mathbb{R})≤)≤GL_n((\mathbb{R})≤)$ $SL_n((\mathbb{R},+) (detA=1); GL_n((\mathbb{R},+) (detA≠0)$ $E\in SL_n(\mathbb{R});\; A^{-1}\in SL_n(\mathbb{R})$ $\{e\}≤Ǧ;\; G≤G$ [自明な部分群] 注: $H$ (e')と$G$ (e)の単位元は一致する。 ∵ $e'$の$G$における逆元$x\in G$をとると、 $e'x=xe'=e$ →e'=(xe')e'=x(e'e')=e $H$と$G$の逆元は一致する。 ∵$c\in H$の$H$での逆元$c'$と$G$での逆元$x$を考える。 $c'=c'e=c'(cx)=(c'c)x=ex=x$ >Top ¶定理: 群$G$の空でない部分集合$H$に対し、 $H$は$G$の部分群⇔$\forall a,b\in H,\; a^{-1}b\in H$ [部分群判定定理] ∵ ⇒側は自明: $a, b, a^{-1}b$も$H$の中に入っている よって[但し、$a^{-1\in H}$は必ずしも成立するとはしていない。] $H≠\emptyset$より、$a\in H$がとれ、 N: $a\in H$より、$a^{-1}a=e\in H$ [$e$が$H$の中にある] I: $a, e\in H$より、$a^{-1}e=a^{-1}e\in H$ C: $a^{-1}b\in H$に対し、$(a^{-1})^{-1}b=ab\in H$ A: $H$が$G$と同じ演算について、閉じているのは明らか $...\Box$ 注: 準同型写像$f$が、逆写像$f^{-1}$を持ち、かつ$f^{-1}$もまた準同型(homomorphic)であるとき、$f$は同型写像(isomorphic)であるという。

4. 部分群: 部分群: Divide & controlのため 二項演算: ２つの数から新たな数を決定する法則; 加減乗除を一般化 n次特殊線形群 準同型: 構造的に同型を保つ写像; 構造を保存(structure preserving)、構造と可換(commute with strucuture)である。 同型: 構造的に全く同じ場合

>Top 5. Equivalence Class: 定義: 同値関係: 集合$S$において、関係〜が定義されていて、2元$x,y\in S$に対し、$x\sim y$であるか、または$x\nsim y$のいずれかが成立し、かつ次の3条件を満たす時、関係〜を同値関係(equivalence relation)という。 反射率(reflective) $x\sim x$、 対称律(symmetric) $x\sim y$ならば$y\sim x$ 推移律(transitive) $x\sim y\cap y\sim z$なら、$x\sim z$ =は同値関係 >は反射率が満たされない ≥ 対称律が満たされない 定義; 同値類 〜を集合$S$上の同値関係とする。$x\in S$に対し、 $C(x)=\{y\in S|x\sim y\}$を$x$の同値類(equivant class)という。 定理: 被りがないことを保証する定理 $\forall y, z\in C(x),]; y\sim z$ $y\in C(x)\Rightarrow C(x)=C(y)$ $C(x)\cap C(y)≠\emptyset \Rightarrow C(x)=C(y)$ 証明: $z\in C(x)$より、$x\sim z$ $y\in C(x)$より$x\sim y$つまり$y\sim x$よって$y\sim z$ $z\in C(x)$をとる [=$C(x)$から適当な要素$z$をとる] $y\in C(x)$より、$y\sim z$、よって上記1.より$z\in C(y)$ [=$z$は$y$の同値類の要素] 故に $C(x)\subset C(y)$...(1) $y\in C(x)$より$x\sim y$つまり$y\sim x$ よって$x\in C(y)$であり、$w\in C(y)$とすると$x\sim w$であり$w\in C(x)$ [=$w$は$C(x)$の要素] 故に $ C(x)\supset C(y)$...(2) (1)(2)により$C(x)=C(y)$ $z\in C(x)\cap C(y)$ [空集合でないので適当な要素$z$をとってくる。] このとき、$C(x)=C(z),\; C(y)=C(z)$ [定理2.より要素自身が同値類の代表元の取替] となるので、$C(x)=C(y)$ $...\Box$ 同値関係による商: [集合$S$の中に、ある〜関係に対応した$C(x), C(y), C(z)$があるとすると、(被りのない)同値類を要素とした集合を考える→同値関係による商$S/\sim$という。]

5. 同値類:

>Top 6. Residue Class (Coset): 定義: 左剰余類 (Left coset) [$G$の部分群$H$を使った同値関係を考える] $H$を群$G$の部分群とする。 $a,b\in G$に対し、$a^{-1}b\in H$となるとき、$a\sim b$と定義する。 これは同値関係であり、$a\in G$の同値類を$a$の$H$による左剰余類という。 $C(a)=\{x\in G|a\sim x\}=\{x\in G|a^{-1}x\in H\}$ [$C_{(a)}$; 同値関係が成立するには、反射率･対称律･推移律が成立する必要がある。] 注: $a, b\in G$に対し、$ba^{-1}\in H$を$a\sim b$の定義としたものを$a$の$H$による 右剰余類という。 $G$が可換群であれば、左剰余類も右剰余類 左: $C(a)=\{x\in G|\;a\sim x\}=\{x\in G|\;a^{-1}x\in H\}$ $=\{x\in G|\;a^{-1}x=h\}=\{ah|\; h\in H\}=aH$ [$a$を左から掛ける] 右: $C(a)=\{x\in G|\;a\sim x\}=\{x\in G|\;xa^{-1}\in H\}$ $=\{x\in G|\;xa^{-1}=h\}=\{ha|\; h\in H\}=Ha$ [$a$を右から掛ける] 同値関係であることの条件: 反射率: $x\in G$なら$x^{-1}x=e\in H\;→x\sim x$ [$a=b=x$を取ってくる] 対称律: $x,y\in G$で$x\sim y$なら$x^{-1}y\in H$ [$H$は部分群なので逆元もHに含まれる\;→$(x^{-1}y)^{-1}=y^{-1}x\in H$ → $y\sim x$ [同値関係の定義により$y\sim x$が成り立つ] 推移律: $x,y,z\in G$で$x\sim y\; y\sim z$なら、$x^{-1}y,\;y^{-1}z\in H$ [$H$は部分群なので積演算で閉じているので、 → $ (x^{-1}y)(y^{-1}z)=x^{-1}(yy^{-1})z=x^{-1}z\in H$ → $x\sim z$] 定理: $\forall a,b\in G,\; |aH|=|bH|$ [集合$aH$や$bH$の個数は等しい] 証明: $\forall a\in G,\; |H|=|aH|$を示せばよい。[$H$を固定して比較する] $f: \; H\longrightarrow aH$ 　$\;\; h\longmapsto ah$ [全単射が成り立てばよい] $H=\{h_1,h_2,h_3,\cdots\}$ $aH=\{ah_1,ah_2,ah_3,\cdots\}$ [全射は明らかだが、単射を調べる; $a≠b→f(a)≠f(b)⇔f(a)=f(b)→a=b$] [$ah_i=ah+j$のとき、$a^{-1}ah_i=a^{-1}ah_j\;→h_i=h_j$→]単射である $...\Box$ $G$のHによる左類別: $G=H\cup aH\cup bH\cup\cdots$ 同様に、$G=H\cup Ha\cup Hb\cup\cdots$ [$G$のHによる右類別] [全射は、Hの部分群が全部あるので成立する。後は単射を調べる] $a≠b$ならば$f(a)≠f(b$、即ちその対偶contrapositonである $f(a)=f(b)$ならば$a=b$を示せばよい。 $ah_i=ah_j$\;→$a^{-1}ah_i=a^{-1}ah_j\;→$h_i=h_j$ [単射である] $\;→G=H\cup aH\cup bH\cup\cdots$ [$G$の$H$による左類別] $\;→G=H\cup Ha\cup Hb\cup\cdots$ [$G$の$H$による右類別] この$H$を用いた同値関係による商(=同値類を要素とした集合)の表現: $G/H:=\{eH, aH, bH, \cdots\}$ $H\backslash G:=\{He, Ha, Hb,\cdots\}$ [商の記号$G/\sim =\{C_{e}, C_{(a)}, C_{(b)},C_{(c)},\cdots\}$] ¶$G=\mathbb{Z},\;H=3\mathbb{Z}$ [整数の整合$G$の部分集合としての3の倍数の集合$H$] $\mathbb{Z}/3\mathbb{Z}=\{0+3\mathbb{Z},\ 1+3\mathbb{Z},\ 2+3\mathbb{Z}\} =\{\overline{0},\ \overline{1},\ \overline{2}\}$ [この場合の演算は加法; 加法演算の場合; この例はmod計算に相当; $aH=ah\{h\in\ H\beta\}$]

6. 剰余類: conversion: 逆 $\neg P→\neg Q$ Inversion: 裏 $\neg P→\neg Q$ contrapositon: 対偶 $P→Q$ is $\neg Q→\neg P$ negation: 否定 $\neg(P→Q)$ 群Gについて同値関係を使うと、 (MECE, もれなく被りなく)うまく Group分けを行える。 逆

>Top 7. Normal Subgroup: 定理の前提: $aH･bH=abH$が成立するためには $aH･bH\Rightarrow abH=a'b'H$を満たしていなければならない。 $a'=aH_1,\;b'=bh_2\;(h_1,h_2\in H)$ $\;→a'b'=ah_1bh_2\; (=abh_1'h_2\in abH$となればよい。Hb=bHならOK 即ち$\;→h_1b=Hb,\;bh_1=bH$と書ければOK) 定義 (正規部分群): $H$を$G$の部分群とする。 全ての$a\in G$に対し、$aH=Ha$となるとき、$H$を$G$の正規部分群といい、 $H\trianglelefteq G$と表す。 注: 可換群(communitative group)$G$の部分群(subgroup)は、全て正規部分群(normal subgroup)である。 >Top 定義 (剰余群 quotient group): $N$を$G$の正規部分群とする。 剰余類 $aN$と$bN$の積を $aN･bN=abN$と定義(**)すると、$G/N$はこの演算によって群となり、この群を$G$の正規部分群$N$に関する剰余群という。 証明: 閉じている: 演算の定期から、ok 単位元: $eN$で成立 結合法則: (aN bN) cN=abN cN=abcN=a(bc)N=aN bcN=aN (bN cN) 逆元: $a^{-1}N$ 注: $G$が可換群であれば、$G/N$ (商)も可換群...＊$...\Box$ ¶ 例: $Z/3Z=\{0+3Z,];1+3Zz,\;2+3Z\}$ [Zが可換群→3Zは正規部分群→Z/3Z 正規部分群での商は剰余群となる] 演算: $(0+3Z)+(1+3Z)=(1+3Z)$ [なお中央の+は、上記＊により、剰余群の元同士の演算も可換群となるので+になる。 →代表元同士の演算結果と$N$を書く (上記**)] 演算2: $(1+3Z)+(2+3Z)=(0+3Z)$ [別表記(=mod計算): $\overline{1}+\overline{2}=\overline{0}\;→$mod計算の一般化] 正規部分群の判定法: ${}^\forall z\in G,\;aH=Ha⇔{}^\forall h\in H,\;{}^\forall a\in G,\;aha^{-1}\in H$ 証明$\Rightarrow$: $aH=Ha$より、$ah=h'a$ [$h'a$と書けるように$h'$が存在する] $\;→aha^{-1}=h'\in H$...\Box$ 証明$\Leftarrow$: $aha^{-1}\in H$より$aha^{-1}=h'$ $\;→aha^{-1}a=h'a\in H\;→aH=Ha$ $...\Box$ ¶例: $S_3$ [三次対称群の部分群を考える] $\dbinom{1\ 2\ 3}{1\ 2\ 3}(\rho_0)\;\dbinom{1\ 2\ 3}{2\ 3\ 1}(\rho_1)\;\dbinom{1\ 2\ 3}{3\ 1\ 2}(\rho_2)$ $\dbinom{1\ 2\ 3}{1\ 3\ 2}(\mu_1)\;\dbinom{1\ 2\ 3}{3\ 2\ 1}(\mu_2)\;\dbinom{1\ 2\ 3}{2\ 1\ 3}(\mu_3)$ $→\rho_0,\;\rho_1,\;\rho_2$の部分群は$N$と書ける $→\mu_1,\;\mu_2,\;\mu_3$の部分群は$\mu_1N$ と書ける [正規部分群となるのは$N$だけ] [$\rho_0,\;\mu_1=H$または$\rho_1,\;\mu_2=H$は正規部分群とならない]

7. 正規部分群: 剰余類を元とする群を作る →演算を考える →aH･bH=abHを考える

>Top 8. Homomorphism 定理 (準同型写像): $G,\; G'$: 群 写像 $f: ;G\;→G'$が$f(xy)=f(x)f(y),\;{}^\forall x,y\in G$を満たすとき、 $f$を準同型写像という。[→群の構造を保つ] [写像を考えることで同じかどうか比較する。(=同型)。 この場合、個数のみならず演算も含めての同型かどうか。] $S$が全射の場合 [全射準同型写像 surjective homomorphism] $S$が単射の場合 [単射準同型写像 injective homomorphism] $S$が全単射の場合 [全単射準同型写像 surjective & injective (=bijective 同型写像) homomorphism] $G\cong G'$ 代数構造が全く同じ(近似的意味はない) 定理 (準同型写像): $f(e)=e'$ 証明:\;f(e)=f(ee)=f(e)f(e)\;→f(e)=e'$ [$e$と$ee$は単位元なので同じもの] $f(x^{-1})=f(x)^{-1}$ $f(x)f(x^{-1})=f(xx^{-1})=e'$ 逆に$f(x^{-1})f(x)＝f(x^{-1}x)=e'$ $→f(x^{-1})=f(x)^{-1}$ 定義 (Kernel核、Image像) $G,\;G':$群、$e':G'$の単位元とする。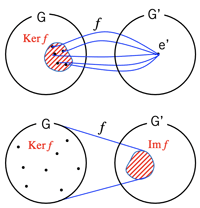 群の準同型写像 $f: G\longrightarrow G'$に対して Ker $f=\{x\in G|f(x)=e'\}$ >Fig. Im $f=\{f(x)\in G'|x\in G\}$ [全射なら Im$f=G'$] 定理: Ker $f\trianglelefteq G$ Im $f ≤ G'$ 証明: $f(a^{-1}b)=f(a^{-1})f(b)=f(a)^{-1}f(b)=e'^{-1}e'=e'e'=e'$ よって$a^{-1}b\in \text{Ker}\ f$であり、Ker $f$は$G$の部分群である。 $f(xax^{-1})=f(x)f(a)f(x)^{-1}=f(x)f(x)=e'$ よって、xax^{-1}\in \text{Ker}\ fである。Ker$f$は$G$の正規部分群 [準同型写像の定義と性質; $f(a)$はKer $f'$の元] ${}^\forall f(a), f(b)\in \text{Im}\ f$ $f(a)^{-1}f(b)=f(a^{-1}b)\in\text{Im}\ f$ よって Im $f$は$G'$の部分群$...\Box$ 例: [準同型写像] $f:\ \mathbb{C}^*\longrightarrow \mathbb{R}>0$ [乗法から乗法へ] \;\;$z\longrightarrow |z|$は全射準同型写像(単射ではない)である。 証明: $f(z_1 z-2)=|z_1 z_2|=|z_1||z_2|=f(z_1)f(z_2)$ [全射は明らか] Krt $f=\mathbb{T}$ [一次元torus; Ker $f$は複素数平面上の距離1の円→$R$上の$e'=1$に写像] $f:\; \mathbb{R}\longrightarrow \mathbb{R}>0$ [和法から乗法] $x\;\longrightarrow \exp(x)$ [同型写像=全単射写像] 証明: $f(x+y)=\exp(x+y)=\exp(x)\exp(y)=f(x)f(y)$ なお、Ker$f$={0} [行き先での単位元(1)になっていること]

8. 準同型写像: injection: 単射 surjective: 全射 =one-to-one Kernel $ Image:

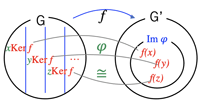
>Top 9. Fundamental homomorphism theorem: 定理: 準同型写像: $f:\ G\longrightarrow G'$を準同型写像という。[Chap 8の定義参照]　 このとき $\varphi: G/\text{Ker}\ f\longrightarrow \text{im}\ f$ $\;\;\;\; x\text{Ker}\ f\longmapsto f(x)$は、同型写像(isomorphism)である。 即ち、$G/\text{Ker}\cong\text{Im}\ f$ 特に、$f$が全射であるときは、$G/\text{Ker}\cong G'$ 但し、$\varphi$が、well-definedであること[定義によって一意の解釈または値が割当荒れること] $\;→x\text{Ker}\ f$の類の別の大表現$y$をとれば、${}^\exists k\in \text{Ker}\ f,\; y=xk$ well=definedの確認: $f(y)=f(xk)=f(x)f(k)=f(x)e'=f(x)$ [$f$は準同型; $f(k)$はKer $f$から取ってきたので$e'$; 即ちwell-definedである。] 証明: $\varphi$が準同型写像であること: $\varphi(x\text{Ker}\ f\; y\text{Ker}\ f)=\varphi(xy\ \text{Ker}\ f)$ $f(xy)=f(x)f(y)=\varphi(x\text{Ker}\ f)\varphi(y\text{Ker}\ f)$ [$\varphi$の定義から] $f(x)\in\text{im}\ f$をとると$\varphi(x\text{Ker}\ f)=f(x)$[全射であることを示す] 証明の準備: $f$が単射⇔$f(x)=e'$ならば$x=e$ $\Rightarrow$は自明 $\Leftarrow$を示す。 $x≠y\in G\;→f(x)≠f(y)\in G'$ $\Rightarrow f(x)=f(y)\in G'\;→x=y\in G$を示す。[対偶] $x,y\in G$に対し、$f(x)=f(y)$とする。 このとき$f(xy^{-1})=f(x)f(y)^{-1}=e’$ 条件より$xy=e$よって$x=y$ [準同型写像なので] $\varphi$が単射であることより、$\varphi(x\text{Ker}\ f)=e'$とする。 [$x\text{Ker}\ f\;→\text{Ker}\ f$であることを示せばよい] $f(x)=e'$となるので、$x\in\text{Ker}\ f$ よって$x\text{Ker}\ f=\text{Ker}\ f$ [xはKer fの中の元なので] 従って、$\varphi$は単射である。$...\Box$ ¶例: ¶$f:\;\mathbb{C}^*\longrightarrow \mathbb{R}>0$ [全射準同型写像] $\qquad\ z\longmapsto |z|$ Ker$\ f=\mathbb{T}\;$[一次元torus $e^{i\theta}$と書ける] →$\mathbb{C}^*/\mathbb{T}\;\cong\mathbb{R}^*$ [$z=re^{i\theta}$を$r$の違いによって分類; 偏角を無視] ¶$f:\;GL_n(\mathbb{R})\longrightarrow \mathbb{R}^*$ [n次一般線形群; 全射準同型写像] $\qquad\ A\longmapsto det\ A$ Ker$\ f=SL_n(\mathbb{R})$ [det=1] →$GL_n(\mathbb{R})/SL_n(\mathbb{R})\cong\mathbb{R}^*$[detの値の違いで分類] ¶ $f:\ S_n\longrightarrow \{-1,1\}$ [全射準同型写像] $\qquad \sigma\longmapsto sgn\ \sigma$ [sgn 偶置換1, 奇置換0] Ker$\ f=A_n\;$ [n次交代群] →$S_n/A_n\ \cong\{-1,1\}$ [偶･偶=偶; 偶･奇=奇と同型] 目的: 準同型写像＝別物に見える群同士が同型であることを示したい →同型写像になる写像の構成手順を教えてくれる。

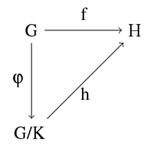
9. 準同型定理: Fundamental homomorphism: (Wiki) 群G,Hおよび群準同型f: G→Hが与えられたとき、Gの正規部分群Kおよび自然な射影φ: G→G/K (剰余群)に対し $K\subset ker(f)$(fの核)が成り立つならば、群準同型 h: G/K→Hが存在して$ f=h\circ φ$とできる。 φはKを単位元に写すG上の準同型の中で最も一般的なもの。 単射矢印:$ \;\hookrightarrow$ 全射矢印:$\;\twoheadrightarrow$ $f: x\in \mathbb{R}\mapsto x^2\in\mathbb{R}_+ $ (非負実数)

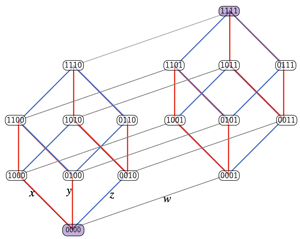
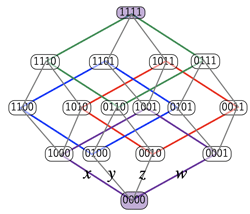
>Top 10. Cf: Partition of Group X: Hasse Diagram: 有限半順序集合(S,≤): Sの元を頂点とし、x<yかつx<z<yとなるzが存在しない場合のみ、 xからyに上向きの線を描く(='yはxを被覆coverする'、または'yはxの直接の後続immediate successorである'という。このような図(=Hasse 図)は半順序を一意的に特定する。		10. Cf: 集合の分割:

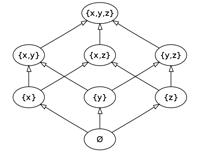
Comment

Group Theory is very abstract; which can expand our thinking more elegant and well organized.

群論は抽象的だが、うまい具合に頭の整理になる。