Processing math: 100%

	Memorandum of Bayes' Theorem	Cat: SCI Pub: 2020 #2013
	Compiled by Kanzo Kobayashi	20726u

Title	Memorandum of Bayes' Theorem	ベイズの定理メモ
Index	Preface: Bayes' theorem: Monty Hall problem: Infection by illnes problem: Defective product ration problem: Secretary problem: Spam mail: HHHHH: IIIII: JJJJJ: KKKKK: LLLLL: MMMMM: NNNN: OOOO: PPPP: QQQQ: RRRR: SSSS:	序文: ベイズ理論: モンティ･ホール問題: 病気感染問題: 製品欠陥率問題: 秘書問題: 迷惑メール: くくくく けけけけ: ここここ: ささささ: しししし: すすすす: せせせせ: そそそそ: たたたた: ちちちち: つつつつ: てててて:
Tag	; ; conditional probabilty; ; ; ; ; insufficient reason; ; ; ; ; ; ;
Why	Reference: Bayesian Statistics The Fun Way by Will Kurt (2020/7) by SB Creative Bayes' Rule with R by James V. Stone (2016) by Sebtel Press Wikipedia, etc.

Original resume

Remarks

>Top 0. Preface: Bayes' theorem describes the probability of an event: discovered Thomas Bayes (1701c-1761) and developed by Pierre-Simon Laplace (1749-1827) This theorem was rediscovered after 200 years, which is a wonderful theorem: the posterior probability as a consequence of two antecedents can be derived from prior probability and a likelihood function. Frequency theory: data is variable, parameter is constant, while Bayes' theorem data is constant, parameter is variable. Bayes' theorem treats probability $p$ of each events which are not independent: conditional probability. Bayes' theorem is effective tool to estimate parameter of a statistical model, or a state-space model; degree of belief is quantified by probability, and when observed data is added, the prior information become posterior information.

0. 序文: Prior

>Top 1. Bayes' theorem Bayesian inference: a method of statistical inference used Bayes' theorem.; which is widely applied in science, engineering, philosophy, medicine, sports, and law. Theorem: $\boxed{P(H|D)=\frac{P(H) P(D|H)}{P(D)}}$ $H$ stands for any hypothesis whose probability is affected by $E$ (=evidence, or data). $P(H)$ is prior probability; estimate of the probability of the hypothesis $H$ before the data $E$. (事前確率: データを見る以前に、自己の仮説の信用率) $D$ is data, or evidence; corresponds to new data that were not used in computing $P(H)$ $P(H|D)$ is the posterior probability; the probability of $H$ given, or after $E$ is observed.; This is what we want to know; the probability of a hypothesis given or after the observed evidence $E$. (事後確率: データを踏まえた上で自己の仮説をどれだけ信じられるか) $P(D|H)$ is the probability of observing $D$ given $H$, and is called the likelihood. As a function of $D$ with $H$ fixed, it indicated the compatibility of the evidence with the given hypothesis. (尤度: 自己の仮説が正しいとした場合に、既存のデータが得られる確率) $P(D)$ is termed marginal likelihood or model evidence; this factor is the same for all possible hypotheses being considered. (仮説に関係なく、このデータが観察される確率。事後確率が0と1の間に収まるようにする。このデータを決めるのは難しい。) $→P(H|D)\propto P(H) P(D|H)$ [事後確率比→事後オッズ] $\frac{P(D\H_1)}{P(D\H_2)}$ (ベイズ因子: 自説を支持する可能性と、他説を支持する可能性との比較) → 自説が指示されるかどうか気にせずに、自説が観測データとどれだけよく支持するかにのみ着目する。→自説を裏付けを得るか、または自説の裏付けが弱くなり自説を変えざるを得なくなるか。) $\boxed{P(H|D)=\frac{P(D|H)P(H)}{P(D|H)P(H)+P(D|\lnot H)P(\lnot H)}}$ where, $P(H)+P(\lnot H)=1$, and $P(D)=P(D|H)P(H)+P(D|\lnot H)P(\lnot H)$ Rule of multiplication: $P(D\cap H)=P(D|H)P(H)=P(H|D)P(D)$

1. ベイズ理論: given that: もしthat以下ならば likelihood: 尤度 maximum likelihood estimate: 最尤推定 sample space: 標本空間 probability space: 確率空間 elementary event: 根元事象 Bayesian inference: ベイズ推定 prior probability: 事前確率 =conditional potability: 条件付き確率 probability of A given B: $P(A|B),\;P_B(A)$ likelihood function: 尤度関数 marginal likelihood: 周辺尤度 posterior probability: 事後確率 uniform distribution: 一様分布 ベイズ理論: Flip causation: 因果関係を逆転 Prior P: $P(\theta)$ Posterior P: $P(\theta|X)$ $P(\theta|X) =P(\theta)･\frac{P(X|\theta)}{P(X)}$ EAP (Expected a posteriori): $=\int f(\theta|X)\theta d\theta$ $=\int \frac{f(X|\theta)f(\theta)} {f(X)}\theta d\theta$ Bayes Theorem: Probability of Hypothesis given the Evidence equals Likelihood of Evidence ☓ Prior Probability in all positives (True or False)

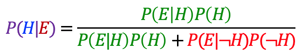
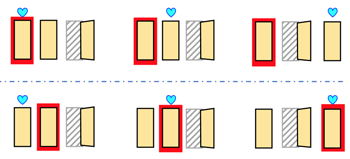
>Top 2. Monty Hall problem: By US TV game show 'Let's Make a Deal' after its original host, Monty Hall. Suppose you're on a game show, and you're given the choice of three doors. Behind the one door is a present; behind others nothing. You pick a door, say #1, and the host, who knows what's behind the doors, opens another door which has nothing. He then says to you, "Do you want to pick the door #2?" Is it to your advantage to switch your choice? Under the standard assumptions, contestants who switch have a $\frac{2}{3}$ chance of winning a present, while contestants who stick to their initial choice have only a $\frac{1}{3}$ chance. ¶Let the event of three doors as $A, B, C$ having a possible present behind, and the event by opening a door by the host as $a, b, c$: then, the probability of regarding the door $A$ when the host opened the door $c$. $P_c(A)=\frac{P(A)P_A(c)}{P(c)}=\frac{\frac{1}{3}\frac{1}{2}}{P(c)}$ $P_c(B)=\frac{P(B)P_B(c)}{P(c)}=\frac{\frac{1}{3}･1}{P(c)}$ $→2P_c(A)=P_c(B),\;P_c(A)+P_c(B)=1$ $\therefore\;P_c(A)=\frac{1}{3},\;P_c(B)=\frac{2}{3}$ → The advantage is to switch your choice. 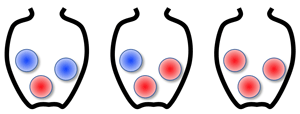¶Here are three vases $A, B, C$ containing 2 blue balls & 1 red ball, 1 blue ball & 2 red balls, and 3 red balls respectively. Pick up 1 ball from each vase, which was a red ball. Find probability such that the red ball was taken from the vase containing 3 red balls. $H_1: picked up 1 ball from the vase A containing 1 red ball$ $H_2: picked up 1 ball from the vase A containing 2 red ball$a $H_3: picked up 1 ball from the vase A containing 3 red ball$a $D: 1 ball picked up was red$ $P_0(H_3)=\frac{P(H_3)P_{H_3}(D)} {P(H_1)P_{H_1}(D)+P(H_2)P_{H_2}(D)+P(H_3)P_{H_3}(D)}$...(*) >Top Probability is considered as same unless any information: [Principle of insufficient reason] here: $P(H_1)=P(H_2)=P(H_3)=\frac{1}{3}$ (*): $$P_0(H_3)=\frac{\frac{1}{3}･\frac{3}{3}} {\frac{1}{3}･\frac{1}{3}+\frac{1}{3}･\frac{2}{3}+\frac{1}{3}･\frac{3}{3}} =\frac{1}{2}$ This problem is applicable to other cases, such that; spam mail filter uses vases as mail or documents, and balls as words.

2. モンティ･ホール問題: 壺とボールの問題:

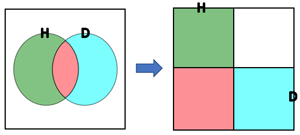
>Top 3. Infection by illness problem: Infection by illness: Probability of who are sick: $P(B_1)=0.0001$ Probability of who are not sick: $P(B_2)=0.9999$ Probability of showing positive who are sick: $P(A|B_1)=0.95$ [true positive] Probability of showing positive who are not sick: $P(A|B_2)=0.20$ [false positive] Then, probability of being sick who are positive: $P(B_1|A)$ $=\frac{P(B_1)P(A|B_1)}{P(B_1)P(A|B_1)+P(B_2)P(A|B_2)}$ $=\frac{0.0001･0.95}{0.0001･0.95+0.9999･0.20}=0.000475$

3. 病気感染問題:

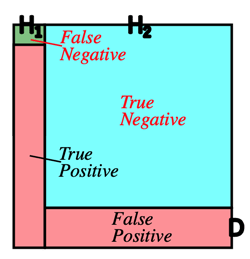
¶Medical diagnosis: Medical care indicates that different illnesses may produce identical symptom. Suppos a particular set os symptoms, denoted as even $H$, occurs infected any one of three illness - $A, B, C$. (for simplicity, $A, B, C$ are mutually exclusive). Studies show these probabilities of getting the three illnesses: $P(A)=.01; P(B)=.005; P(C)=.02$ The probabilities of developping the symptoms $H$, given a spcific illness, are: $P(H|A)=.90; P(H|B)=.95; P(H|C)=.75$ Assuming that an ill person shows the sysmptoms $H$, what is the probability that the person has illness $A$? $P(A|H)=\frac{P(A)P(H|A)}{P(A)P(H|A)+P(B)P(H|B)+P(C)P(H|C)}$ $=\frac{.01\times .90}{.01\times .90+.005\times .96+.02\times .75}=.3130$

Say: A: Covid-19 B: Pneumonia C: Influenza H: fever

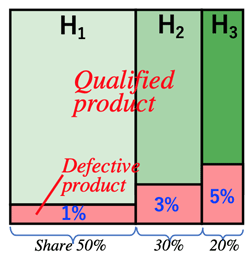
>Top 4. Defective product ratio problem: Defective product ratio: A certain product is made in three factories $A, B, C$, have its share 50%, 30%, 20% respectively; and its ratio of defective product is 1%, 3%, 5% respectively. ¶When some defective product is claimed, find the probability which factory-C made it. Product share of $A$: P(B_a)=0.5 Product share of $B$: P(B_b)=0.3 Product share of $C$: P(B_c)=0.2 Defective product ratio of $A$: P(A|B_a)=0.01 Defective product ratio of $B$: P(A|B_b)=0.03 Defective product ratio of $C$: P(A|B_c)=0.05 Then the ratio of defective product made in factory-C: P(B_c|A) $=\frac{P(B_c)P(A|B_c)}{P(B_a)P(A|B_a)+P(B_b)P(A|B_b)+P(B_c)P(A|B_c)}$ $=\frac{0.2･0.05}{0.5･0.01+0.3･0.03+0.2･0.05}=0.4177$

4. 製品欠陥率問題:

>Top 5. Secretary problem: Also known as marriage problem, or best choice problem. Formulation: There is a single position to fill. There are $n$ applicants for the position, and the value of $n$ is known. The applicants are interviewed sequentially in random order. After an interview, the interviewed applicant is either accepted or rejected immediately, which is irrevocable. The decision can be based only on the relative ranks of the applicants interviewed so far. The objective is to have the highest probability of selecting the best applicant of the whole group. Proof: Let the No.1 exists in $k$-th in total $n$ applicants. The interviewer rejects unconditionally the first $t$ applicants in total $n$ applicants. The condition of selecting No.1 is: there is tentatively best applicant within the range of until $t$-th applicant until $(k-1)$-th applicants . The probability is selecting $t$ within $k-1$: that is $\frac{t}{k-1}$ if $t≥k$ the probability is $0$, and if $t<k$ is $\frac{t}{k-1}$. the probability of No.1 exists $k$-th is $\frac{1}{n}$ thus: Probability of selecting the best applicant: $P(t)=\frac{1}{n}\displaystyle\sum_{k=t+1}^n\frac{t}{k-1} =\frac{t}{n}\big(\frac{1}{t}+\frac{1}{t+1}+\cdots+\frac{1}{n-1}\big)$...(*) The answer is the maximum $t$ of (*) here: $\big(\frac{1}{t}+\frac{1}{t+1}+\cdots+\frac{1}{n-1}\big)\simeq \ln\frac{n}{t}$ thus: $\frac{1}{n}\displaystyle\sum_{k=t+1}^n\frac{t}{k-1} =\frac{t}{n}\ln\frac{n}{t}$ $\big(\frac{t}{n}\ln\frac{n}{t}\big)'=\frac{1}{n}\ln\frac{n}{t}-\frac{1}{n}$...(**) find max $t:\;\ln\frac{n}{t}=1\;→\frac{n}{t}=e\;→\therefore\;t=\frac{n}{e}$ Cf: when $n=100$, then $t=\frac{100}{3}=36.765\simeq=37$ $P(t)=\frac{t}{n}\ln\frac{n}{t}=\frac{37}{100}\ln e=0.37$

5. 秘書問題: from Maclaurin's extension: $e^x=\displaystyle\sum_{k=0} ^{\infty}\frac{x^k}{k!} -1+x+\frac{x^2}{2} +\frac{x^3}{6}+\cdots$ $→e^x≥1+x$ then: $\exp(1+\frac{1}{2}+\frac{1}{3} +\cdots+\frac{1}{n}$ $=\exp(1)\exp(\frac{1}{2}) \cdots\exp(\frac{1}{ｎ})$ $≥(1+1)(1+\frac{1}{2})\cdots (1+\frac{1}{n})$ $=2\frac{3}{2}\frac{4}{3}\cdots \frac{n+1}{n}=n+1$ $→\displaystyle\sum_{k=1}^n ≥\ln(n+1)$　 Euler constant: $\gamma$ $=\displaystyle\lim_{n\to\infty} (\displaystyle\sum_{k=1}^n \frac{1}{k}-\ln n)$ Secretary problem:

>Top 6. Spam mail: $\cases{\text{Spam mail}=A_1\\\text{Not-Spam mail}=A_2}$ generally 70% is smal mail: $P(A_1)=0.7$ when mail B contains the word of for free: $P(B|A_1)=0.09,\;P(B|A_2)=0.01$ then: $P(A_1|B)=\frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)}$ $=\frac{0.09\times 0.7}{0.09\times 0.7+0.01\times(1-0.7)}\approx 0.9545$ when the mail contains sure victory: $P(C|A_1)=0.11,\;P(C|A_2)=0.02$ then: $\frac{0.11\times 0.9545}{0.11\times 0.9545+0.02\times(1-0.9545)}\approx 0.9914$ further, when the mail contains definite answer: $P(D|A_1)=0.14,\;P(C|A_2)=0.03$ then: $\frac{0.14\times 0.9914}{0.14\times 0.9914+0.03\times(1-0.9914)}\approx 0.9981$ furthermore, when the mail contains bonus: $P(D|A_1)=0.07,\;P(C|A_2)=0.01$ then: $\frac{0.07\times 0.9981}{0.07\times 0.9981+0.01\times(1-0.9981)}\approx 0.9997$

6. 迷惑メール:

>Top ７. xxxx:

7. xxxx:

>Top ８. xxxx:

8. xxxx:

>Top 9. xxxx:

9. xxxx:

>Top 10. xxxx:

10. xxxx:

>Top 11. xxxx:

11. xxxx:

>Top 12. xxxx:

12. xxxx:

>Top 13. xxxx:

13. xxxx:

>Top 14. xxxx:

14. xxxx:

>Top 15. xxxx:

15. xxxx:

>Top 16. xxxx:

16. xxxx:

>Top 17. xxxx:

17. xxxx:

>Top 18. xxxx:

18. xxxx:

>Top 19. xxxx:

19. xxxx:

>Top 20. xxxx:

20. xxxx:

>Top 21. xxxx:

21. xxxx:

>Top 22. xxxx:

22. xxxx:

>Top 23. xxxx:

23. xxxx:

>Top 24. xxxx:

24. xxxx:

>Top 25. xxxx:

25. xxxx:

Comment

a

a