N(μ,σ2)
Memorandum of Probablity Statistics
Cat: SCI
Pub: 2020
#2012a
Compiled by Kanzo Kobayashi
20726u
Title
Memorandum of Probality Statistics
確率統計学メモ
Index
- Preface:
- Basic knowledge:
- Moment-generating function:
- Normal distribution:
- Binomial distribution:
- Beta distribution:
- Poisson distribution:
- Geometric distribution:
- Exponential distribution:
- Hypergeometric distribution:
- Cauchy distribution:
- Markov chain:
- Infinite series:
- Least squares method:
- xxxx:
- xxxx:
- xxxx:
- xxxx:
- xxxx:
Tag
; ; ; ; ; ; ; ; ; ; ; ; ; ;
Why
-
Original resume
Remarks
>Top 0. Preface:
- In with the Covid-19 age, we need to be more conscious of risk management or uncertainty by using probability statistics.
- Probability statistics is a useful knowledge how to understand events or the real world through hypothesis and its verification, and through purposive mathematics.
- Descriptive statistics clarifies structure of the object, and inferential statistics estimated the total by partial sampling, and multivariate analysis describes correlationship among various elements.
- Statistics can estimate the total by its part, conversely which estimates the part by its total.
- Even big data is a big sample, which is collected to clarify correlationship of elements, and is used to make effective decision making.
- Statistical software R is very effective in understanding behavior of probability statistics, which looks like a trigonometric table or logarithmic table before computer age.
1. 序文
- コロナウイルス時代のリスク計算
- 記述統計学と推計統計学
- ビッグデータ=大きなサンプル
→各要素間の相関関係が重要
- 統計ソフトウェアR
>Top 1. Basic knowledge:
- Permutation: nPr=n!(n−r)!
- Combination: nPrrPr=n!(n−r)!r!
- Permutation (with same events): nPn=n!p!q!⋯s!
- Circular Permutation:n−1Pn−1=(n−1)!
- Repeated Permutation:nΠr=nr
- 8 digits of binary: 28=256
- consider 0 group?; different group?
- Repeated Combination (Homogeneous product): nHr=n+r−1Cn−1=n+r−1Cr
- divide 2 groups from different kind of n: 2n−22=2n−1−1
- Pascal's theorem: nCr=n−1Cr+n−1Cr−1
- Binomial theorem: (a+b)n=n∑r=0nCran−rbr
=nC0an+nC1an−1b+⋯+nCnbn
- Conditional probability: P(B|A)=P(A∩B)P(A)
- Law of multiplication: P(A∩B)=P(A)P(B|A)=P(B)P(A|B)
- Bayes' theorem:
- P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+⋯+P(Ar)P(B|Ar)
- P(Ai|B)=P(B∩Ai)P(B)=P(Ai)P(B|Ai)P(B),[i=1,2,⋯,r]
- where: A1∪A2∪⋯∪Ar=Ω
- Expectation value lineality:
- Expectation value: X→Y=aX+b [lineality]
E(aX+b)=∑i(axi+b)Pi=a∑ixiPi+b∑iPi
=aE(X)+b
- continuous function: E(X)=∫∞−∞xp(x)dx
E(aX+b)=∫∞−∞(ax+b)P(X)dx=a∫xP(X)dx+b∫P(x)dx=aE(X)+b
- Expectation value: E[X]=n∑i=1pixi
- E[aX]=aE[X] [Linearity]
- E[X+a]=E[X]+a
- E[X+Y]=E[X]+E[Y]
- E[XY]=E[X]E[Y],(X,Y; uncorrelated)
- Variance: V[X]=E[(X−μ)2]=n∑i=1Pi(xi−μ)2
- V[X]=∑i(xi−μ)2Pi
=∑(x2iPi−2μxiPi+μ2Pi)=x2iPi−∑2μxiPi+∑μ2Pi
=E[X2]−2μE(X)+μ2=E[X]2−μ2=E(X2)−(E(X))2
- V[aX]=a2V[X]
- V[X+a]=V[X] [parallel translation]
- V[X+Y]=V[X]+V[Y],(X,Y; uncorrelated)
- Covariance: Cov(X,Y)=E[(X−μX)(Y−μY)]=E[XY]−μXμY
Cov(X,Y)=E[XY−XμY−YμX+μXμY]
=E[XY]−E[XμY]−E[YμX]+E[μXμY]
=E[XY]−μXμY−μXμY+μXμY
- Correlation coefficient: ρ=Cov(X,Y)σXσY
- ρ∼1 strongly correlated; ρ∼−1 reversely correlated
- Cov(X,Y)=E[XY]−E[X]E[Y]
- V[X+Y]=V[X]+V[Y]+2Cov(X,Y)
- Chebyshev's inequality:
- when: E[X]=μ,andV[X]=σ2 are known,
a>0→P[|X−μ|≥aσ]≤1a2
- Markov's inequality:
- P[X≥c]≤E[X]c,[c>0,X:probability variable]
- Proof: E[X]=∫∞0xfX(x)dx
=∫c0xfX(x)dx+∫∞cxfX(x)dx
≥∫∞cxfX(x)dx≥c∫∞cfX(x)dx
=cP[X≥c]
- Proof:
substitute to Markov's inequality: X=(Y−μ)2,c=a2σ2
P[(Y−μ)2]≥a2σ2≤E[(Y−μ)2]a2σ2
→P[|Y−μ|≥aσ]≤1a2
- ¶ when: c=a2→P[|X−μ|≥a]≤σ2a2→0,(n→+∞)
[law of large numbers]
2. 基礎知識:
- sample space:Ω 標本空間
- probability space: 確率空間
- expectationv value: 期待値
- stochastic variable: 確率変数
- empty set:∅
- sum set:∪ 和集合
- product set:∩ 積集合
- complementary set: 余集合
- law of large numbers: 大数の法則
- conditional probability: 条件付確率
- law of multiplication: 乗法法則
- covariance: 共分散
- correlation coefficient: 相関係数
- unbiased variance: 不偏分散
- law of large numbers: 大数の法則
- 105=100,000
- 10!=3,628,800
>Top 2. Moment-generating function:
- Moment-generating function:
- MX(t)=E(etX)=∑ietxif(xi)
- M′X(t)|t=0=E(X)
- M″X(t)|t=0=E(X2)
- M(k)X(t)|t=0=E(Xk)
- here: ∑ietxi=∑i(1+txi1!+(txi)22!+⋯)f(Xi)
→E(X)+tE(X2)+⋯+
- ¶P(X=k)=nCkpkqn−k,(k=0,1,2,⋯,n)
MX(t)=n∑k=0etknCkpkqn−k=n∑k=0nCk(pet)kqn−k=(q+pet)n
- M′X(t)=npet(q+pet)n−1
- →E(X)=M′X(t)|t=0=np
- M″X(t)=npet(q+pet)n−1+npet(n−1)(q+pet)n−2pet
=npet(q+pet)n−2(q+npet)
- →E(X2)=M″X(t)|t=0=np(q+np)=npq+(np)2
→V(X)=E(X2)−E(X)2=npq
- Tossing coins:
- ¶Toss 5 coins simultaneously: got 2 heads and 3 tails.
- Ω: pick up 5 coins out of 2 cases (head or tail) repeatedly:
2Π5=25=32
- P(A): 2 heads out of 5 trials: 5C2=10
- Playing cards: 4 kinds ☓ each 13 cards=52 cards
- ¶pick up 3 different mark cards out of 52 playing cards without joker.
- Ω:pickup3cardsoutof52:52C3=22100
- Pick up 3 kind cards out of 4 kinds: 4C3=4
- Picking up each kind of a card out of 13 cards of each kind: 13Π3=2197
- P(A):=4・2197/22100=0.3976:
2. 積率母関数:
- binomial distribution: 二項分布
- moment-generationg function: 積率母関数
- geometric distribution: 幾何分布
- Geometric distribution:
The probability distribution of the number of 1) failures before the first success or 2) Bernoulli trials needed to get first success.
>Top 3. Normal Distribution (ND):
- Definition: X∼N(μ,σ2)
- N(μ,σ2):
f(x)=1σ√2πe−12(x−μσ)2=1√2πσexp(−(x−μ)22σ2)
- SND: N(0,1):ϕ(x)=1√2πe−x22
- Sample average: ˉX=X1+⋯+Xnn
- Sample variance: X2=(X1−ˉX)2+⋯+(Xn−ˉX)2n
- E[S2]=σ2−1nσ2=n−1nσ2
- Unbiased sample variance: U2=(X1−ˉX)2+⋯+(Xn−ˉX)2n−1
- E[U2]=σ2
- Interval estimation:
- ¶Estimate μ at 95% reliability in a population: μ=?,assume:σ2=6
- take a sample of X from the population:
μ−1.96σ≤X≤μ+1.95σ, [95% probability]
→X−1.96σ≤μ≤X+1.96σ
where, σ=6,X=165→153.24≤μ≤176.76
[95% reliability]
- →95% of interval of reliability includes the population mean.
- ¶take sample: X1,⋯,Xn
ˉX follows a SD with average μ, and variance μ2n
- ¶take 9 samples: N=9; (165, 170, 163, 171, 161 162 180, 158, 164); then estimate μ with 95% reliability.
μ−1.96σ√n≤ˉX≤μ+1.96σ√n
→ˉX−1.96σ√n≤μ≤ˉX+1.96σ√n
here:
σ√n=2,ˉX=166
→162.62≤μ≤169.92
- Generally, in a SD, reliable interval with reliability α is:
ˉX−kω√n≤μ≤ˉX+kω√n,[k:100(1−α)]point of both sides of a SD.
- SND (μ=0,σ2=1)
when α=0.95
5% points [100(1-0.95)=5]...1.96σ=1.96
- Stochastic variable X:
- P(a≤X≤b)=∫baf(x)dx [probability density function]
- f(x)=1√2πσe−(x−μ)22σ2 [ND]
- when: X=Bin(n,p)=nCkpk(1−p)n−k
→X−np√np(1−p)[SD;E[X]=np,σ2=np(1−p)]
- Standardization of probability degree: μ=0,σ2=1
- E[aZ+b]=aE[X]+b
V[aX+b]=a2V[X]
- V[X]=E[(X−E[X])2]=E[X2]−E[X]2
- ¶Data of SD <-(1,2,3,4,5,6,7,8,9,10)
- E[X]=μ=1nn∑i=1xi=5.5
- V[X]=σ2=1nn∑i=1(xi−μ)=E[X2]−μ2=38.5−30.25=8.25
- σ≈2.87
3. 正規分布:
- Normal distribution, Gaussian distribution: 正規分布
N(μ,σ2)
- Standard ND: 標準正規分布N(0,1)
- (parent) population: 母集団
- point estimation: 点推定
- sample mean: 標本平均
- unbiased variance: 不偏分散
- estimator: 推定量ˆθ
- interval estimation: 区間推定
- degree of reliability: 信頼度
- stochastic variable: 確率変数
- t-distribution: t分布
- N(μ,σ2)
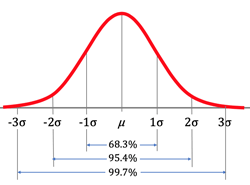
from μ
Rareness
σ
every 3 days
2σ
3 weeks
3σ
1 year
4σ
40 years
5σ
5,000 years
6σ
1.4 million years
>Top 4. Binomial distribution:
- Binomial distibution is a discrete probability distribution of the number of success in a sequnece of n independent experiments. (=Bernoulli trial)
- Definition:
- Bi(k;n,p)(0≤p≤1,q=1−p)
P(X=k)=nCkpkqn−k,(k=0,1,2,⋯,n)
- n∑k=0nCkPkqn−k=(q+p)n=1
- E(X)=n∑k=0knCkPkqnk
=n∑k=1kn!(n−k)!k!pkqn−k
=npn∑k=1(n−1)!(n−k)!(k−1)!pk−1qn−k=np
- V(X)=E(X2)−E(X)2=E(X(X−1))+E(X)−E(X)2
- E(X(X−1))=n∑k=2k(k−1)n!(n−k)!k!pkqn−k
=n(n−1)p2n∑k=2n−2Ck−2pk−2qn−k
=n(n−1)p2(q+p)n−2=n2p2−np2
- ∴
- ¶Winning ticket: p=120/1000, when we buy n=10 lottery tickets
- P(X=k)={}_nC_kp^k(1-p)^{n-k}
- then P(X=0)={}_10C_0・0.12^0(1-0.12)^{10-0}=0.279
P(X=1)=0.380,\; P(X=2)=0.233
4. 二項分布:
- Bernoulli trial: ベルヌーイ試行
- Bi(k;n,p): n,p→k
- probability p of getting k successes in n independent trials.
- P(k;n,p)=\binom{n}{k}p^kq^{n-k}
- E[X]=np
- V[X]=npq
- p«1, n»1大→Poisson分布
- !=choose (n,k)
- PDF (Probability Density Function)
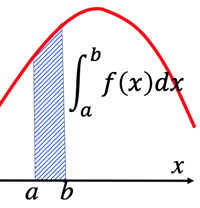
>Top 5. Beta distribution:
- Beta distribution is similar to Binomial distribution, but those behaviors are quite different; Beta distribution aims to calculate prausible probability of assumed probabilty
- Beta distribution (first kind): a continuous probability distribution on the interval [0,1], denoted by \alpha and \beta as exponents of the random variable:
- In Bayesian inference, this is the conjugate prior probability distribution for the Bernoulli, binomial, negative binomial, and geometric distributions, and is a suitable model for the random behavior of percentages.
- f(k;n,p): (k,n) known→p unknown
p=probability of a certain event, \alpha=number of interesting events happened, \beta=numbr of interesting events not happened.
here: beta function is an adjustment to make the total of probability=1
- f(x)=Cx^{\alpha-1}(1-x)^{\beta-1}
- \boxed{\text{Beta} (p;\alpha,\beta)=\frac{p^{\alpha-1}(1-p)^{\beta-1}}{\text{beta}(\alpha,\beta)},
\;[0≤x≤1,\; \alpha,\beta>0]}
- E[X]=\frac{\alpha}{\alpha+\beta}
- V[X]=\frac{\alpha\beta}{(\alpha+\beta)^2(\alpha+\beta+1)}
- ¶tossing a coin: 4 head and 6 tails in 10 trials. Calculate p≥60%:
- Using R funtion:
>integrate(function(x) dbeta(x,4,6, 0.60, 1)
=1.1e-15\approx10%
- R:
5. ベータ分布:
- Probability density function: 確率密度関数
- conjugate prior probability distribution: 共役事前分布×ある尤度=事後分布と同じ分布
- conversion: proportion of people viewing AD and going or click to buy the product.
- Beta distribution (PDF)
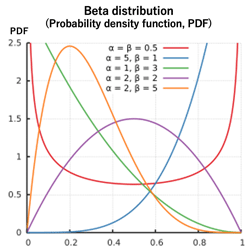
>Top 6. Poisson distribution:
- A discrete probability distribution which expresses the probability of random events occurring in given number of times (k) times in a certain unit time, if these events randomly occur with mean rate of the times (\lambda) since the last event.
- X~P_0(\lambda)
- \boxed{P(k)=e^{-\lambda}\frac{\lambda^k}{k!}}
- Repeated trial: {}_nC_kp^{k}(1-p)^{n-k}
- Poisson distribution approaches to Normal distribution as the increase of \lambda.
- ¶ratio of defective product: \frac{1}{200} The probability of defective ratio of 10 products:
- \lambda=np=10・\frac{1}{200}=0.05
P(1)=\frac{e^{-\lambda}\lambda^k}{k!}=\frac{e^{0.05}・0.05^1}{1!}=0.048
- ¶Lottery: winning ratio p=0.002; buying n=200 tickets
- E(x)=\lambda=np=0.4
- winning ration of buying k=1 ticket is:
P(X=1)=\frac{e^{-\lambda}\lambda^k}{k!}
=\frac{e^{-0.4}0.4^1}{1!}=0.2681
- Bi(200,1)={}_nC_kp^k(1-p)^{n-k}=
{}_200C_1・0.002^1・(1-0.002)^{200-1}=0.2686
6. ポアソン分布:
- P_{\lambda}(k)=e^{-\lambda}
\frac{\lambda^k}{k!}
- E(X)=\lambda
- V(X)=\lambda
- Poisson distribution can be calcultaed by \lambda only, without knowing n, p.
>Top 7. Geometric distribution:
- Assumption:
- independent trials
- only two possible outcomes for each trial
- possibility P(X) is same for every trial
- Definition: number of Bernoulli trials (success or failure)
- case: number of failures:
X~Geo(P): \boxed{P(X=k)=pq^k,\;(k=0,1,2,\cdots)}
→\displaystyle\sum_{k=0}^{\infty}pq^k=p\frac{1}{1-q}=1
- M_X(t)=E(e^{tX})=\displaystyle\sum_{k=0}^{\infty}e^{tk}pq^k
=p\displaystyle\sum_{k=0}^{\infty}(e^tq)^k=\frac{p}{1-e^tq}
- M_X'(t)=-p(1-e^tq)^{-2}(-e^tq)=pqe^t(1-e^tq)^{-2}
- M_X''(t)=pqe^t(1-e^tq)^{-2}-pq^2e^{2t}(-2)(1-e^tq)^{-3}
- E(X)=M_X'(0)=pq\frac{1}{p^2}=\frac{q}{p}
- E(X^2)=M_X''(0)=\frac{q}{p}+2\frac{pq^2}{p^3}
=\frac{q}{p}+2(\frac{q}{p})^2
- V(X)=E(X^2)-E(X)^2=\frac{q}{p}(1+\frac{q}{p})=\frac{q}{p^2}
- or case of first success: X→X+1 of the above:
P(X=k)=p(1-p)^{k-1}
- E(X+1)=E(X)+1=\frac{1}{p}
- V(X+1)=V(X)=\frac{q}{p^2}
7. 幾何分布:
- Geometric distribution: 幾何分布
- Bernoulli trials: ベルヌーイ試行
- case of first success:
- P(X=k)=p(1-p)^{k-1}
- E(X)=\frac{1}{p}
- V(X)=\frac{1-p}{p^2}=\frac{q}{p^2}
>Top 8. Exponential distribution:
- Feature:
- Probability distribution of the time between events in a Poisson distribution
- a continous analogue of Geometric distribution
- key property of being memoryless
- f(X;\lambda)=\lambda e^{-\lambda x},\; [\lambda: rate parameter]
- E(X)=\frac{1}{\lambda}
- V(X)=\frac{1}{\lambda^2}
- M_X(t)=\frac{\lambda}{\lambda-t}
- Proof:
- E(X)=\displaystyle\int_0^{\infty}xf(x)dx
=\displaystyle\int_0^{\infty}x\lambda e^{-\lambda x}dx
=\lambda\displaystyle\int_0^{\infty}x(-\frac{1}{\lambda}e^{-\lambda x})'dx
=\displaystyle\lambda\big(\big[x(-\frac{1}{\lambda}e^{-\lambda x}\big]_0^{\infty}
-\int_0^{\infty}-\frac{1}{\lambda}e^{-\lambda x}dx\big)
=\frac{1}{\lambda}
- E(X^2)=\displaystyle\int_0^{\infty}x^2f(x)dx
=\displaystyle\int_0^{\infty}x^2\lambda e^{-\lambda x}dx
=\frac{2}{\lambda^2}
- V(X)=E(X^2)-E(X)^2=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}
=\frac{1}{\lambda^2}
- or each random event occurs per time \mu
f(X)=\frac{1}{\mu}e^{-\frac{x}{\mu}},\; (x≥0)a
- E[X]=\displaystyle\int_0^{\infty}xf(x)dx=\mu
- V[X]=\mu^2
8. 指数分布:
- memorylessness: 無記憶性
>Top 9. Hypergeometric disribution:
- Definition:
- Population of size N contains K successful objects; k successed in n total draws with replacement.
- P(X=k)=\frac{\binom{K}{k}\binom{N-K}{n-k}}{\binom{N}{n}}
=\frac{\binom{n}{k}\binom{N-n}{K-k}}{\binom{N}{K}}
- E(X)=\frac{nK}{N}
- ¶K=10 red balls and 20 white balls, total N=30 balls in a vase. Pick up n=5 balls and find the probability of just k=1 red ball is selected.
- \frac{\binom{10}{1}\binom{30-10}{5-1}}{\binom{30}{5}}
=\frac{8075}{23751}\approx 0.34
9. 超幾何分布:
- Discrete probability distributon describes the probability of k success in n draws without replacement.
- Cf: Binominal distibution describes the probability of k in n draws with replacement.
>Top 10. Cauchy distribution:
- Case: Outliner is a data which differs significalty from other data, and sometimes has an important meaning. An outliner can cause serious problems in statistical analyses.
In samplings of data, some data points will be further away from the mean than what is deemed reasonable. (due to systematic error, erroneous procedure, or theory is not valid; anomaly; e.g. average temperature in a room, if sampled it on the oven)
- Defintion:
- f_X(x)=\frac{1}{\pi(1+x^2)}
- E(X)=\mu=\frac{1}{\pi}\displaystyle\int_{-\infty}^{\infty}\frac{x}{1+x^2}dx
=\frac{1}{\pi}\displaystyle\int_0^{\infty}\frac{x}{1+x^2}dx
+\frac{1}{\pi}\displaystyle\int_{-\infty}^0\frac{x}{1+x^2}dx=\infty-\infty
[not defined]
- \displaystyle\int_a^b\frac{x}{1+x^2}dx
=\frac{1}{2}\ln(1+b^2)-\frac{1}{2}(1+a^2),\;(a→-\infty,\;b→\infty)
- V(X)=\frac{1}{\pi}\displaystyle\int_{-\infty}^{\infty}\frac{x^2}{1+x^2}dx
[not defined]
10. コーシー分布:
- outliner: 外れ値
- skewness: 非対称
- 異常値、想定外
- 証券暴落、バブル崩壊、Pandemic virus
- 大数の法則、中心極限定理、期待値、分散存在せず。
- Bell curve vs. Cauchy curve:
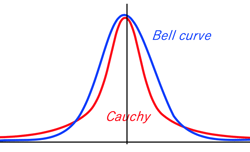
>Top 11. Markov chain:
- Probability of each event depends only on the previous state; future outcomes based solely on its present state, its future and past states are independent.
- Definition:
- P(X_{t+1}|X_t,X_{t-1},\cdots,X_1)=P(|X_{t+1}|X_t)
- Transition probability: P(X_{t+1}|X_t)
- ¶P=\pmatrix{P11&P12&P13\\P21&P22&P23\\P31&P32&P33}
=\pmatrix{0.7&0.3&0\\0.4&0.4&0.2\\0.3&0.3&0.4}
- →P^2=\pmatrix{0.61&0.33&0.06\\0.5&0.34&0.16\\0.45&0.33&0.22}
11. マルコフ連鎖:
- transition probability: 遷移確率
- 晴曇: 今日晴れ→明日曇りの確率
- \pmatrix{晴晴&晴曇&晴雨
\\曇晴&曇曇&曇雨
\\雨晴&雨曇&雨雨}
- 0≤各確率≤1, 行和=1
- 2日後の天気: P^2
>Top 12. Infinite series:
- Harmonic series:
- 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots
=\displaystyle\sum_{k=1}^n\frac{1}{k}=\infty
- Proof:
- 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\cdots
>1+\frac{1}{2}+\big(\frac{1}{4}+\frac{1}{4}\big)+
\big(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\big)+\cdots
=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots
- \displaystyle\sum_{k=1}^{2^p}≥1+\frac{p}{2}
when p→\infty then, the right side→\infty
- Maclaurin expansion:e^x=\displaystyle\sum_{k=o}^{\infty}
\frac{x^k}{k!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots
- Proof:
- \exp(1+\frac{1}{2}+\frac{1}{2}+\cdots+\frac{1}{n})
=\exp(1)\exp(\frac{1}{2})\exp(\frac{1}{3})\cdots\exp(\frac{1}{n})
≥(1+1)(1+\frac{1}{2})(1+\frac{1}{3})\cdots(1+\frac{1}{n})
=2\frac{3}{2}\frac{4}{3}\cdots\frac{n+1}{n}=n+1
- →\displaystyle\sum_{k=1}^n\frac{1}{k}≥\ln(n+1)
when n→\infty then, the right side→\infty
- Mercator series:
- 1-x+x^2-x^3+x^4-\cdots+(-1^x)^{n-1}
- 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots
=\displaystyle\sum_{k=1}^{\infty}\frac{(-1)^{k-1}}{k}=\ln 2
- here: n=2: 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}
=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4})-2(\frac{1}{2}+\frac{1}{4})
=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4})-(1+\frac{1}{2})
=\frac{1}{3}+\frac{1}{4}
- \displaystyle\sum_{k=1}^{2n}\frac{(-1)^{k-1}}{k}
=\big(\sum_{k=1}^{2n}\frac{(-1)^
{k-1}}{k}+2\sum_{k=1}^n\frac{1}{2k}\big)
-2\sum_{k=1}^n\frac{1}{2k}
\displaystyle\sum_{k=1}^{2n}\frac{1}{k}-\sum_{k=1}^n\frac{1}{k}
=\sum_{k=1}^n\frac{1}{n+k}
- \displaystyle\lim_{n\to\infty}\sum_{k=1}^n\frac{1}{n+k}
=\lim_{n\to\infty}\sum_{k=1}^n\frac{1}{1+\frac{k}{n}}
=\displaystyle\int_0^{1}\frac{1}{1+x}dx=\ln 2
- a
12. 無限級数:
- initial value: 初項
- common ratio: 公比
- alternating series: 交代級数
- S_n=\frac{a(1-r^n)}{1-r}
- Euler constant: \gamma
=\displaystyle\lim_{n\to\infty}
(\displaystyle\sum_{k=1}^n
\frac{1}{k}-\ln (n+1))
=\displaystyle\lim_{n\to\infty}
(\displaystyle\sum_{k=1}^n
\frac{1}{k}-\ln n)
- \begin{array}{c|l}X&x_1&x_2
&x_i&\cdots\\ \hline P&P_1&P_2
&P_i&\cdots\end{array}
E((X-\mu)^2)=E(X^2-2\mu X+\mu^2)
=E(X^2)-E(2\mu X)+E(\mu^2)
>Top 13. Least squares method:
- E(a,b)=\displaystyle\sum_{i=1}^n(y_i-ax_i-b)^2
- \cases{\frac{\partial E(a,b)}{\partial a}=-2\displaystyle\sum_i x_i(y_i-ax_i-b)=0\\\frac{\partial E(a,b)}{\partial b}=-2\sum_i (y_i-ax_i-b)=0}
⇔\cases{a\displaystyle\sum_ix_i^2+b\sum_ix_i=\sum_ix_iy_i...(*1)
\\a\sum_ix_i+bn=\sum_iy_i...(*2)}
from (*2): a\frac{\sum x_i}{n}+b=\frac{\sum y_i}{n}
=a\bar{x}+b=\bar{y}...(*3)
- replace to (*1): a\sum x_i^2+(-a\bar{x}+\bar{y})\sum x_i
=\sum x_iy_i
→a\big(\frac{\sum x_i^2}{n}-\bar{x}\frac{\sum x_i}{n}\big)
=\frac{\sum x_iy_i}{n}-\bar{y}\frac{\sum x_i}{n}
=a\big(\overline{x^2}-\bar{x}^2\big)
=\overline{xy}-\bar{y}\bar{x}
\therefore\;a=\frac{\overline{xy}-\bar{x}\bar{y}}{\overline{x^2}-\bar{x}^2}=\big(\frac{\sigma_{xy}}{\sigma_x^2}\big)
- →b=-a\bar{x}+\bar{y}
- ¶Data (2,3), (4,7), (9,11): find the least squared line:
- \mu_X=\frac{2+4+9}{3}=5,\;\mu_Y=\frac{3+7+11}{3}=7
\sigma_X^2=\frac{9+1+16}{3}=\frac{26}{3}
Cov(X,Y)=E[XY]-\mu_X\mu_Y=\frac{6+28+99}{3}-35=\frac{28}{3}
- →a=\frac{Cov(X,Y)}{\sigma_x^2}=\frac{28}{3}\frac{3}{26}=\frac{14}{13}
→b=-a\mu_X+\mu_Y=7-\frac{14}{13}・5=\frac{21}{13}
\therefore\;y=\frac{14}{13}x+\frac{21}{13}
13. 最小二乗法:
>Top 14. xxxx:
14. xxxx:
>Top 15. xxxx:
15. xxxx:
>Top 16. xxxx:
16. xxxx:
>Top 17. xxxx:
17. xxxx:
>Top 18. xxxx:
18. xxxx:
>Top 19. xxxx:
19. xxxx:
Comment
- a
- a
N(μ,σ2) |
Memorandum of Probablity Statistics |
Cat: SCI |
Compiled by Kanzo Kobayashi |
20726u |
Title |
Memorandum of Probality Statistics |
確率統計学メモ |
Index |
|
|
Tag |
; ; ; ; ; ; ; ; ; ; ; ; ; ; | |
Why |
||
Original resume |
Remarks |
>Top 0. Preface:
|
1. 序文
|
>Top 1. Basic knowledge:
|
2. 基礎知識:
|
>Top 2. Moment-generating function:
|
2. 積率母関数:
|
>Top 3. Normal Distribution (ND):
|
3. 正規分布:
|
>Top 4. Binomial distribution:
|
4. 二項分布:
|
>Top 5. Beta distribution:
|
5. ベータ分布:
|
>Top 6. Poisson distribution:
|
6. ポアソン分布:
|
>Top 7. Geometric distribution:
|
7. 幾何分布:
|
>Top 8. Exponential distribution:
|
8. 指数分布:
|
>Top 9. Hypergeometric disribution:
|
9. 超幾何分布:
|
>Top 10. Cauchy distribution:
|
10. コーシー分布:
|
>Top 11. Markov chain:
|
11. マルコフ連鎖:
|
>Top 12. Infinite series:
|
12. 無限級数:
|
>Top 13. Least squares method:
|
13. 最小二乗法: |
>Top 14. xxxx: |
14. xxxx: |
>Top 15. xxxx: |
15. xxxx: |
>Top 16. xxxx: |
16. xxxx: |
>Top 17. xxxx: |
17. xxxx: |
>Top 18. xxxx: |
18. xxxx: |
>Top 19. xxxx: |
19. xxxx: |
Comment |
|
|