Memorandum of Mathematical Physics
Cat: SCI
Pub: 2011
#2010
Takumi (of Yobinori)
20625u
Original resume
Remarks
>Top 0. Preface:
- LaTex is convenient in writing of mathematical expression, though it need some kind of patience.
0. 序文:
>Top 1. Equation of motion (EOM):
- ¶1: Free-fall motion:
- md2rdt2=F [2nd-order LDE]
- my″=−mg [m=mass]
→y′=−gt+C→y=−gt2+Ct+C′
y′(0)=0→C=0;y(0)=y0=C′ [initial condition]
- ∴y(t)=−12gt2+y0
- ¶2: >Top Parabolic motion:
- {mx″=0my″=−mg
- mx″=0→x″=0→x′=C=v0cosθ
- x(0)=0→C′=0
- x=Ct+C′=v0cosθt [uniform linear motion]
- my″=−mg→y″=g→y′=−gt+C=−gt+v0sinθ
- ∴y=−12gt2+v0sinθt+C′
- y(0)=0=C′→y(t)=−12gt2+v0sinθt [uniform acceleration motion]■
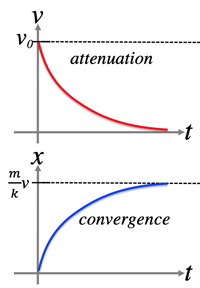
- ¶3: Motion with air resistance:
- mx″=−kx′
- let: x′=v→mv′=−kv→v′=−kmv
- v(0)=v0=C→v(t)=v0e−kmt
- x′=vv0e−kmt
→x=−kmv0e−kmt+C′
- x(0)=0→\;C'=\frac{m}{k}v_0
- ∴x(t)=mkv0(1−e−kmt)■
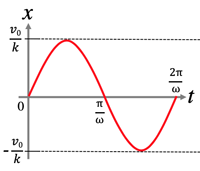
- ¶4: >Top Simple harmonic motion:
- mx″=−kx...(*) [k: sprint constant; x: displacement from equilibrium position]
→x″=−kmx=−ω2x;$here,\omega=\sqrt{\frac{m}{k}}$
- assume GS of (*): x=C1sint+C2cost=Csinωt1+C2cosωt [linear combination]
- →x=Csinωt1+C2cosωt
- initial condition: {x(0)=0x′(0)=v0
→{C2=0C1ω=V0
- →C1=v0ω,C2=0
- ∴x(t)=v0ωsinωt■
- ¶5: Uniform circular motion:
- [r0=raidus, ω0=angular velocity]
- v=r′er+rϕ′eϕ=0・er+r0ω0eϕ=r0ω0eϕ
- a=(r″−rϕ′2)er+(rϕ″+2r′ϕ′)eϕ=−r0ω20er=−v20r02er
- [using EOM]
F=ma=−mr0ω20er [centripetal]
1. 運動方程式:
- radial direction: 動径方向
- azmuthal direction: 方位角方向 <Ar. as-sumut
- pendulum isochronism: 振り子の等時性
- r(x): trace of position:
- to know r(t) by integration
- ¶3.
- Harmonic Motion:
- Polar coordinate system:
{e′r=ϕ′ere′ϕ=−ϕ′er
- <Rec. cord.>
{r=xex+yeyv=x′ex+y′eya=x″ex+y″ey
- <Por. cord.>
{r=rerv=r′er+rϕ′eϕa=(r″−rϕ′2)er+(rϕ″+2r′ϕ′)eϕ
- Taylor expansion:
$\sin x=x-\frac{x^3}{3!}
+\frac{x^5}{5!}-\dots
>Top 2. Pendulum isochronism:
- Single pendulum: [|ϕ|<<1]
- [azmuth direction of EOM]
- m(rϕ″+2r′ϕ′)=−mgsinϕ=ml [m=mass; l=length of pendulum]
mlϕ″=−mgsinϕ...(*)
→ϕ″=−glsinϕ [sinϕ≃ϕ]
→ϕ″=−glϕ
let: ω=√gl:
→ϕ″=−ω2ϕ [=uniform circular motion]
- let: ϕ(t)=C1sinωt+C2cosωt
here: ϕ(0)=ϕ0,ϕ′=o [initial condition]
→C2=ϕ0,C1ω=0→C1=0,C2=ϕ0 [ω≠0]
∴ϕ(t)=ϕ0cosωt■
- here: T=2πω=2π√lg[T=period]
- Exact solution of single pendulum:
- multiply ϕ′:ϕ″ϕ′+glϕ′sinϕ=0
→ddt(12ϕ2−glcosϕ)=0
→12ϕ2−glcosϕ=E [E=constant; mechanical energy]
- when: θ=θ0,→θ′=0
→E=−glcosθ0
→12ϕ′2−gl(cosϕ−cosϕ0)
→ϕ′2=2gl(cosϕ−cosϕ0)
here: ϕ′=−√2gl(cosϕ−cosϕ0)[0≤ϕ≤ϕ0]
- T=4∫T40dt=4∫0ϕ01−√2gl(cosϕ−cosϕ0)dϕ
=2√2lg∫ϕ001√cosϕ−cosϕ0dϕ
- change of variables: θ such that sinϕ2=sinϕ02sinθ
→T=4√lg∫π20dθ√1−sin2ϕ02sin2θ
- substitute to: sin(ϕ02)=a
T=4ω∫π20dθ√1−a2sin2θ=4ωK(a)[K:complete elliptic integral 1st]∗1
2. 振り子の等時性:
- complete elliptic integral of the 1st kind: 第1種完全楕円積分
- ∗1第1種完全楕円積分:
- F(x,k)=∫x0dt√(1−t2)(1−k2t2)
- F(x,0)=∫x01√1−t2dt=sin−1x
- F(x,1)=∫x011−t2dt=tanh−1x
= >Top 3. Conservation law:
- Momentum conservation law:
- md2rdt2=F
- P=mdrdt\; [P=momentum]
→dpdt=F→P(t2)−P(t1)=∫t2t1F(t)dt
P(t2)−P(t1)=I [I=impulse=change of momentum]
- when I=0:→P(t2)=P(t1) [conservation of momentum]
- Energy conservation law:
- W=Fcosθ・s=FS[Inner vector: W=work is constant]
- dW=F・dr [W is changeable]
→W=∫cF・dr
- conservative force: W=∫rr0F・dr
- potential energy: U(r)=−∫rr0Fdr
- Kinetic energy:
- k=12m|v|2=12m(v2x+v2y+v2z)
→dkdt=mv・dvdt
- v=drdt,mdvdt=F→dkdt=F・drdt
→∫t2t1dkdtdt=∫t2t1Fdrdtdt
k(t2)−k(t1)=∫cFdr
- ∴Δk=W
- energy conservation law: k(t2)−k(t1)=∫cFdr
- [F=conservative force]:
∫cFdr=∫r2r1Fdr=∫r2r0Fdr−∫r1r0Fdr=−U(r2)+U(r1)
- mechanical energy:
k(t2)−k(t1)=−U(r2)+U(r1)
∴k(t2)+U(r2)=k(t1)+U(r1)
- If F is conservative force, the potential energy is defined as:
U(r)=−∫rr0Fr...(*)
then, U(r′)−U(r)=−∫r′r0Fdr−(−∫rr0Fdr=−(∫r0rFdr+∫r′r0Fdr)=−∫r′rFdr
- thus, conservative force: W=−ΔU
- ¶1: Potential energy & Force [1 dimension]:
- U(x)=−∫xx0F(x)dx
- U(x+Δx)−U(x)=−∫x+ΔxxF(x)dx≃−F(x)Δx
→F(x)=−limΔx→0U(x+Δx)−U(x)Δx=−U(x)dx
- ¶2: Potential energy & Force [3D]
- U(r)=−∫rr0F(r)dr
- U(x+Δx,y+Δy,z+Δz)−U(x,y,z)≃−(FxΔx+FyΔy+FzΔz)
- when: Δy=Δz=0
→U(x;Δx,y,z)−U(x,y,z)≃−FxΔx
∴Fx=−limΔx→0U(x;Δx,y,z)−U(x,y,z)Δx
- thus: {Fx=−∂U(r)∂xFy=−∂U(r)∂yFz=−∂U(r)∂z
- ∴F(r)=(−∂U(r)∂x,−∂U(r)∂y,−∂U(r)∂z)=−(∂∂x,∂∂y,∂∂z)U(r)=−∇U(r)
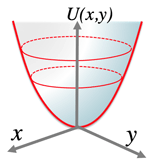
- ¶3: Harmonic oscillation (2D):
- U(x,y)=12k(x2+y2)
Fx=∂(x,y))∂x=−kx
Fy=∂(x,y))∂y=−ky
→F(r)=−k(x,y)=−kr
- ∇=(∂∂x,∂∂y,∂∂z)→∇×F=0
3. 保存則:
- momentum: 運動量
- impulse: 力積
- inner product/vector product: 内積/外積
- conservative force: 保存力
- gradient: 勾配
- harmonic oscillator: 調和振動子 =spring
- integration by substitution: 置換積分
- Harmonic oscillator:
- >Top Vector product:
a×b=(aybz−azby,azbx−axbz,axby−aybx)
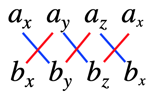
>Top 4. Damped oscillation:
- Damping oscillation:
- mx″=−kx−bx′ [k=spring constant; b=damping coefficient]
→x″=−ω20x−2γx′[ω0=√km,;γ=b2m]...(*)
- assume:x=eλt=−ω20eλt
→λ+2γλ+ω20=0
→λ±=−ω±√γ2−ω20[λ is -real number]
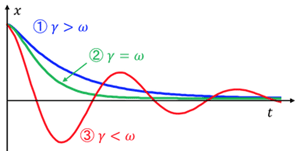
- 1) when: γ>ω0: [over-damped]
assume GS of (*) is x=C1eλ+t+C2eλ−t
here: x(0)=a,x′(0)=0 [exponentially damped]
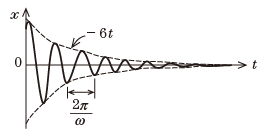
- 2) when: γ<ω0:
λ±=−γ±√γ2−ω20=−γ±i√ω20−γ2=−γ±iω
assume GS of (*) is x=C1e−γ+iw)t+C2e−γ−iw)t
=e−γt(C1eiωt+C2e−iωt)
=e−γt((C1+C2)cosωt+i(C1−C2)sinωt)
=e−γt(Acosωt+iBsinωt)=Ce−ωtcos(ωt+ϕ);
[C=√A2+B2,tanϕ=−BA]
- 3) when: γ=ω0
λ+=λ−=−λ
- >Top assume GS of (*) is x=C(t)e−γt
then, →x′=C′e−γt−C(γe−γt)
x″=C″e−γt−2C′(γe−γt)+C(γ2e−γt)
substitute to (*):
C″e−γt−2γC′e−γt+γ2Ce−γt=−ω20Ce−γt+2γ2e−γt−2γC′e−γt
C″+C(ω2−γ2)=0[e−γt≠0]
→C″=0[ω20−γ2=0]
→C=At+B ∴x=(At+B)e−γt[critical damping]
- Energetic consideration:
mx″=−kx−bx′
→mx″x′=akx′x−bx′2
→ddt(12mv2+12kx2)=−bv2<0 [mechanical energy]
−bv2→−bvdxdt [work efficient]
- >Top Forced oscillation:
mx″=−kx+Fcosωt
x″=−w20x+fcosωt...(*) [w0=√km,f=Fm]
- assume SS of (*): x=acosωt
- substitute to (*): −aω2cosωt=−aω20cosωt+fcosωt
→a=−fω2−ω20
SS of (*) is x=−fω2−ω20cosωt [resonance]
- GS of (*)=GS of homo.eq + SS of (*)
assume GS of (*): x=Asinω0t+Bcosω0t−fω2−ω20cosωt
- consider: ω→ω0;initial condition: x(0)=0,x′(0)=0
→a=0,B=fω2−ω20
→x=fω2−ω20(cosω0t−cosωt)
→x=−2f(ω+ω0)(ω−ω0)
sinω0+ω2tsinω0−ω2t
- here: ω0−ω=Δω
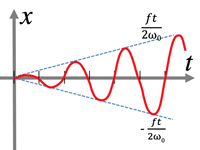
x=2fω0+ωsinω0+ω2tt2sinΔω2tΔω2t
Δω→0x=ft2ω0sinω0t [increasing ]
4. 減衰振動:
- damped oscillation/vibration: 減衰振動
- damping coefficient:
- over-damped: 過減衰
- critical damping: 臨界減衰
- restoring force: 復元力
- external force: 外力
- forced oscillation: 強制振動
- resonance: 共振・共鳴
- Euler's formula:
eiθ=cosθ+isinθ
- Damping oscillation:
- Critical damping:
- limx→0sinxx=1
- Forced oscillation:
>Top 5. Conservation law of angular momentum:
- moment of force (torque):
- N=r×F[r=distance from the origin]
- conservation of angular momentum:
L=r×p[L=angular momentum; p=momentum]...(*)
- differentiate (*): dLdt=drdt×p+r×dpdt=v×mv+r×F here $[\frac{dr}{dt}=v,\;\frac{p}{dt}=F]
- ∴dLdt=N[N=torque]
thus, when F∥r,N=0
dLdt=0→L=C [conservation of angular momentum]
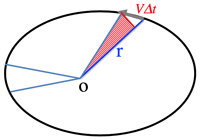
- Law of constant area velocity:
- ΔS=12rvΔtsinϕ
→ΔSΔt=12rvsinϕ...(*)
- while: angular momentum of planetary movement:
L=rmvsinϕ[L=angular momentum]...(**)
L=2mΔSΔt;[ΔSΔt=area velocity]
→\;[constant area velocity is one of law of constant angular momentum]
5. 角運動量保存則:
- angular momentum: 角運動量
- moment of force: 力のモーメント
- 外積の微分:
- ddt(a×b)=dadt×b+a×dbdt
- Constant area velocity: ΔS=vΔtsinϕ
>Top 6. Inertial Frame:
- Inertial/Noninertial frame:
- r=R+r0
substitute to mr″=F:
m(R″+r″0)=F→mr″0=F−mR″...(*)
- when, O0 is R=Vt [uniform linear motion]
→R′=V,R″=0
substitute to (*): mr″0=F→S0 is inertial frame.
- right side of (*) F−mR″ looks like a kind of force: [inertial force]
- >Top Equivalence principle:
- Fg=mgg[mg=gravitational mass]
- while: mia=F[mi=inertial mass]
- in only gravitational field: mia=mgg→a=mgmig
regardless of any object: a=g→mg=mi [equivalence principle]
6. 慣性系:
- noninertial frame: 非慣性系
- uniform linear motion: 等速直線運動
- equivalence principle: 等価原理
- Inertial frame:
-
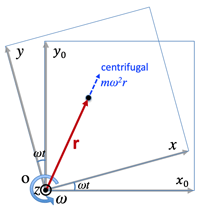
>Top 7. Coriolis Force:
- Rotating coordinate system:
- r=xoeox+yoeoy=xex+yey...(*)
here: {ex=cosωteox+sinωteoyey=−sinωteox+cosωteoy
→{e′x=−ωsinωteox+ωcosωteoy=ωeye′y=−ωcosωteox−ωsinωteoy=−ωex
→{e″x=−ω2exe″y=−ω2ey
- here EOM of (*): F=mr″
→r″=x″ex+y″ey+2(x′e′x+y′e′y)+xe″x+ye″y
→=x″ex+y″ey+2ω(x′ey−y′ex)−ω2(xex+yey)
- substitute to (*)mr″=F+mω2r+2mω(y′ex−x′ey)
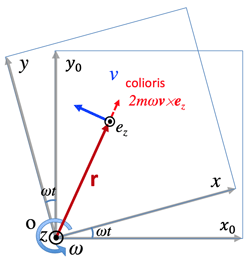
- here: mω(y′ex−x′ey)=2mωv×ez [Coriolis force]
7. コリオリの力:
- Coriolis force: コリオリの力
- apparent force: 見かけの力
- centrifugal force: 遠心力
- {v=(x′,y′,z′)ez=(0,0,1)
→v×ez=(y′−x′)
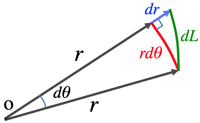
>Top 8. Archimedean spiral:
- Length in polar coordinates:
- dL=√(rdθ)2+(dr)2...(*1)
→=√r2+(drdθ)2dθ[r=f(θ)]
- from (*1):
- L=∫π0√r2+(drdθ)2dθ
→=∫π0√θ2+1dθ
- let θ=sinht→dθ=coshtdt
L=∫T0√sinh2t+1coshtdt
=∫T0cosh2tdt=∫T01+cosh2t2dt
=12[t+12sinh2t]T0
=12T+14sinh2T
=12T+12sinhTcoshT
=12log(π+√π2+1)+12π√π2+1≃6.1099
- Re:
- θ=et−e−12→(et)2−2θet−1=0
→et=θ+√θ2+1→t=log(θ+√θ2+1)
- θ0→πt0→log(π+√π2+1)=T
- sinhT=π[←θ sinht]
- coshT=√sinh2T+1=√π2+1
8. アルキメデスの螺旋:
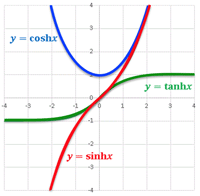
>Top 9. Hyperbolic function:
- Hyperbolic function:
- sinhx=ex−e−12
- coshx=ex+e−12
- tanhx=
- (sinhx)′=coshx
- cosh2x−sinh2x=1
- cosh2x=1+cosh2x2
- sinh2x=2sinhxcoshx
- comparison:
- cosh2x−sinh2x=1cos2x+sin2x=1tanhx=sinhxcoshxtanx=sinxcosx1−tanh2x=1cosh2x1+tan2x=1cos2x
- (sinhx)′=coshx(sinx)′=cosx(coshx)′=sinhx(cosx)′=−sinx(tanhx)′=1cosh2x(tanx)′=1cos2x
- sinh(x+y)=sinhxcoshy+coshxsinhysin(x+y)=sinxcosy+cosxsiny
- parametric:
- x=coshθ,y=sinhθ→x2−y2=1 [hyperbola]
- cf: x=cosθ,y=sinθ→x2+y2=1 [circle]
- Euler's formula:
- eiθ=cosθ+isinθ
- →cosθ=eiθ+e−iθ2
→sinθ=eiθ−e−iθ2i
9. 双曲線関数:
- hyperbolic function: 双曲線関数
- catenary: 懸垂線
>Top 10. Inverse trigonometric function:
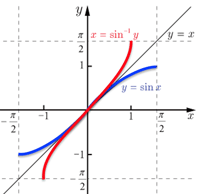
- y=arcsinx[−1≤x≤1,−π2≤y≤π2]
- x=siny→dxdy=cosy=√1−sin2y
→dydx=1√1−sin2y=1√1−x2
- y=arccosx[−1≤x≤1,0≤y≤π]
- x=cosy→dxdy=−siny=−√1−cos2y
→dydx=−1√1−cos2y=−1√1−x2
- y=arctanx[−∞≤x≤∞,−π2≤y≤π2]
- x=tany→dxdy=1cos2y=1+tan2y
→dydx=11+tan2y=11+x2
10: 逆三角関数:
>Top 11. Two-particle system motion:
- EOM:
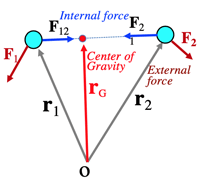
- m1r″1=F1+F12...(1)
- m2r″2=F2+F21...(2)
- (1)+(2): m1r″1+m2r″2=F1+F2
here: rG=m1r1+m2r2m1+m2=m1r1+m2r2M
[G=center of gravity; M=total mass]
→Mr″G=F1+F2 [external force only]
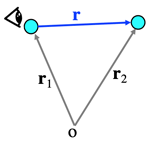
- >Top relative vector: r=r2−r1 [viewpoint from r1]
- r″=r″2−r″1=F2+F21m2−F1+F12m1=(1m1+1m2)F21+F2m2−F1m1
=1μ+F2m2+F1m1
[μ: reduced mass]
- →μr″=F21+μm2F2−μm1F1
→μr″=F21 [unless external force]
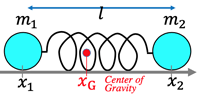
- Motion of connected objects: (>Fig.)
- motion of center of gravity: Mx″G=0 [constant linear motion]
- relative motion: μx″=−k(x2−x1−l) [μ: reduced mass]
here: ω=√kμ [simple oscillation]
- Total momentum:
- P=p1+p2=m1r′1+m2r′2
- P′=m1r″1+m2r″2=F1+F2
→P′=0→P=C [unless external force]
- Total kinetic energy:
- K=k1+k2=12m1r′21+12m2r′22...(*)
- here: {rG=m1r1+m2r2Mr=r2−r1
→{r1=rG−m2Mrr2=rG+m1Mr
- substitute to (*):
K=12m1(rg−m2Mr)2+12m2(rg+m1M)2
→=12(m1+m2)r′2G+12m1m2(m1+m2)Mr′2
→=12Mr′2G+12μMr′2 [momentum of COG & reduced mass]
- Total angular momentum:
- L=L1+L2=r1×p1+r2×p2=r1×m1r′1+r2×m2r′2...(*)
- →L′=r′1×m1r′1+r1×m1r″1+r′2×m2r′2+r2×m2r″2
=r1×(F1+F12)+r2×(F2+F21)
=(r2−r1)×F21+r1×F1+r2×F2=r1×F1+r2×F2 [each torque]
- consider COG and substitute to (*):
L=(rG−m2Mr)×m1(r′G−m2Mr′)+(rG+m1Mr)×m2(r′G+m2Mr′)
=m1rG×r′G−m1m2MrG×r′−m1m2Mr×r′G+m1m22M2r×r′
+m2rG×r′G+m1m2MrG×r′+m1m2Mr×r′G+m21m2M2r×r′
=rG×(m1+m2)r′G+r×m1m2(m1+m2)M2r′
- ∴L=rG×Mr′G+r×μr′ [torque of COG and torque of relative vector]
11. 二粒子系の運動:
- relative vector: 相対位置ベクトル
- reduced mass: 換算質量
- total momentum: 全運動量
- center of gravity: COG
- >Top Commutative law of vector product:
a×(b+c)=a×b+a×c
- <Summary>:
- EOM of COG:
- Mr″G=F1+F2
- Relative EOM:
- μr″=F21 [no ex-force]
- Total momentum:
- P=p1+p2
P=constant [without ex-force]
- Total kinetic energy:
- K=k1+k2
12Mr′2G+12μr′2
- Total angular momentum:
- L=L1+L2
=r×Mr′G+r×μr′
- L′=N1+N2 [torque]
>Top 12. Rigid body dynamics:
- Rigid body: deformation is zero or negligible; the distance between any two point remains constant regardless of external forces exerted; continuous distribution of mass.
- Rigid body of EOM:
- P′G=F [EOM of COG]
- L′=N [rotation around the axis passing COG]
- EOM of COG:
- mir″i=fi+∑jFfij[ex−power+in−power;i≠j]
- here; Mr″G=∑imiri∑imi [COG]
- feature: 1) degree of freedom: 3n→6; 2) offset of internal-power
- Mr″G=∑ifi
- here: PG=Mr′G,F=∑ifi
P′G=F
- Rotary motion:
- P′i=fi+∑jfij[momentum=exforce+inforce]→\;r_i\times P_i'=r_i\times (f_i+\sum_jf_{ij})\;
ri×p′i=ddt(ri×pi)...(*1)
- ∵ddt(ri×pi)=r′i×pi+ri×p′i...(*2)
here: r′i×pi=0 [parallel vector]
- here: ∑i∑j(ri×fij)=∑i>j(ri−rj)×fij=0
- ∵ifn=3→∑i∑j(ri×fij)
=r1×f12+r1×f13+r1×f21+r1×f23+r1×f31+r1×f32=0
- from (*2): ddt∑i(ri×pi)=∑i(ri×fi)...(*3)
from (*3): L′=∑i(ri×pi);N=∑i(ri×fi)= [L= angular momentum; N=moment of force]
∴L′=N [around the origin]
- Relative position from COG:
- here;rG=∑imiriM;r′G=∑imiriM=frac∑ipiM
- substitute to (*3): ri=ro+rG
→ddt∑i((roi+rG)×pi)=∑i((roi+rG)×fi)
→ddt∑i(roi×pi)+ddt∑i(rG×pi)=∑i(roi×fi)+∑i(rG×fi)...(*4)
- here: ddt∑i(rG×pi)=∑i(r′G×pi+rG×p′i)=∑i(rG×p′i)
- here: p′i=fi+∑jfij=fi
- (*4) is: ddt∑i(roi×pi)=∑i(roi×fi)
- →p′oi=pi−mir′G
→ddt∑i(r′i×(p′i+mir′G))=∑i(roi×fi)
→ddt∑i(roi×p′oi)+ddt((∑imiroi)×r′G)=∑i(roi×fi)
- here: ∑imiroi=∑i(ri−rG)=∑imiri−rG∑imi=0
- here: Lo=∑iroi×poi;No=∑i(roi×fi)
∴L′o=No [rotary motion around COG]
12. 剛体の力学:
- rigid body: 剛体
- point mass: 質点
- point of application: 作用点
- line of action: 作用線
- degree of freedom: 自由度
- manifold: 多様体
- deformation: 変形
- nonlocal action; action at a distance: 遠隔作用
- roll/yaw/pitch: position of a rigid body
- Rotation around the axis passing COG:
- ddt(ri×pi)=r′i×pi+ri×p′i
here; r′i×pi=0
- Relative position:
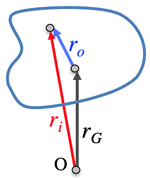
- 原点:
L′=N
- 重心:
L′o=No
>Top 13. Inertia moment of rigid body:
- Inertia moment:
- Motion with fixed axis: →degree of freedom is 1.
- L′z=Nz
- here: Lz=∑i(ri×pi)z=∑i(xiy′i−yix′i)=∫ρ(r)(xy′−yx′)d3r..(*)
- here: x=rcosϕ,y=rsinϕ
x′=−rϕ′sinϕ,y′=rϕ′cosϕ
→xy′−yx′=r2ϕ′cos2ϕ+r2ϕ′sin2ϕ=r2ϕ′
- substiture to (*): Lz=(∫r2ρ(r)d3r)ϕ′
=Izϕ′[inertia moment around z-axis]
∴Izϕ″=Nz [I_z: difficulty of rotation]
- Inertia moment of COG:
- I=∫r2ρ(r)d3r...(*2)
- >Top Parallel axes theorem:
I=IG+Mh2 [M=total mass; h=distance between axes]
- here: ro=r−rG
- substitute to (*2): I=∫r2ρ(r)d3r
=∫(x2+y2)ρ(r)d3r
=((xo+xg)2+(yo+yG)2)ρ(r)d3r
=(x2g+y2g)∫ρ(r)d3r+2xg∫xoρ(r)d3r
++2yg∫yoρ(r)d3r+∫(x2o+y2o)ρ(r)d3r
- here: ∫xoρ(r)d3r=∫(x−xG)ρ(r)d3r
=∫xρ(r)d3r−xg∫ρ(r)d3r=Mxg−xgM=0
- ∴I=Ig+Mh2
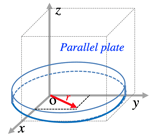
- >Top Orthogonal axes theorem:
- Iz=∈r2σ(r)d3r=∫(x2+y2)σ(r)d2r
=∫x2σ(r)d2r+∫y2σ(r)d2r=Iy+Ix
- ∴Iz=Ix+Iy
13. 剛体の慣性モーメント:
- inertia moment: 慣性モーメント
- orthogonal axis: 直交軸
- Parallel axis theorem:
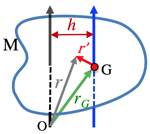
- Orthogonal axis:
>Top 14. Mechanical energy of rigid body:
- Kinetic energy of rigid body:
- ∑i12mi|r′i|2
=∑i12mi|r′oi+r′G|2
=12∑imi|r′G|2+∑imir′oir′G+12∑imi|roi|2
=12|r′g|2+rg(∑imir′oi)+12∑imi|roi|2
=translational motion + kinetic energy around COG [∵∑imiroi=0]
- here [motion around fixed axis passing COG]
12∑imi|r′oi|2=12∑imi(riω)2
=12ω2∑imir2i=12ω2∫r2ρ(r)d3r
=12Iω2
- ∴K=12Mv2G+12Iω2 [translational.e+rotational.e]
- Potential energy of rigid body:
- ∑imigzi=g∑imizi=MgzG
∴U=Mgh [h=height of COG from the origin]
14. 剛体の力学的エネルギー:
- translational motion: 並進運動
>Top 15. Matrix exponential:
- Proof:
- e0=E+0+1202+⋯=E
- ddteAt=ddt(E+At+12(At)2+⋯)
=0+A+A2t+12!A3t2+cdots
=A(E+At+12!A2+cdots)=AeAt
- ¶ ddty(t)=Ay(t)
- →y(t)=eAty0[y0=y(0)]
15. 行列指数関数:
- matrix exponential: 行列乗
- commutative: 可換
- Maclaurin expansion:
ex=1+x+12!x2+13!x3+⋯
=∞∑k=01k!xk
- eA=∞∑k=01k!Ak [A=square matrix]
- e0=E
- ddteAt=AeAt
- if AB=BA→eAeB=eA+B
>Top 16. Chauchy's functional equation:
- definition: f(x+y)=f(x)+f(y)...(*) [real continuous function]
- is f(x)=ax the only function to satisfy (*)?]
- proof:
- when x=y=0→f(0)=f(0)+f(0)→f(0)=0 [cross the origin]
- when y=−x→f(0)=f(x)+f(−x)→f(x)=−f(x) [odd function]...(*2)
- when n is natural number, and x is real number, then f(nx)=nf(x)
- when n=1 is established.
- if n=k is established, then replace x→kx and y→x
then,
f(kx+x)=f(kx)+f(x)=kf(x)+f(x)
- ∴f((k+1)x)=(k+1)f(x) is established.
- then, any n of natural number: f(nx)=nf(x)
- from (*2), substitute: x→nx, then f(−nx)=−f(nx)=−nf(x)[−n: negative number]
→f(mx)=mf(x) [m: integer]
- when rational number r=mn:
→nf(rx)=f(nrx)=f(mx)=mf(x)
→f(rx)=mnf(x)=rf(x)...(*3)
substitute to (*3): x=1→f(r)=rf(1)
let f(1)=a then: f(r)=ar[x:rational number]
- ∃{qn} such that ∀x=limn→∞qn=x[{qn}: rational series] and f(x) is continuous function.
→f(x)=limn→∞f(qn)=limx→∞aqn=ax
∴f(x)=ax■
- when: f(x) is continuous function, then consider 'rational number' only: [density]
- when x is real number, which is expressed as follows:
x=m+∞∑i=1Ci10−i[m,Ci: integer, 0≤Ci≤9]
- rational series: qn=m+n∑i=1Ci10−i→x(n→∞)
16. コーシーの関数方程式:
- real function: 実関数
- mathematical induction: 数学的帰納法
- density: 稠密性
- 数学的帰納法, mathematical induction:
- base case: show f(0) is clearly true.
- inductive step: show for any k≥0, if f(k) holds, then f(k+1) also holds.
>Top 17. Taylor expansion:
- f(x)=f(a)+f′(a)(x−a)+12!f″(a)(x−a)2+13!f‴(a)(x−a)3+⋯...(*)
- where: h=x−a, then (*) is:
f(a+h)=f(a)+f′(a)h+12!f″(a)h2+13!f‴(a)h3+⋯
[Taylor expansion around a]
- where: a=0=x→f(x)=f(0)+f′(0)x+12!f″(0)x2+13!f‴(0)x3+⋯
=∞∑n=0f(n)(0)n!xn
[Maclaurin expansion]
- ¶1: f(x)=exx=0...(*)
- to find linear function in the vicinity of (*):
f(0)=1,f′(0)=1→g(x)=1+x
- to find quadratic function in the vicinity of (*):
$f(0)=1,\; f'(0)=1,\;f''(0)=1→\; g(x)=1+x+\frac{1}{2}x^2
- ex=e0+e0x+12!e0x2+13!e0x3+14!e0x4+⋯
=1+x+12!x2+13!x3+14!x4+15!x5+⋯
∴ex=∞∑n=01n!xn
- log(1+x)=x−12x2+13x3−14x4+⋯=infty∑n=0(−1)nn+1xn+1
- f(x)=log(1+x)→f(n)(x)=
- log2=1−12+12−12+⋯=∞∑n=1(−1)n−1n=log2[Mercator series]
- (1+x)n=1+nx+n(n−1)2!x2+n(n−1)(n−2)3!x3+⋯
- sinx=x−13!x3+15!x5−17!x7+⋯
f(0)=sin0=0,f′(0)=cos0=1,f″=−sin0=0,f‴=−cos0=−1,⋯
sinx=0+1x+02!x2+13!x3+14!x4+⋯
=0+1x+02!x3+−13!x5−04!x6+⋯
=x−13!x3+15!x5−17!x7+⋯
∴sinx=∞∑n=0(−1)n(2n+1)!x2n+1
- cosx=1−12!x2+14!x4−16!x6+⋯
∴cosx=∞∑n=1(−1)n(2n)!x2n
- tanx=x+13x3+215x5+⋯
- Euler's formula:
- isinx=ix−i13!x3+i15!x5−i17!x7+⋯
eix=1+ix−12!x2−i13!x3+14!x4+i15!x5−⋯
- →eix=cosx+isinx [Euler' formula]
→cosx=eix+e−ix2,sinx=eix−e−ix2
- ei(a+b)=eiaeib
→cos(a+b)+isin(a+b)=(cosa+isina)(cosb+isinb)
=(cosacosb−sinasinb)+i(cosasinb+sinacosb) [addition theorem]
- einθ=(eiθ)n
cos(2θ)+isin(2θ)=(cosθ+isinθ)2
(cos2θ−sin2θ)+i2cosθsinθ [double-angle formula]
- cos(3θ)+isin(3θ)=(cosθ+isinθ)3
=(cos3θ−3cosθsin2θ)+i(3cos2θsinθ−sin3θ)
=(4cos3θ−3cosθ)+i(3sinθ−4sin3θ) [tripple-angle formula]
- sin2(x2)=(eix2−e−ix22i)2=eix+e−ix−2−4=1−cosx2 [half-angle formula]
- cos2(x2)=(eix2+e−ix22)2=eix+e−ix+24=1+cosx2
- cosasinb=eia+e−ia2・eib−e−ib2i
=ei(a+b)−e−i(a+b)−ei(a−b)+e−i(a−b)4i
=12(ei(a+b)−e−i(a+b)2i−ei(a−b)−e−i(a−b)2i)=12(sin(a+b)−sin(a−b))[sum of products]
- cosacosb=12(cos(a+b)+cos(a−b))
- sinasinb=−12(cos(a+b)−cos(a−b))
- sinacosb=12(sin(a+b)+sin(a−b))
- eia+eib=ei(a+b)2ei(a−b)2+ei(a+b)2e−i(a−b)2
=ei(a+b2(ei(a−b)2+e−i(a−b)2)
=(cos(a+b2)+isin(a+b2))・(cos(a−b2)+isin(a−b2)+cos(a−b2)−isin(a−b2))
=2cos(a−b2)(cos(a+b2)+isin(a+b2))
=2cos(a−b2)cos(a+b2)+i2cos(a−b2)sin(a+b2)
- while eia+eib=(cosa+isina)+(cosb+sinb)
=(cosa+cosb)+i(sina+sinb)→
- cosa+cosb=2cos(a+b2)cos(a−b2) [product of sum]
- cosa−cosb=−2sin(a+b2)sin(a−b2)
- sina+sinb=2sin(a+b2)cos(a−b2)
- sina−sinb=2cos(a+b2)sin(a−b2)
17. テイラー展開:
- radius of convergence: 収束半径
- : ダランベールの収束判定法
- d'Alembert's ratio test:
limn→∞|an+1an|=r
- r<1: convergence
- r>1: divergence
>Top 18. Fourier expansion:
- continuous f(x) defined in 0≤x≤2π can be expressed by the combination of trigonometric funtions, i.e.:
- f(x)=c+∞∑n=1(ancos(nx)+bnsin(nx))...(*1)
- where c is the average of (*1): c=12π∫2π0f(x)dx...(*2)
- coefficient an,bn can be:
{an=1π∫2π0f(x)cos(nx)dxbn=1π∫2π0f(x)sin(nx)dx
- where, n=0 of (*2): $→\;c=\frac{1}{2}a_0
- so, \boxed{f(x)=\frac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}
\bigl(a_n\cos (nx)+b_n\sin (nx)\bigr)}...(*3) [Fourier series]
- here: \displaystyle\int_0^{2\pi}\cos(mx)\cos(nx)dx
=\frac{1}{2}\displaystyle\int_0^{2\pi}\bigl(\cos(m+n)x+\cos(m-n)x\bigr)dx
=\frac{1}{2}\left[\frac{1}{m+n}\sin (m+n)x+\frac{1}{m-n}\sin (m-n)x\right]_0^{2\pi}=\pi \delta_{mn}\;
[Kronecker delta: \delta_{mn}=1\;(m=n),\;0\;(m\ne n)]
- similarly: \displaystyle\int_0^{2\pi}\sin (mx)\sin (nx)dx=\pi\delta_{mn}
- \displaystyle\int_0^{2\pi}\sin (mx)\cos (nx)dx=0
18. フーリエ展開:
>Top 19. Linear algebra:
- Gaussian elimination method:
- multiply 1st row: -\frac{d}{a} then add to 2nd row:
\pmatrix{a&b&c\\d&e&f\\g&h&i}\;
- multiply 1st row: -\frac{g}{a} then add to 3rd row:
\pmatrix{a&b&c\\0&e'&f'\\g&h&i}\;
- multiply 1st row: -\frac{g}{a} then add to 3rd row:
\pmatrix{a&b&c\\0&e'&f'\\0&h'&i'}\;
- multiply 2nd row: -\frac{h'}{e'} then add to 3rd row:
\pmatrix{a&b&c\\0&e'&f'\\0&0&i''}\;
- Cofactor expansion:
- \pmatrix{a&b&c&d&\\0&e&f&g\\0&0&h&-i&\\0&0&0&j}=a・e・h・j
- |A|=a_{i1}\tilde{a}_{i1}+a_{i2}\tilde{a}_{i2}+\cdots+a_{in}\tilde{a}_{in}
=\displaystyle\sum_{j=1}^na_{ij}\tilde{a}_{ij}
=a_{1j}\tilde{a}_{1j}+a_{2j}\tilde{a}_{2j}+\cdots+a_{nj}\tilde{a}_{nj}
=\displaystyle\sum_{i=1}^na_{ij}\tilde{a}_{ij}
- Properties of matrix (elementary row operations):
- Row switching:
- R_i \leftrightarrow R_j
- Scalar times:
- row multiplication: kR_i→R_i, \;\mathrm{where}\;k≠0
- row additon: R_i+kR_j\leftrightarrow R_i, \;\mathrm{where}\; i≠j
- invere of matrix: T_{ij}^{-1}=T_{ij}
- same two rows makes the matrix is 0.
- k times of a row and then add it to other row makes no change of the matrix.
- Commutative law:
- AB\ne BA
- (A+B)+C=A+(B+C)
- Associative law: A(BC)=(AB)C
- Indenty matrix:
- E=\pmatrix{1&0&0\\0&1&0\\0&0&1}
- AE=A,\; EA=A
- >Top Inverse matrix:
- BA=E→\;A^{-1}A=E→\;AA^{-1}=E\; [regular matrix]
- from Cramer's rule:
- \pmatrix{a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}}
\pmatrix{x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\
x_{31}&x_{32}&x_{33}}
=\pmatrix{1&0&0\\0&1&0\\0&0&1}
- x_{11}=\frac{\tilde{a}_{11}}{|A|},\;
x_{21}=\frac{\tilde{a}_{12}}{|A|},\;
x_{31}=\frac{\tilde{a}_{13}}{|A|},\;
- X=\frac{1}{|A|}\pmatrix{\tilde{a}_{11}&\tilde{a}_{21}&\tilde{a}_{31}\\
\tilde{a}_{12}&\tilde{a}_{22}&\tilde{a}_{32}\\
\tilde{a}_{13}&\tilde{a}_{23}&\tilde{a}_{33}}
=\frac{1}{|A|}^tA^{ij}
- A=\pmatrix{a&b\\c&d},\; A^{-1}=\frac{1}{ad-bc}\pmatrix{d&-b\\-c&a}
- Matrix multiplication :
- |AB|=|A||B|
- |AA^{-1}|=|A||A^{-1}|=1→\;|A^{-1}|=\frac{1}{|A|}
- >Top Linearly dependent:
- if there exist scalars a_1,a_2,\cdots,a_n , not all zero, such that:
- a_1\mathbf{v}_1+a_2\mathbf{v}_2+\cdots+a_n\mathbf{v}_n=\mathbf{0}...(*)
- \mathbf{v}_1=\frac{-a_2}{a_1}\mathbf{v}_2+\cdots+\frac{-a_n}{a_1}\mathbf{v}_n\; [if a_1≠0]
thus \mathbf{v}_1 is shown to be a linear combination of the remaining vectors.
- a sequence of vectors (\mathbf{v}_1,\mathbf{v}_2,\cdots,\mathbf{v}_n) is linearly independent if (*) can only be satisfied by a_i=0 for i=1,\cdots,n. this implies that no vector in the sequence can be represented as a linear combination of the remaining vectors.
- \displaystyle\sum_{i=1}^na_i\mathbf{v}_i=\mathbf{0} \Rightarrow a_1=\cdots=a_n=0
- a certain vector \mathbf{x} can be uniquely expressed by linear combination of linearly independent vectors (\mathbf{v}_1,\mathbf{v}_2,\cdots,\mathbf{v}_n).
- >Top Rank of a matrix A:
- is the maximum number of linearly independent row of vectors of the matrix: rank A=n
- is the dimension of the image of the linear map represented by A; which is converted to number of the rank dimension.
- by simplification of a square matrix, if ^\exists EA, then ^\exists A^{-1}
- eg.: B=\pmatrix{1&0&1\\-2&-3&1\\3&3&0}=\pmatrix{1&0&1\\0&-3&3\\0&0&0}:
- the first two columns linearly independent, but the third is a linear combination of the first two; thus the rank is 2.
- when the upper triangle matrix B has a column (or row) of all 0 elements (=rank down); the rank is n-1, here 3.
- Trace: sum of its diagonal entries.
- tr(AB)=\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^na_{ij}b_{ij}
=\mathrm{tr}(BA)
- tr(A)=\mathrm{tr}(^tA)
- >Top Transposed matrix:
- A=\pmatrix{a_{11}&\cdots&a_{1n}\\ \vdots&&\vdots\\a_{m1}&\cdots&a_{mn}}
- ^tA=\pmatrix{a_{11}&\cdots&a_{m1}\\ \vdots&&\vdots\\a_{1n}&\cdots&a_{mn}}
- ^{tt}A=A,\;^t(A+B)=^tA+^tB,\;^t(kA)=k^tA,\; ^t(kA+lB)=k^tA+l^tB,\;^t(AB)=^tB^tA
- (square matrix): ^t(A^{-1})=(^tA)^{-1},\; \mathrm{tr}A=\mathrm{tr}^tA
- \mathrm{det} A=\mathrm{det}^tA
- \langle Ax,y\rangle=\langle x,^tAy\rangle
- Coordinates transformation:
- \pmatrix{p_x&q_x&r_x\\p_y&q_y&r_y\\p_z&q_z&r_z}\pmatrix{x'\\y'\\z'}
=\pmatrix{x\\y\\z}
→\;\pmatrix{x'\\y'\\z'}
=\pmatrix{p_x&q_x&r_x\\p_y&q_y&r_y\\p_z&q_z&r_z}^{-1}\pmatrix{x\\y\\z}
- \pmatrix{p_x&q_x&r_x\\p_y&q_y&r_y\\p_z&q_z&r_z}\pmatrix{x'\\y'\\z'}
=\pmatrix{s_x&t_x&u_x\\s_y&t_y&u_y\\s_z&t_z&u_z}\pmatrix{x\\y\\z}
→\;\pmatrix{x'\\y'\\z'}
=\pmatrix{p_x&q_x&r_x\\p_y&q_y&r_y\\p_z&q_z&r_z}^{-1}
\pmatrix{s_x&t_x&u_x\\s_y&t_y&u_y\\s_z&t_z&u_z}\pmatrix{x\\y\\z}
- >Top Eigenvalue and eigenvector:
- \bf{Ax}=\lambda \bf{x}\;[x: eigenvector]
\bf{Ax}-\lambda \bf{Ex}=0→\;(\bf{A}-\lambda \bf{E})\bf{x}=0
(\bf{A}-\lambda \bf{E})=0\; [x\ne 0; Eigen equation]
\lambda=\lambda_i,\;(i=1,2,\cdots,n)\; [eigenvalue]
solve: (A-\lambda_iE=0)x=0\; [n-unknown simul.linear.eq]
→\;x=x_\;(i=1,2,\cdots,n)\; [eigenvector]
- ¶1:A=\pmatrix{2&3\\4&1}
\pmatrix{2-\lambda&3\\4&1-\lambda}=(2-\lambda)(1-\lambda)-12
→\;=(\lambda-5)(\lambda+2)=0\;\therefore\;\lambda=5, -2
- i) when: \lambda=5:→\;\pmatrix{-3&3\\4&-4}\pmatrix{x\\y}
=\pmatrix{0\\0}
\Leftrightarrow \\cases{-3x+3y=0\\4x-4y=0}
\Leftrightarrow x-y=0
x=s_1:, y=s_1→\;x_1=s_1\pmatrix{1\\1} \; (s_1≠0)
- ii) when: \lambda=-2:→\;\pmatrix{4&3\\4&3}\pmatrix{x\\y}
=\pmatrix{0\\0}
\Leftrightarrow 4x+3y=0
x=-3s_2:, y=4s_2→\;x_2=s_2\pmatrix{-3\\4} \; (s_2≠0)
- ¶2:A=\pmatrix{2&1$1\\1&2$1\\1&1&2}
\pmatrix{2-\lambda&1$1\\1&2-\lambda&1\\1&1&2-\lambda}
=-(\lambda-1)^2(\lambda-4)
→\therefore\;\lambda=1, 4
- i) when: \lambda=1:→\;\pmatrix{1&1&1\\1&1&1\\1&1&1}\pmatrix{x\\y\\z}
=\pmatrix{0\\0\\0}
\Leftrightarrow x+y+z=0
x=s_1:, y=t_1→\;z=-s_1-t_1
→\;x_1=\pmatrix{s_1\\t_1\\-s_1-t_1} \; (s_1, t_1≠0)
=s_1\pmatrix{1\\0\\-1}+t_1\pmatrix{0\\1\\-1}
- ii) when: \lambda=4:→\;\pmatrix{-2&1&1\\1&-2&1\\1&1&-2}\pmatrix{x\\y\\z}
=\pmatrix{0\\0\\0}
→\left(\begin{array}{ccc|c}1&0&-1&0\\0&1&-1&0\\0&0&0&0\\\end{array}\right)
\cases{x-z=0\\y-z=0}→\;x=y=z=s_2→\;s_2\pmatrix{1\\1\\1}
- >Top Diagonalization-I (no-double solution):
- diagonalizable square matrix A:
- Diagonal matrix of A exists in the form of:
P^{-1}AP=\pmatrix{\lambda_1&&&0\\&\lambda_2&&\\
&&\ddots&\\0&&&\lambda_n\\}\; [P\; is transformation matrix; \lambda_n\; eigenvalue]
- (P^{-1}AP)^n=\underbrace{(P^{-1}AP)(P^{-1}AP)\cdots(P^{-1}AP)}_{n}=P^{-1}A^nP\therefore\;A^n=P(P^{-1}A^nP)P^{-1}
- Formula:
where, linearly independent eigenvector
(x_1,x_2,\cdots,x_n) of a square matrix A:
let P=(x_1,x_2,\cdots,x_n) then,
P^{-1}AP=\pmatrix{\lambda_1&&&0\\&\lambda_2&&\\
&&\ddots&\\0&&&\lambda_n\\}\; [P\; is transformation matrix; \lambda_n
- Proof: P has inverse matrix:
C_1x_1+C_2x_2+\cdots+C_nx_n=(x_1,x_2,\cdots,x_n)
\pmatrix{C_1\\C_2\\\vdots\\C_n}=0\;
[n-dimensional simultaneous linear eq.] ...(*)
if rank(P<0), then (*) has the solution other than trivial one (C_1=C_2=\cdots=C_n=0), which contracts linearly independence of x_1,x_2,\cdots,x_n; thus rank (P)=n→\;P is regular matrix.
- Proof-2: being diagonal matrix:
P^{-1}AP^=P^{-1}A(x_1,x_2,\cdots,x_n)=P^{-1}(Ax_1,Ax_2,\cdots,Ax_n)
=P^{-1}(\lambda_1x_1,\lambda_2x_2,\cdots,\lambda_nx_n)
=P^{-1}(x_1,x_2,\cdots,x_n)\pmatrix{\lambda_1&&&0\\&\lambda_2&&\\
&&\ddots&\\0&&&\lambda_n\\}\; [P=(x_1,x_2,\cdots,x_n)]
- here cf.: (\lambda_1x_1,\lambda_2x_2)
=\pmatrix{\lambda_1x_1&\lambda_2x_2\\\lambda_1y_1&\lambda_2y_2}
=\pmatrix{x_1&x_2\\y_1&y_2}\pmatrix{\lambda_1&0\\0&\lambda_2}
- Formula:
where,
eigenvector x_1,x_2,\cdots,x_k corresponding different eigenvalue of \lambda_1,\lambda_2,\cdots,\lambda_k of n-sized square matrix A is linearly independent. (1≤k≤n)...(*0)
- Proof:
when k=1, (*0) is obvious. [c_1x_1=0,\; x_1≠\mathbf{0}→\;c_1=0]
assume k=m
(*) is true, and consider: C_1x_1+C_2x_2+\cdots+C_mx_m+C_{m+1}x_{m+1}=0...(*1)
multiply A
to (*1) from left:
→\;C_1\lambda_1x_1+C_2\lambda_2x_2+\cdots+
C_m\lambda_mx_m+C_{m+1}\lambda_{m+1}x_{m+1}=0...(a)
multiply \lambda_{m+1} to (*1) from left:
→\;C_1\lambda_{m+1}x_1+C_2\lambda_{m+1}x_2+\cdots+
C_m\lambda_{m+1}x_m+C_{m+1}\lambda_{m+1}x_{m+1}=0...(b)
(a)-(b):C_1(\lambda_1-\lambda_{m+1})x_1
+C_2(\lambda_2-\lambda_{m+1})x_2+\cdots
+C_m(\lambda_m-\lambda_{m+1})x_m=0
here: x_1,x_2,\cdots,x_m
is linearly independent, then:
C_i(\lambda_i-\lambda_{m+1})=0,\;(i=1,2,\cdots,m)
here: \lambda_i-\lambda_{m+1}≠0,\; (i=1,2,\cdots,m)
→\;C_1=C_2=\cdots=C_m=0
substitute this to (*1): →\;C_{m+1}x_{m+1}=0→\;C_{m+1}=0
thus, x_1,x_2,\cdots,x_{m+1}
is linearly independent.
- ¶1: diagonalize: A=\pmatrix{-2&1\\5&2}
- \pmatrix{-2-\lambda&1\\5&2-\lambda}=(-2-\lambda)(2-\lambda)-5
=(\lambda-3)(\lambda+3)=0→\;\lambda03, -3
- i) when \lambda=3:
\pmatrix{-5&1\\5&-1}\pmatrix{x\\y}=\pmatrix{0\\0}
\Leftrightarrow -5x+y=0
→\;x=x_1,\;y=5s_1→\;x_1=s_1\pmatrix{1\\5}
- ii) when \lambda=-3
\pmatrix{1&1\\5&5}\pmatrix{x\\y}=\pmatrix{0\\0}
\Leftrightarrow x+y=0→\;x=s_2, \;y=-s_2→\;x_1=s_2\pmatrix{1\\-1}
thus: P=\pmatrix{1&1\\5&-1} then P^{-1}AP=\pmatrix{3&0\\0&-3}
- check: P^{-1}=\frac{1}{-6}\pmatrix{-1&-1\\-5&1}
=\frac{1}{6}\pmatrix{1&1\\5&-1}
→\;P^{-1}AP=\frac{1}{6}\pmatrix{1&1\\5&-1}
\pmatrix{-2&1\\5&2}\pmatrix{1&1\\5&-1}
- here: \frac{1}{6}\pmatrix{1&1\\5&-1}\pmatrix{-2&1\\5&2}\bigl(\bigr)
=\frac{1}{6}\pmatrix{3&3\\-15&3}\pmatrix{1&1\\5&-1}
=\frac{1}{6}\pmatrix{18&0\\0&18}=\pmatrix{3&0\\0&-3}
- Diagonalization-II (double solution):
- diagonalize square matrix A=\pmatrix{-2&2&4\\-2&3&2\\-2&1&4}
\pmatrix{-2-\lambda&2&4\\-2&3-\lambda&2\\12&1&4-\lambda}
=-(\lambda-1)(\lambda-2)^2=0→\;\lambda=1,\;2(double)$
- i) \lambda=1:
\pmatrix{-3&2&4\\-2&2&2\\-2&1&3}\pmatrix{x\\y\\z}
=\pmatrix{0\\0\\0}→\;x_1=s_1\pmatrix{2\\1\\1}
- ii) \lambda=2
\pmatrix{-4&2&4\\-2&1&2\\-2&1&2}\pmatrix{x\\y\\z}
=\pmatrix{0\\0\\0}\;\Leftrightarrow -2x+y+2z=0→\;x=s_2,\;z=t_2, y=2s_2-2t_2
→\;x_2=s_2\pmatrix{1\\2\\0}+t_2\pmatrix{0\\-2\\1}
- here: \pmatrix{2\\1\\1},\;\pmatrix{1\\2\\0},\;\pmatrix{0\\-2\\1} are linealy independent, and eigenvector.
- p^{-1}AP=\pmatrix{1&0&0\\0&2&0\\0&0&2}
- Diagonalization-III (no diagnalizable case)
- A=\pmatrix{-3&-1\\1&-1}
\pmatrix{-3-\lambda&-1\\1&-1-\lambda}=(-3-\lambda)(-1-\lambda)+1
=\lambda^2+4\lambda+4=(\lambda+2)^2=0→\;\lambda=-2\; (double)
\Leftrightarrow x+y=0→\;x=s_1,\;y=-s_1 →\; x_1=s_1\pmatrix{1\\-1}
there is no other independent eigenvector than this: thus 'no diagonal'
19. 線形代数:
- Gaussian elimination: ガウスの消去法, 掃き出し法
- identity (unit) matrix: 単位行列
- upper triangle matrix: 上三角行列
- cofactor expansion: 余因子展開
- rank: 階数
- trace: 跡, 対角線成分
- linear combination: 線形結合
- transposed matrix: 転置行列
- coordinate transformation: 座標変換
- eigenvalue: 固有値
- eigenvector: 固有ベクトル
- diagonalization: 対角化
- diagonalizable: 対角化可能
- regular matrix =reversible matrix: 正則行列 (=可逆行列)
- transformation (=diagonalizable) matrix: 変換(=対角化)行列
- 掃き出し法:
- 余因子展開:
- 特徴:
- スカラー倍
- 可換法則
- 結合法則
- 単位行列
- 乗算
- 線形独立(=一次独立)
- ランク, 階数
- 転置行列
- 逆行列, Inverse matrix:
- make ^tA
- make \tilde{A}
- consider sgn \tilde{A}
- 座標変換:
- 固有値と固有ベクトル:
- 対角化:
>Top 20. Delta function:
- Paul Dirac's delta function:
- definition-1: \delta(x-a)=\cases{\infty,\;(x=a)\\0,\;(x≠0)}
- definition-2: \int_{-\infty}^{\infty}f(x)\delta(x-a)dx=f(a)
- when f(x)=1→\;\int_{-\infty}^{\infty}\delta(x-a)dx=1 [size of infinity]...(*)
- point mass of a mass m on x=a:\;\int_{-\infty}^{\infty}m\delta(x-a)dx=m
- but, mathematically (*) normal function will be zero; which is called distribution (by Schwarz) or hyperfunction (by Sato).
20. デルタ関数:
- point mass: 質点
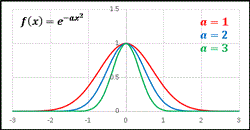
>Top 21. Gaussian integration:
- Definition: \boxed{\displaystyle\int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi}}
- proof: I=\displaystyle\int_{-\infty}^{\infty}e^{-x^2}dx
- I^2=(\displaystyle\int_{-\infty}^{\infty}e^{-x^2}dx)
(\displaystyle\int_{-\infty}^{\infty}e^{-y^2}dy)\;[x↔y]
=\displaystyle\int_{-\infty}^{\infty}\displaystyle\int_{-\infty}^{\infty}e^{x^2+y^2}dxdy
- let: x=r\cos\theta,\;y=r\sin\theta, then
I^2=\displaystyle\int_0^{2\pi}\displaystyle\int_0^{\infty}e^{-r^2}rdrd\theta
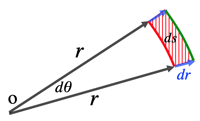
- surface integral: ds=\pi(r+dr)^2\frac{d\theta}{2\pi}-\pi r^2\frac{d\theta}{2\pi}
=rdrd\theta+\frac{1}{2}(dr)^2d\theta \simeq rdrd\theta
- I^2=\displaystyle\int_0^{2\pi}d\theta\displaystyle\int_0^{\infty}re^{-r^2}rd
=2\pi\left[-\frac{1}{2}e^{-r^2}\right]_0^{\infty}=\pi\;→I=\sqrt{\pi},\;(I>0)
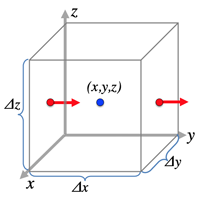
- Net outflow:=(\frac{\partial V_x}{\partial x}+\frac{\partial V_y}{\partial y}
+\frac{\partial V_z}{\partial z}
)\Delta x\Delta y\Delta z
- thus outflow per volume: =div \mathbf{V}
21. ガウス積分:
>Top 22. Vector analysis:
- Divergence: outflow-inflow
- V_x(x+\frac{\Delta x}{2},y,z)\Delta y\Delta z-V_x(x-\frac{\Delta x}{2},y,z)\Delta y\Delta z
=\bigl(V_x(x+\frac{\Delta x}{2},y,z)-V_x(x-\frac{\Delta x}{2},y,z)\bigr)\Delta y\Delta z...(*)
- Taylor expansion: f(a+h)=f(a)+f'(a)h+\frac{1}{2!}f''(a)h^2+\cdots
- Vx(x±\frac{\Delta x}{2},y,z)\simeq Vx(x,y,z)
±\frac{\partial V_x}{\partial x}\frac{\Delta x}{2}
- (*)\simeq\bigl(V_x(x,y,z)+\frac{\partial V_x}{\partial x}\frac{\Delta x}{2}
-V_x(x,y,z)
+\frac{\partial V_x}{\partial x}\frac{\Delta x}{2}\bigr)\Delta y\Delta z
=\frac{\partial V_x}{\partial x}
\Delta x\Delta y\Delta z
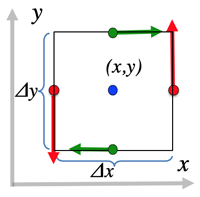
- >Top Rotation:
- Definition: rot \mathbf{V}
=\bigl(\frac{\partial V_z}{\partial y}-\frac{\partial V_y}{\partial z},
\frac{\partial V_x}{\partial z}-\frac{\partial V_z}{\partial x},
\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y}\bigr)
=\nabla \times \mathbf{V}\;
[\nabla=(\frac{\partial }{\partial x}, \frac{\partial }{\partial y}, \frac{\partial }{\partial z})]
- =\bigl(V_y(x+\frac{\Delta x}{2},y)-V_y(x-\frac{\Delta x}{2},y)\bigr)\Delta y
+\bigl(V_x(x,y-\frac{\Delta y}{2})-V_x(x,y+\frac{\Delta x}{2})\bigr)
\Delta x
\simeq \bigl(V_y(x,y)+\frac{\partial V_y}{\partial x}\frac{\Delta x}{2}
-V_y(x,y)+\frac{\partial V_y}{\partial x}\frac{\Delta x}{2}\bigr)\Delta y
+\bigl(V_x(x,y)-\frac{\partial V_x}{\partial y}\frac{\Delta y}{2}
-V_x(x,y)-\frac{\partial V_x}{\partial y}\frac{\Delta y}{2}\bigr)\Delta x
=(\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y})\Delta x\Delta y
- per unit space: =\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y}
\; [z-component of rot\;\mathbf{V}]
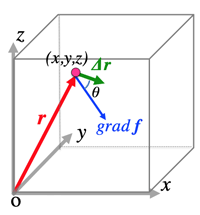
- Gradient:
- Definition: grad f=(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y},
\frac{\partial f}{\partial z})\;[grad f means mostly† increasing direction]
- Proof (†):\Delta f=f(r+\Delta r)-f(r)
=f(x+\Delta x, y+\Delta y, z+\Delta z)-f(x,y,z)
\simeq f(x,y,z)+\frac{\partial f}{\partial x}\Delta x
+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
=(\mathrm{grad}\;f)・\Delta r=|\mathrm{grad}\;f||\Delta r|\cos\theta
≤|\mathrm{grad}\;f||\Delta \mathbf{r}|\; [\theta=0\;maximum]
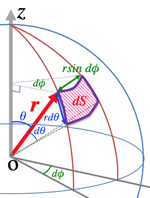
- >Top Solid angle: (unit: Steradian d\Omega)
- dS=r^2\sin\theta d\theta d\phi
d\Omega\equiv \frac{dS}{r^2}=\sin\theta d\theta d\phi
- ¶1: [global surface]
=\displaystyle\int_0^{2\pi}\displaystyle\int_0^{\pi}\sin\theta d\theta d\phi=4\pi
- ¶2: [\theta_1→\theta_2,\;\phi_1→\phi_2]
=(\phi_2-\phi_1)(\cos\theta_1-\cos\theta_2)
- ¶3: [half-apex angle=\alpha]
=\displaystyle\int_0^{2\pi}\displaystyle\int_0^{\alpha}\sin\theta d\theta d\phi
=2\pi(1-\cos\alpha)
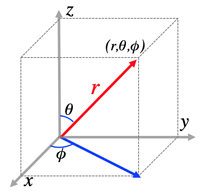
- >Top Spherical coordinates:
- \cases{x=r\sin\theta\cos\phi\\y=r\sin\theta\sin\phi\\z=r\cos\theta}
\cases{r=\sqrt{x^2+y^2+z^2}\;(0≤r)\\\theta=\cos^{-1}(\frac{z}{\sqrt{s^2+y^2+z^2}})
\;(0≤\theta ≤\pi)
\\\phi=\mathrm{sgn}(y)\cos^{-1}(\frac{x}{\sqrt{x^2+y^2}})\;
(0≤\phi<2\pi) }
- here: sgn(y)=\cases{1\;(0≤y)\\-1\;(y<0)}
22. ベクトル解析:
- vector field: ベクトル場
- position vector: 位置ベクトル
- solid angle: 立体角
- steradian: 立体角の単位 (sr)
>Top 23. Integration method:
- Some Calculus formula:
- y=fg\\
\log y=\log(fg)=\log f+\log g\\
\frac{y'}{y}=\frac{f'}{f}
+\frac{g'}{g}\\
y'=f'g+fg'
- y=(\frac{f}{g})
\log y=\log\frac{f}{g}
=\log f-\log
g\\
\frac{y'}{y}=\frac{f'}{f}
-\frac{g'}{g}\\
y'=\frac{f'}{g}-\frac{fg'}{g^2}
=\frac{f'g-fg'}{g^2}
- (e^x)'=e^x
- (a^x)'=a^x\log a
- y=(x^x)'
\log y=x\log x
\frac{y'}{y}=\log x+1\\
y'=y(\log x+1)=x^x(\log x+1)
- (\log x)'=\frac{1}{x}
- (\log y)'=\frac{y'}{y}
- (\log_ax)'\\
=(\frac{\log x}{\log a})'\\
=\frac{1}{\log a}(\log x)'\\
=\frac{1}{x\log a}
- Some Integral formula:
- \int\frac{1}{x}=\log|x|+C
- \int\frac{1}{x^2}=-\frac{1}{x}+C
- \int \frac{f'}{f}=\log|f|+C
- \int e^xdx=e^x+C
- \int a^x=\frac{a^x}{\log a}+C
- \int a^x\log adx=a^x+C
- \int\log xdx=\int x'\log xdx=x\log x-x(\log x)'dx=x\log x-\int dx
=x\log x-x+C\; [\log = 1・\log]
- \int \frac{1}{x\log a}dx=\log_ax
- \int \sin xdx=-\cos x+C
- \int \cos xdx=\sin x+C
- \int \tan xdx=\int \frac{\sin x}{\cos x}dx=-\int\frac{(\cos x)'}{\cos x}dx
=-log|\cos x|+C
- \int \sec^2xdx=\tan x+C
- \int \csc^2xdx=-cotx+C
- \int \frac{1}{\cos^2x}dx=\tan x+C
- \int \frac{1}{\sin^2x}dx=-\frac{1}{\tan x}+C
- \int\frac{1}{x^2+a^2}dx=\frac{1}{a}\tan^{-1}\frac{x}{a}+C,\;(a≠0)
- \int\frac{1}{\sqrt{x^2-a^2}}dx=\sin^{-1}\frac{x}{a}+C,\;(a>0)
- \int\frac{1}{\sqrt{x^2+a}}dx=\log |x+\sqrt{x^2+a}|+C,\;(a≠0)
- Integration by parts:
- \int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx
- ¶\int\log|x|dx=\int x'\log|x|dx=x\log|x|-\int x(\log|x|)'dx
=x\log|x|-\int x\frac{1}{x}dx=x\log|x|-x+C
- \int f(g(x))g'(x)dx= [differential contact type]
- let:g(x)=t
- \int \frac{f'(x)}{f(x)}dx=\log|f(x)|+C
- \int(f(x))^af'(x)dx=\frac{(f(x)^{a+1})}{a+1}+C
- ¶\int x^ne^xdx=x^ne^x-\int (x^n)'e^x
- ¶\int \frac{1}{\cos^3xdx}
=\int \frac{1}{\cos^2x}\frac{1}{\cos x}dx
=\tan x\frac{1}{\cos x}-\int \tan x\frac{\sin x}{\cos^2x}dx
=\frac{\sin x}{\cos^2x}-\int \frac{\sin^2 x}{\cos^3 x}
=\frac{\sin x}{\cos^2x}-\int \frac{1}{\cos^3x}dx+\int \frac{1}{\cos x}dx
2\int \frac{1}{\cos^3x}dx
=\frac{\sin x}{\cos^2x}+\frac{1}{2}\log\big|\frac{1+\sin x}{1-\sin x}\big|+C
- ¶\int (\log x)^3dx)
- t=\log x→\;dt=\frac{1}{x}dx→dx=e^tdt
=\int t^3e^tdt=t^3e^t-3t^2e^t+6te^t-6e^t+C=(t^3-et^2+6t-6)e^t+C
=\{(\log x)^3-(\log x)^2+6\log x-6\}x+C
- Integration by substitution:
- \int f(x)dx=\int f(g(t))g'(t)dt
- ¶\int_0^1x^2dx
=\int_0^2\frac{1}{4}t^2
\frac{1}{2}dt
- x=\frac{1}{2}t
- dx=\frac{1}{2}dt
- ¶\int_0^1\sqrt{1-x^2}dx...(*)
let:
x=\sin(u),\;dx=\cos udu
→\sqrt{1-x^2}=\cos(u)
=\int_0^{\frac{\pi}{2}}
\cos^2(u)
du
=(\frac{u}{2}+ \frac{\sin(2u)}{4})
\big|_0^{\frac{\pi}{2}}
=\frac{\pi}{4}
- ¶\int_a^b(x-a)(x-b)dx
=\int_a^b\{(x-a)^2-(b-a)(x-a)\}dx
=\frac{1}{3}(x-a)^3-(b-a)\frac{1}{2}(x-a)^2\big|_a^b=-\frac{1}{6}(b-a)^3
- ¶\int \frac{1}{\cos x}dx\; [→*tips]
=\int \frac{1+t^2}{1-t^2}\frac{2}{1+t^2}dt=\int \frac{2}{1-t^2}dt
=\int (\frac{1}{1+t}+\frac{1}{1-t})dt=\log |1+t|-\log |1-t|+C
=\log |\frac{1+t}{1-t}|+C
=\log \big|\frac{1+\tan\frac{x}{2}}{1-\tan\frac{x}{2}}\big|+C
- ¶\int \frac{1}{\sin x}dx\;...(*) [→*tips]
\frac{1}{\sin x}=\frac{\sin x}{1-\cos^2x},\; t=\cos x→dt=-sin xdx
(*)=\int \frac{\sin x}{1-t^2}\frac{1}{-\sin x}dt=\int \frac{1}{t^2-1}
=\frac{1}{2}\int (\frac{1}{t-1}-\frac{1}{t+1})dt
=\frac{1}{2}(\log|t-1|-log|t+1|)+C=\frac{1}{2}\log |\frac{t-1}{t+1}|+C
=\frac{1}{2}\log \big|\frac{1-\cos x}{1+\cos x}\big|+C
- Rotational body integral: around x-axis:
V=\pi\int_a^bf(x)^2dx
- Baumkuchen type integral (shell integration): around y-axis:
f(x)=g(x)-h(x)
V=2\pi\int_a^bxf(x)dx
- Pappus-Guildinus theorem:
volume of a solid revolution by roatating about an external axis (y):
- V=2\pi rS\; [r=distance from axis to the gravity, S=space of the graph]
- x_G=\frac{m_1x_1+m_2x_2+\cdots+m_nx_n}{m_1+m_2+\cdots+m_n}
=\frac{\int_a^b x\rho f(x)dx}{\int_a^b\rho f(x)dx}\; [\rho=specific density]
=\frac{\int_a^b xf(x)dx}{S}
- S=\displaystyle\int_a^b f(x)dx
- V=\int_a^b 2\pi xf(x)dx\; [Baumkuchen]
- x_G=\frac{\frac{V}{2\pi}}{S}\therefore\;\boxed{V=2\pi Sx_G}
- King property:
- \int_a^b f(x)dx=\int_a^b f(a+b-x)dx
effective when f(x)+f(a+b-x) is easily calculated.
- ¶1:\int_{-1}^1\frac{\sin^2(\pi x)}{1+e^x}dx...I
2I=\{\int_{-1}^1\frac{\sin^2(\pi x)}{1+e^x}
+\frac{\sin^2(\pi x)}{1+e^{-x}}\}dx
=\int_{-1}^1\sin^2(\pi x)dx=\int_{-1}^1\frac{1-\cos (2\pi x)}{2}dx
=\frac{1}{2}x-\frac{1}{4\pi}\sin(2\pi x)\big|_{-1}^1=1
\therefore\;I=\frac{1}{2}
23. 積分法:
- integration by substitution: 置換積分法
- integration by parts: 部分積分法
- Basic:
\sin(\frac{\pi}{2}-x)=\cos x
\cos(\frac{\pi}{2}-x)=\sin x
\sin(x+\frac{\pi}{2})=\cos x
\cos(x+\frac{\pi}{2})=-\sin x
\sin(x+\pi)=-\sin x
\cos(x+\pi)=-\cos x
- Addition formula:
\sin(a\pm b)=\sin a\cos b\pm \cos a\sin b
\cos(a\pm b)=\cos a\cos b\mp \sin a\sin b
\tan(a\pm b)=\frac{\tan a\pm\tan b}
{1\mp\tan a\tan b}
- Double angle formula:
\sin 2x=2\sin x\cos x
\cos 2x=\cos^2x-\sin^2x
=2\cos^2x-1=1-2\sin^2x
\tan 2x=\frac{2\tan x}{1-2\tan^2 x}
- Half angle formula:
\sin^2x=\frac{1}{2}(1-\cos 2x)
\cos^2x=\frac{1}{2}(x+\cos 2x)
\tan^2x=\frac{1-\cos 2x}{1+\cos 2x}
\tan x=\pm\frac{1-\cos 2x}{\sin 2x}
- Tripple angle formula:
\sin 3x=3\sin x-4\sin^3x
\cos 3x=-3\cos x+4\cos^3x
- Product-Sum formula:
\sin a\cos b=\frac{1}{2}\bigl(\sin(a+b)
+\sin(a-b)\bigr)
\sin a\sin b=\frac{1}{2}\bigl(-\cos(a+b)
+\cos(a-b)\bigr)
\cos a\cos b=\frac{1}{2}\bigl(\cos(a+b)
+\cos(a-b)\bigr)
- Sum-Product formula:
\sin a+\sin b=2\sin\frac{a+b}{2}
\cos\frac{a-b}{s}
\sin a-\sin b=2\cos\frac{a+b}{2}
\sin\frac{a-b}{s}
\cos a+\cos b=2\cos\frac{a+b}{2}
\cos\frac{a-b}{2}
\cos a-\cos b=-2\sin\frac{a+b}{2}
\sin\frac{a-b}{2}
- (\sin^{-1}x)'=\frac{1}{\sqrt{1-x^2}}
(\cos^{-1}x)'=-\frac{1}{\sqrt{1-x^2}}
(\tan^{-1}x)'=\frac{1}{1+x^2}
- >Top Integration by parts: (integral-first!)
- \int f^0g^0=f^0g^{-1}-\int f^1g^{-1}
=f^0g^{-1}-f^1g^{-2}+\int f^2g^{-2}
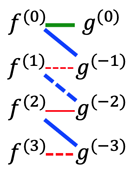
<*Tips>
- f(\sin x)\cos x→t=\sin x
→dt=\cos xdx
- f(\cos x)\sin x→t=\cos x
- f(\tan x)\frac{1}{\cos^2x}
→t=\tan x
→dt=\frac{1}{\cos^2x}dx
- f(\sin x,\;\cos x)...(*)
→t=\tan\frac{x}{2}
→\sin x=\frac{2t}{1+t^2}
→\cos x=\frac{1-t^2}{1+t^2}
→dt=\frac{1+t^2}{2}dx
\int(*)dx
=f(\frac{2t}{1+t^2},\;
\frac{1-t^2}{1+t^2})
\frac{2}{1+t^2}dt
- \int\log xdx→\int 1・\log xdx
- \int_0^{\pi}xf(\sin x)dx
=\frac{\pi}{2}\int_0^{\pi}f(\sin x)dx
- make square of trigonometry!
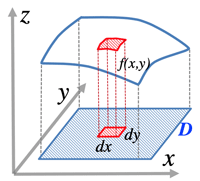
>Top 24. Multiple integral:
- Repeated integral:
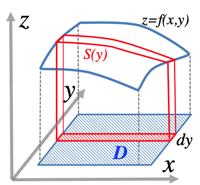
- \displaystyle\iint_D f(x,y)dxdy=\displaystyle\int_c^d\displaystyle\int_a^bf(x,y)dxdy
=\displaystyle\int_a^b\displaystyle\int_c^df(x,y)dydx
- ¶1: \displaystyle\iint_D(3x-y)dxdy,\;D=\{(xy)|0≤x≤1,\;-1≤y≤2|\}
- =\displaystyle\int_{-1}^2\displaystyle\int_0^1(3x-y)dxdy
=\displaystyle\int_{-1}^2\bigl[\frac{3}{2}x^2-yx\bigr]_0^1dy
=\displaystyle\int_{-1}^2(\frac{3}{2}-y)dy
=\bigl[\frac{3}{2}y-\frac{1}{2}y^2\bigr]_{-1}^2=3
- \displaystyle\int_0^1\displaystyle\int_{-1}^2(3x-y)dydx
=\displaystyle\int_0^1\bigl[3xy-\frac{1}{2}y^2\bigr]_{-1}^2dx
=\displaystyle\int_0^1(9x-\frac{3}{2})dx
=\bigl[\frac{9}{2}x^2-\frac{3}{2}x\bigr]_0^1=3
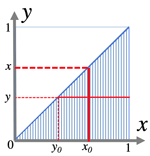
- ¶2: \displaystyle\iint_De^{x^2}dxdy,\;D=\{(x,y)|0≤y≤1,\;y≤x≤1\}
- =\displaystyle\int_0^1\displaystyle\int_y^1e^{x^2}dxdy [antiderivative?]
=\displaystyle\int_0^1\displaystyle\int_0^xe^{x^2}dydx
=\displaystyle\int_0^1\bigl[ye^{x^2}\bigr]_0^xdx
=\displaystyle\int_0^1xe^{x^2}dx=\bigl[\frac{1}{2}e^{x^2}\bigr]_0^1=\frac{1}{2}(e-1)
- Substitutive integral:
- ¶1: \displaystyle\iint_D\frac{1}{x^2+y^2}dxdy,\;D=\{(x,y)|1≤x^2+y^2≤4,\;y≥0\}
- =\displaystyle\int_0^{\pi}\displaystyle\int_1^2\frac{1}{r^2}rdrd\theta
=\displaystyle\int_0^{\pi}\bigl[\log r\bigr]_1^2d\theta
=\displaystyle\int_0^{\pi}\log 2\theta=\pi\log 2
- >Top Jacobian:
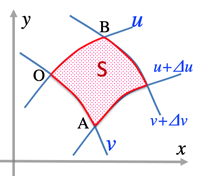
- 0\bigl(x(u,v),\;y(u,v)\bigr)
A\bigl(x(u+\Delta u,v),\;y(u+\Delta u,v)\bigr)
B\bigl(x(u,v+\Delta v),\;y(u,v+\Delta v)\bigr)
- x(u+\Delta u,v)\simeq x(u,v)+\frac{\partial x}{\partial u}\Delta u
- vec{OA}\simeq \bigl(\frac{\partial x}{\partial u}\Delta u,\;,
\frac{\partial y}{\partial u}\Delta u\bigr)
vec{OB}\simeq \bigl(\frac{\partial x}{\partial v}\Delta v,\;,
\frac{\partial y}{\partial v}\Delta v\bigr)
- \boxed{S\simeq \left|det\pmatrix{\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}}\right|\Delta u\Delta v
=J(u,v)\Delta u\Delta v}
- thus: \displaystyle\iint_D f(x,y)dxdy
=\displaystyle\iint_E f\left(x(u,v),\;y(u,v)\right)|J(u,v)|dudv
- ¶1: J(u,v) on polar coordinates:
- \cases{x=r\cos\theta\\y=r\sin\theta},\;\cases{u↔r\\v↔\theta}
- J(u,v)=\|det\pmatrix{\cos\theta&-r\sin\theta\\\sin\theta&r\cos\theta}\|=r
- ¶2: \displaystyle\iint_D (x-y)e^{x+y}dxdy,\;D=\{(x,y)|0≤x+y≤2,\;0≤x-y≤2\}...(*)
- let: x+y=u,\;v=x-y;\;\cases{x=\frac{1}{2}(u+v)\\y=\frac{1}{2}(u-v)}
- J(u,v)=\left|det\pmatrix{\frac{1}{2}&\frac{1}{2}\\\frac{1}{2}&-\frac{1}{2}}\right|
=\frac{1}{2}
- (*)=\displaystyle\int_0^2\displaystyle\int_0^2 ve^{u}\frac{1}{2}dudv
=\frac{1}{2}\displaystyle\int_0^2\bigl[ve^u\bigr]_0^2dv
=\displaystyle\int_0^2(ve^2-v)dv=\frac{1}{2}\bigl[\frac{1}{2}e^2v^2-\frac{1}{2}v^2\bigr]_0^2=e^2-1
24. 重積分:
- iterated/repeated integral: 累次積分
- substitutive integral: 置換積分
- antiderivative=primitive function: 原子関数
- Jacobian matrix: ヤコビ行列 J_f
>Top 25. XXXX:
25. XXXX:
>Top 26. YYYY:
26. YYYY:
>Top 27. ZZZZ:
27. ZZZZ:
Comment
- In studying effectively, it's important to accumulate in the manner of dicrete, heurisitic, empirical, and then formalized knowledge.
- 効率的に学ぶには、離散的、発見的、実証的、そして形式化した知識を集めることが肝要である。
Memorandum of Mathematical Physics |
Cat: SCI |
|
Takumi (of Yobinori) |
20625u |
Original resume |
Remarks |
|
>Top 0. Preface:
|
0. 序文: |
>Top 1. Equation of motion (EOM):
|
1. 運動方程式:
|
>Top 2. Pendulum isochronism:
|
2. 振り子の等時性:
|
= >Top 3. Conservation law:
|
3. 保存則:
|
>Top 4. Damped oscillation:
|
4. 減衰振動:
|
>Top 5. Conservation law of angular momentum:
|
5. 角運動量保存則:
|
>Top 6. Inertial Frame:
|
6. 慣性系:
|
>Top 7. Coriolis Force:
|
7. コリオリの力:
|
>Top 8. Archimedean spiral:
|
8. アルキメデスの螺旋: |
>Top 9. Hyperbolic function:
|
9. 双曲線関数:
|
>Top 10. Inverse trigonometric function:
|
10: 逆三角関数: |
>Top 11. Two-particle system motion:
|
11. 二粒子系の運動:
|
>Top 12. Rigid body dynamics:
|
12. 剛体の力学:
|
>Top 13. Inertia moment of rigid body:
|
13. 剛体の慣性モーメント:
|
>Top 14. Mechanical energy of rigid body:
|
14. 剛体の力学的エネルギー:
|
>Top 15. Matrix exponential:
|
15. 行列指数関数:
|
>Top 16. Chauchy's functional equation:
|
16. コーシーの関数方程式:
|
>Top 17. Taylor expansion:
|
17. テイラー展開:
|
>Top 18. Fourier expansion:
|
18. フーリエ展開: |
>Top 19. Linear algebra:
|
19. 線形代数:
|
>Top 20. Delta function:
|
20. デルタ関数:
|
>Top 21. Gaussian integration:
|
21. ガウス積分: |
>Top 22. Vector analysis:
|
22. ベクトル解析:
|
>Top 23. Integration method:
|
23. 積分法:
<*Tips>
|
>Top 24. Multiple integral:
|
24. 重積分:
|
>Top 25. XXXX: |
25. XXXX: |
>Top 26. YYYY: |
26. YYYY: |
>Top 27. ZZZZ: |
27. ZZZZ: |
Comment |
|
|