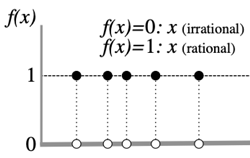
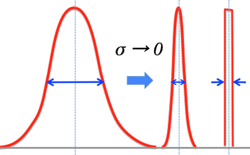
>Top 6. Ito's lemma and Stochastic differential equation:
- In 1940s, Ito's lemma is an identity used in the differential equation of a time-dependent function of a stochastic process. (Stochastic differential equation)
- The lemma is widely employed in mathematical finance, particularly of Black-Scholes equation for option values.
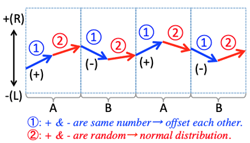
- $dx=Adt+Bdw$, where $Adt$ represents constant movement in $dt$, and $Bdw$ shows random movement ($B$ is strength of random, and $Bw(t)$ shows displacement magnitude.)
- In applying the above equation in economics, the first term $Adt$ shows general trend of growth to a constant direction.
- The above second term $Bdw$ shows volatility fluctuated by global market.
- Ito's lemma indicates the clear separation of the first (=trend) and second term (=volatility).
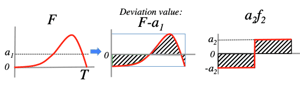
- >Top Taylor Expansion: (useful in making approximation)
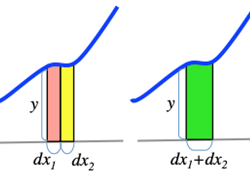
- $F(x_0+dx)=F(x_0)+\frac{dF(x_0)}{dx}dx+\frac{1}{2!}\frac{d^2F(x_0)}{dx^2}dx^2+
\frac{1}{3!}\frac{d^3F(x_0)}{dx^3}dx^3+\dots$
- The second term (of $dx^2$) has more significant function.
- Ito's lemma indicates:
- $dx=Adt+Bdw; \longrightarrow dy=F(Adt+Bdw)$ (trying to express $dy=F(dt)$)
- From Taylor Expansion:
$dy=\frac{dF}{dx}(Adt+Bdw)+\frac{1}{2}\frac{d^2F}{dx^2}(Adt+Bdw)^2+\dots)$
$dy=\frac{dF}{dx}Adt+\frac{dF}{dx}Bdw+\frac{1}{2}\frac{d^2F}{dx^2}
(A^2dt^2+2ABdtdw+B^2dw^2)+\dots$
- Neglection of small amount:
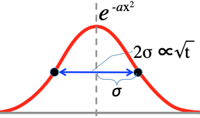
- Generally, $dw=\sqrt{dt}$ is assumed: [random walk expands $\propto\sqrt{t}$]
- If $dt=0.01; dw=0.1; dtdw=0.001; dt^2=0.0001; dw^2=0.01; dw^3=0.001$
- thus, we can leave $dt, dw, dw^2$.
- the above equation can be simplified neglecting small terms:
$dy=\frac{dF}{dx}Adt+\frac{dF}{dx}Bdw+\frac{1}{2}\frac{d^2F}{dx^2}B^2dw^2$
- as $dw^2=dt$
$dy=\left(\frac{dF}{dx}A+\frac{1}{2}\frac{d^2F}{dx^2}B^2\right)dt+\frac{dF}{dx}Bdw$ [variable separation]
- The above $w$ is the position changing part, and $dw^2$ cancels $+dw$ or $-dw$ position.]
- $F(x)$ should be correctly $F(x, t)$, then the above Ito's lemma equation will be:
$dy=\left(\frac{\partial F}{\partial x}A+\frac{\partial F}{\partial t}
+\frac{1}{2}\frac{\partial^2F}{\partial x^2}B^2\right)dt+\frac{\partial F}{\partial x}Bdw$
- Significance of Ito's lemma:
- when $dx=A_1dt+B_1dw$, then if $dy=A_2dt+B_2dw$ [the first term shows the world 'trend', while the second term 'volatility'.]
- from the the above equation:
- $A_2=\frac{dF}{dx}･A_1+\frac{1}{2}\frac{d^2F}{dx^2}･B_1^2$
- $B_2=\frac{dF}{dx}･B_1$
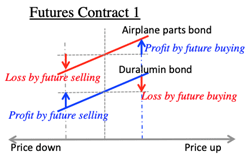
- Application to non-risk portfolio:
- when the price of duralumin bond is $x$, the price of airplane parts is $y$; $y=F(x)$
- from Ito's lemma equation,
- $dx=A_1dt+B_1dw$, then $B_2dw=\frac{dF}{dx}･B_1dw$
- thus, the risk of future buying of 1 unit of the airplane parts bond $y$ can be covered by the future selling of $\frac{dF}{dx}$ unit of duralumin bond.
|
6.
伊藤のレンマと確率微分方程式:
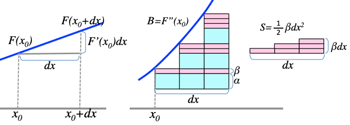
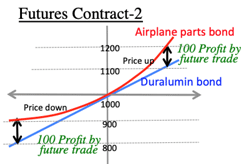
- >Top Future trade using Ito's lemma:
Case of airplane parts & duralumin:
camceling of the second term (volatility).
$\frac{dF}{dx}$ is called 'delta'.
|
