Intuitive Method of Physical Mathematics - Intuitive method of three-body problem and complex problem -	Cat: SCI Pub: 2011 #2007
	Shinichiro Naganuma (長沼伸一郎)	20510u

Title	Intuitive Method of Physical Mathematics	物理数学の直観的方法
Index	Preface: Mystery of three-body problem: Limit of Cartesian theory: The key to three-body problem: Faith in the harmonic universe: Impact on the modern medicine: Re-1: Determinant and eigenvalue: Total integration: :	序文: 三体問題の不思議: デカルト理論の限界: 三体問題への鍵: 調和的宇宙への信仰: 近代医学への影響: Re-1: 行列式と固有値: 全微分:
Tag	; Algebra-Analysis; Celestial mechanics; Christian world; Collapsar; Degeneration; Euler's identity; Rene Descartes; Diagonal matrix; Diagonalization; HGP; Individualism; Interaction matrix; Lagrangean point; Ernst Mach; Occam's razor; Pathogen; Professional group; Specialized differentiation; Taylor's expansion; Thinking economy; Three-body problem; Total differentiation;
Why	Basic thesis: 'the sum of the parts does not match the whole' - a new frontier of mathematics. Pursuing of Elaboration, Strictness, & Accuracy vs. Reviewing by Simplification, Synthesis, Intuition. Simplified knowledge understandable by university student can have the power to impact society. History of mathematics has been that of simplification; particularly simplified notation.

Original resume

Remarks

>Top 0. Preface: The author tried to explain mathematics in a style of too specialized from general readers and too simplified from specialists; such halfway explanation will be quite useful to grasp the landscape of some ten major topics of mathematics. The author tried not to write unnecessary explanation rather write necessary things. It is most interesting to read the author's lengthy postscript, where his essential point of claim is well described.

0. 序文: 内容は、一般読者には専門的過ぎ、専門家には簡略過ぎる中途半端のものがむしろ必要。 特に、やや長い後記の部分は、文明論にも言及している。以下その要約である。

>Top 1. Mystery of three-body problem: Two-body problem is soluble, but three-body problem is not. 300 years efforts since Newton's mechanics could not analytically solve the three-body problems, such as a problem of three mechanical effect of three celestial bodies of Sun, earth, and moon. Since those years, mathematics has remarkably developed including infinite space. Even the insoluble reason could not be proved; mathematics seems to avoid this sensitive three-body problem. This three-body problem was the first encountered 'complex problem' for mankind.; which gives us the best observation point to review the 300 years old problem and the present complex problem. 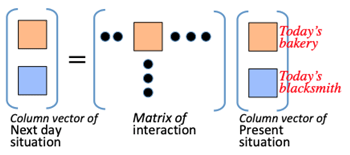Interaction of between groups: >Top First of all, consider the total image into segmented conceivable groups; i.e., society into professional groups. Second, watch daily interaction between the professional groups; total movement of the society can be expressed as the result of total interactions between all professional groups by matrix representation. (>Fig.) All interaction received by a particular professional (say: a bakery) is the sum of interactions from other groups. Next day's situation of all professional groups is represented by a vertical vector which is the same format of today's vertical vector. Third, $n$-th day's situation is expressed by multiplication $n$ times of such matrix. Factors other than professional groups: Social effects include additional interaction other than professional groups, which should be considered as revision factors. Such revision factors can be added by expanding the matrix size composed of the professional groups. 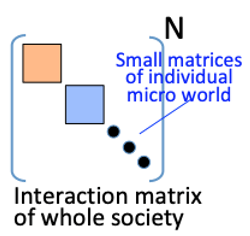>Top Interaction matrix: $\pmatrix{x(t)}=\pmatrix{A}^N\pmatrix{x_0}$; where $x_0$ is the initial state. $\pmatrix{A^{-1}}\pmatrix{A}^N\pmatrix{x_0}=\pmatrix{A}^{N-1}\pmatrix{x_0}$ $A^{-1}$ means backward one time to the past situation.

1. 三体問題の不思議: three-body problem: 三体問題 Three-body problem: (by Wikipedia) taking the initial positions and velocities (or momenta) of three point masses and solving subsequent motion according to Newton's laws of motion. (since 1687 published Principia) Three-body problem is a special case of the $n$-body problem, which describes how $n$ objects will move under mutual physical forces, such as gravity. $n$-body problem usually refers to a galaxy or to a cluster of galaxies, or planetary systems. Some applications are conveniently treated by perturbation theory, in which the system is considered as a two-body problem plus additional forces causing deviations from a hypothetical unperturbed two-body trajectory. Matrix of interaction:

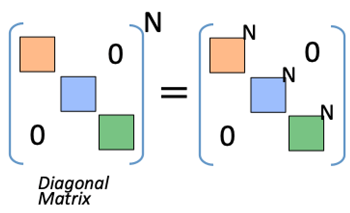
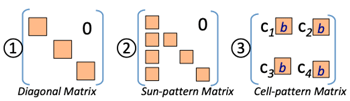
>Top 2. Limit of Cartesian theory: Limit of Cartesian Theory (=Analytical theory), which has been believed to be rational. Social expression is believed to be the sum of the divided components. That is, society is believed to be described as the total movements of all component groups (such as professional groups) Linear algebra shows $N-$th power of a diagonal matrix can be described: (>Fig.) this diagonal matrix can be decomposable into 2-by-2 determinant. (=two-body problem) In the solar system, gravity of the sun is outstanding; so the gravity of other satellites can be neglected. >Top Celestial mechanics: challenged to clarify the mechanics in the heaven where gods live; by which humans convinced the whole world could be expressed by analytic methods (illusion of harmonic cosmos).

2. デカルト理論の限界: Cartesian theory: デカルト理論 Diagonal matrix:

>Top 3. The key to three-body problem: Diagonalization: Solubility of a problem can be attributed to the possibility of such diagonalization of a determinant. 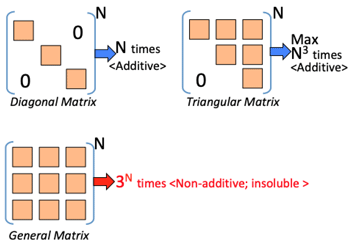Generally, any determinant has its own eigenvalue ($\lambda_{k}$) $A=P\Lambda P^{-1}$ $\Lambda=\begin{bmatrix}\lambda_{1}&&\\&\ddots&\\ &&\lambda_{k}\end{bmatrix}$ $A^N=P\underbrace{\Lambda P^{-1}･P\Lambda P^{-1}･\dots･P\Lambda}_{n\;\mathrm{times}} P^{-1}=P\Lambda^N P^{-1}$［n times multiplication］ where, there are two types of 'infinity': additive infinity (such as natural number, $N$ or rational number, $N^2$); and non-additive infinity (such as real number, $2^N$). Why two-body problem is soluble? 2-by-2 determinant can be converted to a triangle determinant by deleting only one element. (this means solubility) To convert a 3-by-3 determinant to a triangle determinant, at least three elements need to be deleted. (otherwise the calculation becomes insoluble due to 'mole-hitting effect'); or generally even deletion of two elements cannot be soluble. 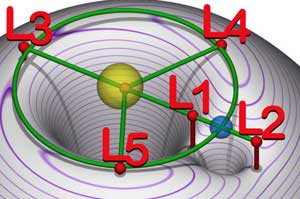>Top Lagrangean point: can be solved as 'equilibrium solution', which is an exceptional case; which is called a restricted three-body problem: there are 5 Lagrangean points: >Fig.

3. 三体問題への鍵: digonalization: 対角化 eigenvalue: 固有値 Additive or Non-additive: ・5 Lagrangean points: (wikipedia)

>Top 4. Faith in the harmonic universe: Three-body problem gives an impact to our civilization: now it became obvious that 'rationally solution' was actually exceptional cases; that is: 1) the portion of small matrices of interactions within the interaction matrix is all zero, or 2) interaction is outstanding from gigantic element (like gravity of the sun) and other interactions can be neglected, or 3) composed of similar small matrices like similar cells.: >Fig. 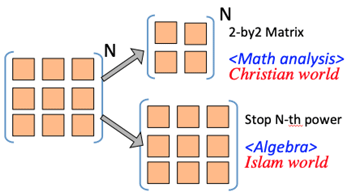>Top This idea has impacted on Christian world: Such 'pseudo' harmonious solution has affected to view of the Christian world.; because the celestial world has long believed being belonged to the god's sphere (unlike the view of Islamic world) >Top There are two pillars of development in mathematical history, such as: 1) mathematical analysis (composing of differential equations and functions, mostly deals with movement, and 2) algebra, mostly dealing many amounts ($x, y, ...$)

4. 調和的宇宙への信仰: algebra: <Ar. al-jabr, reunion of broken parts Soluble matrix: Christian world (Math Analysis) vs. Islam world (Algebra)

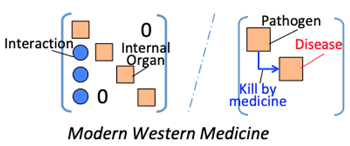
>Top 5. Impact on the modern medicine: The concept of pathogen was born with the modern Wester medicine; which means the disease will disappear by breaking the pathogen by medicine. (thus, medicine means diagnosis, treatment, and drug.) pathogen, drug, disease are divisible system. almost neglecting interactions between internal organs, or organ and bacteria/virus, etc. assuming a human body as a small harmonic cosmos. But actually, relationship of interactions should be more complicated, like spider's network. In Chinese medicine, the concept of pathogen is not obvious; explaining diseases come from the state of unbalanced situation of the body. A certain pathogen happens to exist the unbalanced portion, making the disease worse. This means that eradication of the pathogen does not always return to the complete cure. Side effects of medicine may be caused by unexpected ripple effect of interactions, because medicine cannot target to the affected area by the disease. >Top Individualism: Absolute freedom of individuals: This idea assumes that the society is an aggregation of individuals; maximization of individual right or profit will be the best situation. Mathematically, the sum of individual profit equals to (or, can be reduced) the society's profit. >Top Excessive specialized differentiation: Philosophers probably gave up to follow the logic of mathematics from a certain period; who feel some discomfort the contradiction between mathematics and real world, but who could not afford to debate it with mathematicians. 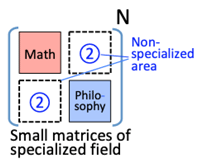While, mathematicians tend to stay in a narrow specialized area of the mathematics, having less interest to debate about wider social issues.: >Fig. Specialists feel it rather comfortable to live in a small specialized area. 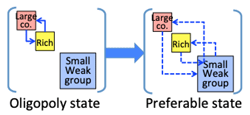Globalized Capitalism: Laissez-faire and Market Capitalism universalism entrusting God's invisible hand Causing meltdown of social order; expanding social disparity Oligopoly: turning around economy only within the wining group: It is a preferable state that the flow of money circulated passing all social components. >Fig. >Top There are more patterns of oligopolistic state than preferable state; which means the latter case could be substituted (or degenerated like a black hole) by the former from probability. Laisser-faire policy advocated by Adam Smith and his successors: They considered the concept of equilibrium, but did not that of degeneration or collapsar Thee-body problem of the solar system is solved considering that the sun's gravity is enormous, almost neglecting other gravities of satellites. Genetic engineering: >Top Human Genome Project (HGP) Reading of 3B of human genome does not mean to understand human genetic information at all. It should read 3B genome plus all interactions in a body; considering ecosystem and internal balance of the system, avoiding environmental destruction and degeneration by over simplification. >Top Occam's razor: William of Ockham (1287c-1347), scholastic philosopher <L. novacula Occami is a problem-solving principle, stating 'Entities should not be multiplied without necessity.' or, the simplest solution is most likely the right one; one should select the solution with the fewest assumptions. or, simpler theories are preferable to more complex ones because they are more testable. or Ptolemy (90-168): 'We consider it a good principle to explain the phenomena by the simplest hypothesis possible.' or 'It is vain to do with more what can be done with fewer.' >Top Ernst Mach (1838-1916): Austrian physicist and philosopher. criticized Newton' theories of space and time; foreshadowed Einstein's theory of relativity, but apparently rejected it. Mach defended a type of phenomenalism recognizing only sensations as real. he didn't believe the atoms exist!(1897); criticized by Max Planck as being incompatible with physics. his goal was the simplest and most economical abstract expression of facts. Machian physics: 'Phenomenological constructivism': should be based entirely on directly observable phenomena. should completely eschew absolute space and time in favor of relative motion. >Top Thinking economy: Theory-A can explain 20 phenomena, but it take 60 times efforts to understand the theory-A. Theory-B, a cheaper theory than theory-A, which can explain 10 phenomena, but it is easier to understand by only 5 time efforts. If there are two typed of theory-B, say theory-B1 and -B2, the sum of these can explain 20 phenomena with sum of efforts 10.; theory-B1 plus -B2 has the efficiency of understanding is sixth of theory-A. Is such division of theory-B really effective? this thought experiment implies fallacy of composition. It is needed to input an useful summary of knowledge in a limited capacity of our brain.

5. 近代医学への影響: pathogen: 病原体 <G. pathos, suffering regenerate: 縮退する falsibiability: 反証可能性 precursor: 先駆者 thinking economy: 思考経済 fallacy of compositon: 合成の誤謬 Premise of Western Medicine: Individual micro world: Small Specialized Area: Oligopoly state to Preferable state:

>Top 6. Re-1: Determinant and eigenvalue: eigenvalue (<G. eigen=proper, own, typical); named by Paul Dirac: Det $A=\pmatrix{1&{-\Delta}\\{-\Delta}&1}$ $Ax=\lambda x: \\\pmatrix{1&{-\Delta}\\{-\Delta}&1} \pmatrix{x\\y}=\lambda\pmatrix{x\\y}=\pmatrix{\lambda&0 \\0&\lambda}\pmatrix{x\\y}$ $\pmatrix{{1-\lambda}&{-\Delta}\\{-\Delta}&{1-\lambda}}\pmatrix{x\\y}=0 \longrightarrow\; \lambda_1=1+\Delta, \;\lambda_2=1+\Delta; $ $A=P\Lambda P^{-1}:\\ \longrightarrow \;P=\pmatrix{x_1&x_2\\y_1&y_2} =\pmatrix{1&1\\{-1}&1} , \; P^{-1}=\frac{1}{2}\pmatrix{1&{-1}\\1&1}$ $\pmatrix{\lambda&1\\0&\lambda}^n=\pmatrix{\lambda^n&n\lambda^{n-1}\\0&\lambda^n}$ [Jordan Normal Form] Geometrical meaning:

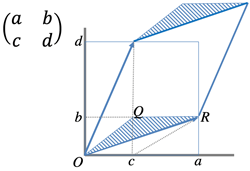
6. Re-1: 行列式と固有値: regular matrix (=invertible matrix): 正則行列 invertible matrix: 可逆行列 diagonal matrix (D)=対角行列 square matrix: 正方行列 symmetric matrix: 対称行列 transposed matrix: 転置行列 orthogonal matrix: 直交行列 upper triangle matrix: 上三角行列 transformation matrix: 変換行列 diagonalization: 対角化 matrix element: 行列の成分 non-trivial solution: 非自明解 rank: 階数 kernel (Ker): カーネル、核 rank-nullity theorem: 階数退化次数定理、次元定理 eigenvalue: 固有値 eigenvector: 固有ベクトル eigen equation: 固有方程式 eigenpolynomial: 固有多項式

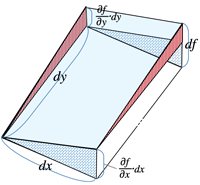
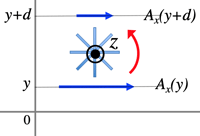
>Top ７. Total Differentiation: $\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy$ (>Fig.) $df$ can be integrated along the integration path $C$ on $x-y$ plane.

7. 全微分: Total differentiation:

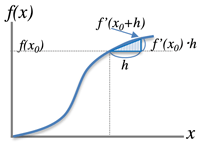
>Top 8. Taylor Expansion: $f(x_0+h)=f(x_0)+\frac{f'(x_0)}{1!}h+\frac{f''(x_0)}{2!}h^2 +\frac{f'''(x_0)}{3!}h^3+\dots$ $\dfrac{f(x_0+h)-f(x_0)}{h}=f'(x_0)\;$ [definition of $f'(x_0)$]

8. テイラー展開: Taylor Expansion:

>Top 9. Image of Euler's identity: $e^{i\theta}=\cos{\theta}+i\sin{\theta}$ Exponential derivative: $\frac{d}{dx}(a^x)=\displaystyle\lim_{d\to 0}\frac{a^{x+d}-a^x}{d} =\displaystyle\lim_{x\to 0}a^x\left(\frac{a^d-1}{d}\right) $ here: $\frac{a^d-1}{d}=1$ $e=\displaystyle\lim_{d\to 0}(1+d)^{\frac{1}{d}}\;$ where, [$a\rightarrow e \;\; (d\rightarrow 0)$] Cf: Unit of multiplication is $1$, while unit of addition is $0$. 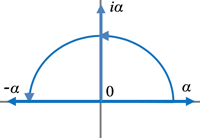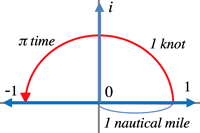Image of $e$ and $i$: $e$ is derived from differential calculation, and $i$ from squared. $e^{it}$ (Traditional navigation could not know directly its sailing longitude.) $e^0=1$ is the starting point, and its first differential is $\alpha e^{\alpha t}$; the speed increases as moving away from the origin. Position vector $e^{i\alpha t}$; velocity vector $i\alpha e^{i\alpha t}$, which is always perpendicular to the position vector; whose course is unit circle. $\therefore e^{i\pi}=-1$

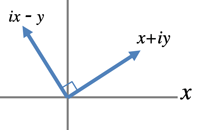
9. xxxx: Conjugate complex number: Sailing along the unit circle:

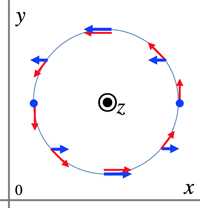
>Top 10. Vector Analysis: gra (=gradient): grad $\phi(x,y,z)\equiv \nabla\phi=\pmatrix{\frac{\partial\phi}{\partial x}\\ \frac{\partial\phi}{\partial y}\\\frac{\partial\phi}{\partial z}}$ div (=divergence) vector: div $A(x,y,z)\equiv \nabla･A=\frac{\partial A_x}{\partial x} +\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}$ rot (=rotation) is the operator to represent a vertex in a vector field (e.g., elctromagnetic field) $rot E\equiv\nabla\times A=\pmatrix{{\frac{\partial E_z}{\partial y}-\frac{\partial E_y}{\partial z}}\\ \frac{\partial E_x}{\partial z}-\frac{\partial E_z}{\partial x}\\ \frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}} $ Turning power: $\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\;$ [minus means counterclockwise turning force]

10. ベクトル解析: rot =rotation vortex:

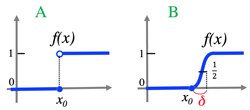
>Top 10. $\epsilon -\delta$ reasoning: Proof of equality: prove $a=b$ directly prove $a=c$ and $b=c$, then $a=b$ prove $a\le b$ and $a\ge b$, then $a=b$ where $|a_n-b|<c_n$: when $c_n\rightarrow 0$, then $|a_n-b| \rightarrow 0$, that is, $a_n=b$ , finally $a=b\;$ [point sequence] Continuity: $^{\forall}\varepsilon>0,^{\exists}\delta>0$ s.t.$^{\forall} x\in\mathbb{R}, |x-a|<\delta \Rightarrow |f(x)-f(a)|<\varepsilon$ Continuous/Discontinuous function: (>Fig.) Here, if any $\varepsilon$ is $\frac{1}{2}$, then $\delta$ can be selected as in the figure B, then $^{\exists}\delta$ such that $|f(x)-f(x_0)|<\frac{1}{2}$ But, in the figure A, if any $^{\forall}\varepsilon>0, then ^{\nexists}\delta>|x-x_0|$ s.t.$\Rightarrow |f(x)-f(x_0)|<\varepsilon$. Thus, modern algebra uses lots of inequality.

10. xxxx: s.t.: such that

>Top 10. Imaxxxxx: $e^{i\theta}=$

10. xxxx:

>Top 10. Imaxxxxx: $e^{i\theta}=$

10. xxxx:

>Top 10. Imaxxxxx: $e^{i\theta}=$

10. xxxx:

Comment

It needs creativity to simply describe difficult issue. This book reminds us the needs of cross-cultural education. Response to the Covid-19 issue should be comprehensive than fragmentary, and this book is on-target petinent.

難しい問題を簡単に記述することには創意工夫がいる。 本来の教養とは何かを考えさせてくれる良書である。 ウイルスへの対応も断片的ではなく総合的にすべきであり、本書の指摘は正鵠を得ている。