Mathematics to understand Deep Learning	Category: ICT Published: 2017 #1711b
	Yoshiyuki & Sadami Wakui (涌井良幸･貞美)	up 17810

Title	Mathematics to understand Deep Learning	ディープラーニングがわかる数学
Index	Introduction: How to express activity of neuron: How the neural network learns: Basic mathematics for neural network: Cost function of neural network: Back propagation method: Translation to neural network language:	序文: ニューロンの働きの表現: ニューラルネットワークはどう学ぶのか: ニューラルネットワークのための基本数学: ニューラルネットワークのコスト関数: 誤差逆伝搬法 (BP法): ニューラルネットワークの言葉に翻訳:
Tag	; Axon; Back propagation method; Chain rule; Convolution layer; Cost function; Data dependent; Dendrite; Demon-Subordinate Network; Displacement vector; Gradient descent; Lagrange multiplier method; Learning data; Minimization problem; Neural network; Neurotransmission; Recurrence formula; Regression analysis; Sigmoid function; Similarity of pattern; Square error; Stress tensor; Synapse;

Résumé	Remarks
>Top 0. Introduction: Activity of Neuron:	0. 序文: ニューロンの働き

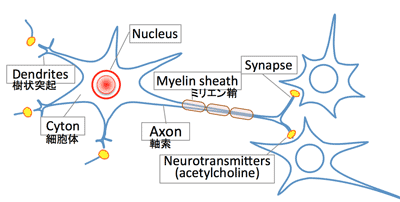
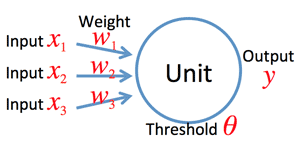
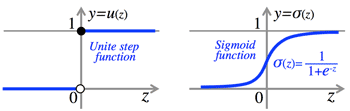
>Top 1. How to express activity of neuron: Neuron is composed of: Cyton: cell body (=neuron) Dendrites: Input of information Axon: Output of information >Top Unit step function vs. Sigmoid function (differentiable): Unite step function: Output is 0 or 1. Sigmoid function ($\sigma (z)=\frac{1}{1+e^{-z}}$): Output is arbitrary number. 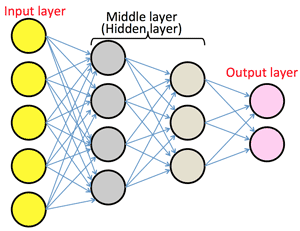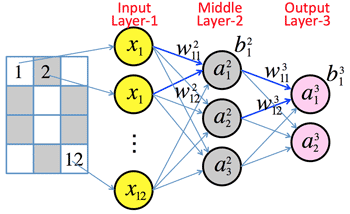Activation function: $y=a(w_1x_1+w_2x_2+w_3x_3-\theta)\; (\theta: $threshold) >Top Neural Network: (>Fig.) Input layer - Middle layer - Output layer: Input layer: no input arrows; output only. Middle (Hidden) layer: actually process the information this layer reflects intention of the planner. 'hidden demons' in the middle layer have particular properties, which are different sensitivity of a specific pattern. Output layer: output as the total of neural network. Deep Learning: neural network having many deep layers. Fully connected layer: All units of the previous layer point to the next layer. 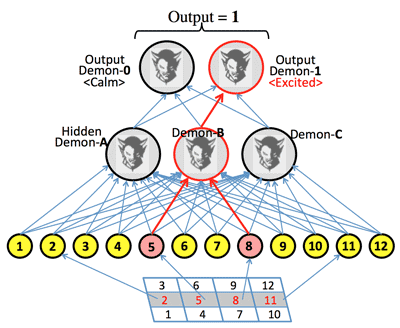>Top Compatibility of Demons and their subordinates: (>Fig) Pixel 5 & 8 ON Subordinate 5 & 8 excited Hidden Demon-B excited Output Demon-1 excited The picture was judged to be "1". Thus, compatibility or bias of each Demon leads the answer; The network decides as a whole. >Top AI Development phases: Gen. Period Key App. 1G 1950s-60s Logic dependent Puzzle 2G 1980s Knowledge dependent Robot; Machine translation 3G 2010- Data dependent Pattern recog; Speech recog.

1. ニューロンの働きの表現: Neurotransmission (神経伝達): Input $z$は、以下２ベクトルの内積: $z=(w_1,w_2,w3,b)(x_1,x_2,x_3,1)$ Neural Network: Demons and their subordinates: Subordinates reflect vividly 4 & 7, and 6 & 9. 1 2 3 4 5 6 7 8 9 10 11 12 Demon-Subordinate Network:

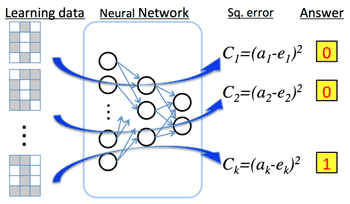
>Top 2. How the neural network learns: >Top Regression Analysis: Learning with teacher or without teacher: (>Fig.) With teacher: Learning data (or Supervised data) To minimize the errors between estimate and correct answer; 'Least-square method'; 'Regression Analysis' Total of errors: cost function $C_T$ Weight parameter can take negative value, unlike the case of biology.

2. ニューラルネットワークはどう学ぶのか: Regression Analysis (回帰分析):

>Top 3. Basic mathematics for neural network: Inner products: $a･b=|a||b|\cos\theta$ Cauthy-Schwarz inequality: $-|a||b|\le a･b\le |a||b|$ $-|a||b|\le |a||b|\cos\theta\le |a||b|$ Similarity of pattern: $A =\pmatrix{x_{11}&x_{12}&x_{13} \cr x_{21}&x_{22}&x_{23} \cr x_{31}&x_{32}&x_{33}}$ $F =\pmatrix{w_{11}&w_{12}&w_{13} \cr w_{21}&w_{22}&w_{23} \cr w_{31}&w_{32}&w_{33}}$ Similarity=$A･F=w_{11}x_{11}+w_{12}x_{12}+...+w_{33}x_{33}$ Similarity is proportional to the Inner product of A and F. 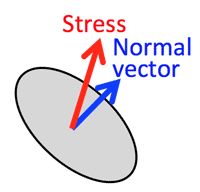Stress tensor: (>Fig.) Stress tensor ($T)=\pmatrix{\tau_{11}&\tau_{12}&\tau_{13} \cr \tau_{21}&\tau_{22}&\tau_{23} \cr \tau_{31}&\tau_{32}&\tau_{33}}$ Google: 'Tensor-Flow' Matrix product: $AB=\pmatrix{c_{11}&c_{12}&\ldots&c_{1p} \cr c_{21}&c_{22}&\ldots&c_{2p} \cr \vdots&\vdots&\ddots&\vdots\cr c_{n1}&c_{n2}&\ldots&c_{np}}=c_{ij}=\displaystyle\sum_{k=1}^m a_{ik}b_{kj}$ Hadamard product: $A\circ B=\biggl(a_{ij}･b_{ij}\biggr)_{1\le i\le m\\1\le j\le n}$ Transposed matrix: $^tB\:^tA$ (>¶) >Top Differential: (Composite function = Chain rule) $\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$ $\frac{\partial z}{\partial x} =\frac{\partial z}{\partial u}\frac{\partial u}{\partial x} +\frac{\partial z}{\partial v}\frac{\partial v}{\partial x} $ $\frac{\partial z}{\partial y} =\frac{\partial z}{\partial u}\frac{\partial u}{\partial y} +\frac{\partial z}{\partial v}\frac{\partial v}{\partial y} $ $(e^{-x})^{'}=-e^{-x}$ $y=e^u, \; u=-x:$ then, $y^{'}=\frac{dy}{du}\frac{du}{dx}=d^u･(-1)=-e^{-x}$ $\frac{1}{f(x)}^{'}=-\frac{f^{'}(x)}{\{f(x)\}^2}$ $\sigma (x)=\frac{1}{1+e^{-x}}$ (Sigmoid function) $\sigma^{'}(x)=\sigma(x)(1-\sigma(x))$ (>¶) Multivariable function: Partial differential (derivative): $\frac{\partial z}{\partial x}=\frac{\partial f(x,y)}{\partial x}$ $\displaystyle\lim_{\Delta x\to 0}\frac{f(x+\Delta x, y)-f(x,y)}{\Delta x}$ $\frac{\partial z}{\partial y}=\frac{\partial f(x,y)}{\partial y}$ $\displaystyle\lim_{\Delta y\to 0}\frac{f(x, y+\Delta y)-f(x,y)}{\Delta y}$ >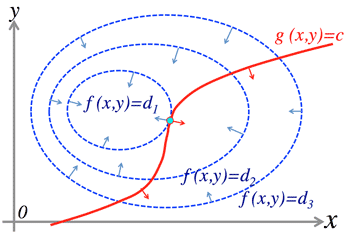Top Lagrange multiplier method: Finding local maxima and minima of a function subject to equality constraints. Maximize $f(x,y)\; $ subject to $g(x,y)=0$ $F(x,y,\lambda)=f(x,y)-\lambda(g(x,y)-c)$ $\frac{\partial F}{\partial x} =\frac{\partial F}{\partial y} =\frac{\partial F}{\partial \lambda}=0$ Approximate formula: $f(x+\Delta x)\approx f(x)+f^{'}(x)\Delta x$ $f(x+\Delta x, y+\Delta y)\approx f(x,y)+ \frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y$ $\Delta z\approx \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y$ $\Delta z\approx \frac{\partial z}{\partial w}\Delta w + \frac{\partial z}{\partial x}\Delta x + \frac{\partial z}{\partial y}\Delta y$ $\nabla z=(\frac{\partial z}{\partial w}, \frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}), $ $\Delta x=(\Delta w, \Delta x, \Delta y) $ >Top Gradient descent: (>Fig.) $\Delta z=\frac{\partial f(x,y)}{\partial x}\Delta x + \frac{\partial f(x,y)}{\partial y}\Delta y$ When $\Delta z$ becomes minimum: two vectors are in the opposite direction. $(\Delta x, \Delta y)=-\eta (\frac{\partial f(x,y)}{\partial x} ,\frac{\partial f(x,y)}{\partial y})$ $\Delta x=(\Delta x_1, \Delta x_2, ..., \Delta x_n)= -\eta\nabla f \;$, where $\Delta x$ is a displacement vector; $\eta$ is a small positive number; $\nabla f=(\frac{\partial f}{\partial x_1} ,\frac{\partial f}{\partial x_2}, ... , \frac{\partial f}{\partial x_n })$

3. ニューラルネットワークのための基本数学: Stress tensor: 転置行列: ¶ $A=\pmatrix{a_{11}&\ldots&a_{1n}\cr \vdots&&\vdots\cr a_{m1}&\ldots&a_{mn}}$ $B=\pmatrix{b_{11}&\ldots&b_{1p}\cr \vdots&&\vdots\cr b_{n1}&\ldots&a_{np}}$ $(i, j)$ element of $AB \; (=(j,i)$ element of $^t(AB))$: $\pmatrix{a_{i1}&a_{i2}&\ldots&a_{1n}} \pmatrix{b_{1j}\cr b_{2j}\cr \vdots\cr b_{nj}}$ $ =\displaystyle\sum_{k=1}^na_{ik} b_{kj}$ $(j,i)$ element of $ ^tB\: ^tA$: $\pmatrix{b_{j1}&b_{j2}&\ldots&b_{nj}} \pmatrix{a_{i1}\cr b_{i2}\cr \vdots\cr b_{in}}$ $ =\displaystyle\sum_{k=1}^nb_{kj} a_{ik} =\displaystyle\sum_{k=1}^na_{ik}b_{kj}$ $\therefore \; ^t(AB)=$ $^tB\:^tA$ ¶ $\sigma^{'}(x) =-\frac{1+e^{-x}}{(1+e^{-x})^2} =\frac{e^{-x}}{(1+e^{-x})^2} =\frac{1+e^{-x}-1}{(1+e^{-x})^2}$ $=\frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x})^2} \sigma(x)-\sigma(x)^2 =$ Lagrange Multiplier (ラグランジュ未定乗数法): Blue lines are counturs of $f(x,y)$ Red line shows the constraint $g(x,y)=c$ 勾配降下法 (Gradient descent method) 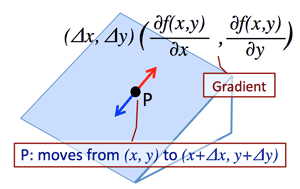Displacement vector (変位ベクトル) ¶ $z=x^2+y^2; \Delta x=-\eta\nabla z=(2x, 2y)$

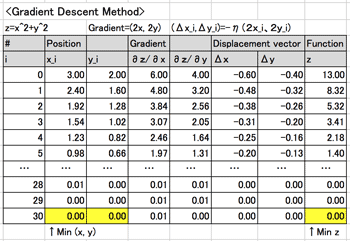
>Top 4. Cost function of neural network: Gradient Descent (Sample): (>Fig.) <Middle layer> $\pmatrix{z_1^2\cr. z_2^2\cr. z_3^2} =\pmatrix{w_{11}^2&w_{12}^2&w_{13}^2&\ldots&w_{112}^2\cr. w_{21}^2&w_{22}^2&w_{23}^2&\ldots&w_{212}^2\cr. w_{31}^2&w_{32}^2&w_{33}^2&\ldots&w_{312}^2} \pmatrix{x_1\cr. x_2\cr. x_3\cr.\ldots\cr. x_{12}} +\pmatrix{b_1^2\cr. b_2^2\cr. b_3^2} $ $a_i^2=a(z_i^2)\; (i=1, 2, 3)$ <Output layer> $\pmatrix{z_1^3\cr. z_2^3} =\pmatrix{w_{11}^3&w_{12}^3&w_{13}^3&\cr. w_{21}^3&w_{22}^3&w_{23}^3} \pmatrix{a_1^2\cr. a_2^2\cr. a_3^2} +\pmatrix{b_1^3\cr. b_2^3} $ $a_i^3=a(z_i^3)\; (i=1, 2)$ <C=Square error> $C=\frac{1}{2}\{(t_1-a_1^3)^2+(t_2-a_2^3)^2\}$ <$C_T$=Cost function> $C_T=\displaystyle\sum_k^{64} C_k$ $C_k=\displaystyle\sum_k^{64} C_k\frac{1}{2}\{(t_1[k]-a_1^3[k])^2+(t_2[k]-a_2^3[k])^2\}$ Applying Displacement Descent: $\Delta x=(\Delta x_1, \Delta x_2, ..., \Delta x_n)= -\eta\nabla f \; $ (where $\nabla f$ is Gradient) $(\Delta w_{11}^2,\ldots,\Delta w_{11}^3,\ldots ,\Delta b_1^2,\ldots,\Delta b_1^3,\ldots) $ $=-\eta \Bigl(\frac{\partial C_T}{\partial w_{11}^2} ,\ldots,\frac{\partial C_T}{\partial w_{11}^3} ,\ldots,\frac{\partial C_T}{\partial b_1^2} ,\ldots,\frac{\partial C_T}{\partial b_1^3},\ldots\Bigr)$

4. ニューラルネットワークのコスト関数: 勾配降下法 (例):

>Top 5. Back propagation method: Square error; Minimization problem of Cost function: $C=\frac{1}{2}\{(t_1-a_1^3)^2+(t_2-1_2^3)^2\}$ $\delta_j^l=\frac{\partial C}{\partial z_j^l}\; (l=2, 3, \ldots)$ $\frac{\partial C}{\partial w_{11}^2} = $\frac{\partial C}{\partial z_1}^2} {\partial z_1^2}{\partial w_{11}^2} $z_1^2=w_{11}^2x_1+w_{12}^2x_2+\ldots +w_{112}^2x_{12}+b_1^2$ $\frac{\partial C}{\partial w_{11}^2}=\delta_1^2x_1 =\delta_1^2a_1^1$ >Top <General formula>: from partial differentail to recurrence formula. 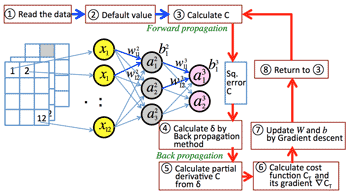$\frac{\partial C}{\partial w_{ji}^l}=\delta_j^la_i^{l-1}$ $\frac{\partial C}{\partial b_j^l}=\delta_j^l$ Forward & Back Propagation: <Forward Propagation> Read the data. Set up the default data. Calculate $C$. Square error $C$. <Back Propagation> Calculate $\delta$ by Back propagation method. Calculate Cost function $C_T$ and its gradient $\nabla C_T$. Update Weight $W$ ana bias $b$ by Gradient descent method. Return to 3. <Matrix representation> $\pmatrix{\delta_1^3\cr \delta_2^3} =\pmatrix{\frac{\partial C}{\partial a_1^3}\cr \frac{\partial C}{\partial a_2^3}} \circ \pmatrix{a^{'}(z_1^3)\cr a^{'}(z_2^3)}$ $\pmatrix{\delta_1^2\cr \delta_2^2\cr \delta_3^2} =\Biggl[\pmatrix{w_{11}^3& w_{21}^3\cr w_{12}^3& w_{22}^3\cr w_{13}^3& w_{23}^3 }\pmatrix{\delta_1^3\cr \delta_2^3}\Biggr] \circ \pmatrix{a^{'}(z_1^2)\cr a^{'}(z_2^2)\cr a{'}(z_3^2}$

5. 誤差逆伝搬法 (BP法): $C$: 二乗誤差 $\delta_j^l$: Unitの誤差の定義 <コスト関数$C_T$の最小化問題> 最小条件の方程式 $\frac{\partial C_T}{\partial x}=0, \frac{\partial C_T}{\partial y}=0, \frac{\partial C_T}{\partial z}=0$ 勾配降下法: 勾配$(\frac{\partial C_T}{\partial x}, \frac{\partial C_T}{\partial y}, \frac{\partial C_T}{\partial z})$ 誤差逆伝搬法: Solved partial differential value by recurrence formula. Forward propagation & Back propagation:

>Top 6. Translation to neural network language: Favorite pattern of a demon: Gradient of Cost function $C_T$ >Top Convolution layers: $=(\frac{\partial C_T}{\partial w_{11}^{F1}}, \ldots, \frac{\partial C_T}{\partial w_{1-11}^{01}}, \ldots, \frac{\partial C_T}{\partial b^{F1}}, \ldots, \frac{\partial C_T}{\partial b_{1}^{0}}, \ldots, )$ 1st term: Partial differential of filter. 2nd term: Partial differential of unit weight of output layer. 3rd term: Partial differential of unit weight of 'convolution' layers. 4th term: Partial differential of unit weight of output layer.

6. ニューラルネットワークの言葉に翻訳: Feature Map by convolution of Filter-S: 2 1 0 1 0 0 1 2 0 0 3 0 0 3 1 1   Convolution layers (畳み込み層): Picture >Similarity >Convolution (Weight) >Convolution (Output) >Pooling:

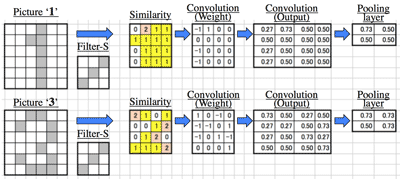
Comment

Mathematics for deep learning relates mostly partial differential. Recurrence formula are easier for computer to calculate than partial differentials, and are used instead. It is interesting to understand how AI understand analog picture to digitized recognition, by doing complicated mathematical calculations. It is as expected that computing ability in quick calculation is a decisive factor. Computer itself is no more smart but is only speedy in calculation.

ディープラーニングの数学は、特に偏微分に関連する。コンピュータにとっては、偏微分より漸化式の法が得意なのでよく代用される。 AIが複雑な数学計算によって、どのようにアナログな図をデジタル認識するのかは興味深い。それにしても予想通り、コンピュータの計算力の早さが決め手である。 コンピュータ自体がスマートという訳ではなく、単に計算が速いだけなのである。