>Note	Bitcoin: A Peer-to-Peer Electronic Cash System	Cat: ICT Pub: 2009/5 #: 1613b
		Satoshi Nakamoto, etc.	16626u/18802r

Title	Bitcoin: A Peer-to-Peer Electronic Cash System	ビットコイン: P2P電子マネーシステム
Index	Abstract: Introduction: Transactions: Time Stamp Server: Proof of Work: Network: Incentive: Reclaiming Disk Space: Simplified Payment Verification: Combining and Spritting Value: Privacy: Calculations: Conclusions: PS-1: PS-2:	要旨: 序文: 取引: 時刻認証サーバ: プルーフオブワーク: ネットワーク: インセンティブ: ディスク空間の再利用: 簡便な支払認証: 価値の合算と分割: プライバシィ: 計算: 結論: 補足1: 補足2:
Tag	; 51% Attack; Authenticity; Block; Byzantine Generals Problem; Consensum algorithm; Ethereum; Genesys block; Hard fork; Hashcash; Hashpower; Hyperledger Fabric; Longest chain; Multi-signiture; Nonce; Non-reversible transaction; Parallel chain; PBFT; POH: POI; POS: Proof-of-work (POW); Ripple; SHA-256; Timestamp server; Usenet; UTXO; Wallet;

Résumé

Remarks

>Top 0. Abstract: A purely peer-to-peer version of electronic cash would allow online payments to be sent directly from one party to another without going through a financial institution. Digital signatures provide part of the solution, but the main benefits are lost if a trusted third party is still required to prevent double-spending. >Top We propose a solution to the double-spending problem using a peer-to-peer network. The network timestamps transactions by hashing them into an ongoing chain of hash-based proof-of-work, forming a record that cannot be changed without redoing the proof-of-work. The longest chain not only serves as proof of the sequence of events witnessed, but proof that it came from the largest pool of CPU power. As long as a majority of CPU power is controlled by nodes that are not cooperating to attack the network, they'll generate the longest chain and outpace attackers. The network itself requires minimal structure. Messages are broadcast on a best effort basis, and nodes can leave and rejoin the network at will, accepting the longest proof-of-work chain as proof of what happened while they were gone.

0. 要旨: 真の電子マネーのP2P版は一方の当事者から他の当事者は金融機関を通さずに直接送金できる。 デジタル署名はその解決方法となるが、信用できる第三者が二重支払の防止を要求するとすれば、主な利便性は失われる。 そこでP2Pネットワークを利用して二重支払の問題の解決を提案する。取引データをハッシュ化しネットワークの時刻認証をすることで、ハッシュベースPOW (Proof of Work)チェーンを継続することで、POWをやり直し無しには取引記録を変更できない。 最長のチェーンは継続的な取引の証明であるだけでなく、CPUパワーの最大容量からの証明ともなる。 多数のCPUパワーによってノードが管理されていれば、ネットワーク攻撃への協力はできない。その結果最長チェーンを生成し、攻撃者を凌駕できる。 ネットワーク自体は最小の構造からなる。取引通知はベストエフォットベースでブロードキャストされ、またノードは任意にネットワークから離れたり参加でき、離脱中は最長のPOWチェーンを選択することでその間の取引証明とする。

>Top 1. Introduction: >Top Commerce on the Internet has come to rely almost exclusively on financial institutions serving as trusted third parties to process electronic payments. While the system works well enough for most transactions, it still suffers from the inherent weaknesses of the trust based model. Completely non-reversible transactions are not really possible, since financial institutions cannot avoid mediating disputes. The cost of mediation increases transaction costs, limiting the minimum practical transaction size and cutting off the possibility for small casual transactions, and there is a broader cost in the loss of ability to make non-reversible payments for non-reversible services. With the possibility of reversal, the need for trust spreads. Merchants must be wary of their customers, hassling them for more information than they would otherwise need. A certain percentage of fraud is accepted as unavoidable. These costs and payment uncertainties can be avoided in person by using physical currency, but no mechanism exists to make payments over a communications channel without a trusted party. What is needed is an electronic payment system based on cryptographic proof instead of trust, allowing any two willing parties to transact directly with each other without the need for a trusted third party. Transactions that are computationally impractical to reverse would protect sellers from fraud, and routine escrow mechanisms could easily be implemented to protect buyers. In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions. The system is secure as long as honest nodes collectively control more CPU power than any cooperating group of attacker nodes.

1. 序文: インターネット上の商取引は、ほとんどすべて電子決済プロセスに対する信頼できる第三者としての金融機関に依存している。ほとんどの取引でシステムが順調に機能している一方では、この信頼ベースモデルには本来的な弱点が存在する。完全に取消不能な取引は可能ではない、というのは金融機関は紛争の仲介を避けることができないからである。 仲介費用は取引コストを増加させ、実際の取引規模を最小に制限し、偶発的な取引の可能性を遮断する。また取消不能なサービスに対する取消不能な支払能力のためのロスも大きなコストとなる。取消の可能性によって信頼に関わるニーズが拡大する。業者はその顧客にうんざりし、別のニーズを求める以上の多くの情報が必要となることに悩まされるようになる。 一定程度の詐欺行為は不可避である。これらのコストや支払不確実は現物決済によって個別に回避できるが、信頼できる当事者なしにコミュニケーションチャネルに対して支払うメカニズムは存在しない。 電子決済システムに必要なものは信頼の代わりに暗号による証明であり、これによって意思のある当時者は信頼できる第三者を必要とせずに相互に直接取引することを可能にする。取引を取り消すことが計算上不可能であることから売り主を詐欺から保護でき、買い主を保護するには通常のエスクロメカニズムを容易に導入できる。 本論文では、P2Pの分散時刻認証サーバを利用して取引の時系列の計算上の証明を行うことで二重支払の問題を解決することを提案する。このシステムはCPU能力において、ノードを攻撃するグループよりも信頼できる能力が全体として勝っていれば安全となる。

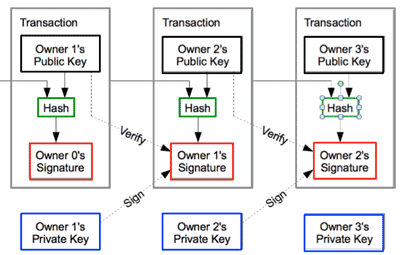
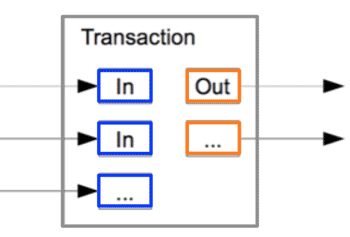
>Top 2. Transactions: We define an electronic coin as a chain of digital signatures. Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin. A payee can verify the signatures to verify the chain of ownership. <Fig.2> The problem of course is the payee can't verify that one of the owners did not double-spend the coin. A common solution is to introduce a trusted central authority, or mint, that checks every transaction for double spending. After each transaction, the coin must be returned to the mint to issue a new coin, and only coins issued directly from the mint are trusted not to be double-spent. The problem with this solution is that the fate of the entire money system depends on the company running the mint, with every transaction having to go through them, just like a bank. We need a way for the payee to know that the previous owners did not sign any earlier transactions. For our purposes, the earliest transaction is the one that counts, so we don't care about later attempts to double-spend. The only way to confirm the absence of a transaction is to be aware of all transactions. In the mint based model, the mint was aware of all transactions and decided which arrived first. To accomplish this without a trusted party, transactions must be publicly announced [1], and we need a system for participants to agree on a single history of the order in which they were received. The payee needs proof that at the time of each transaction, the majority of nodes agreed it was the first received.

2. 取引: 我々は電子コインをデジタル署名のチェーンとして定義する。各々の所有者が自身のコインを振替するには、それ迄の取引のハッシュにデジタル署名して、かつ次の所有者の公開鍵を当該コインの末尾に追加する。受取人は署名認証することで、そのチェーンの所有者を認証する。 もちろん問題は受取人は二重支払のコインの所有者かどうかまでは認証できない。通常の解決は信頼できる中央権威者、即ち貨幣発行者を導入し、当該コインは発行者に戻して新コインを発行することである。発行者から直接発行されたコインは信頼でき、二重支払ではない。この解決の問題点は、全て貨幣システムの運命は貨幣発行者に依存していることであって、すべての取引が、銀行のような組織を通じなければならないことである。 受取人にとってそれ以前の所有者が以前の取引について証明しなかったことを知る方法が必要となる。そのためには、それまでの取引が計算できることが必要で、その後の二重支払の可能性は関係ない。 取引がないことを確認する唯一の方法は全ての取引を知ることである。貨幣発行者ベースのモデルでは、貨幣発行者は全ての取引を知っており最初に発生した取引を決定できる。これを信頼できる第三者なしに行うには、取引が公開通知され、取引参加者は彼らが受け取る一連の取引に合意する必要がある。受取人は、取引の都度多数のノードが最初に受領したことに合意していることを認証する必要がある。

<Fig.2> Sigining a hash of the previous transaction:

<Fig.3> Timestamp Server:

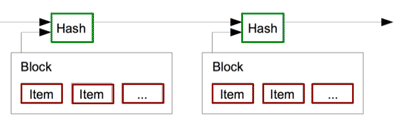
>Top 3. Time Stamp Server: The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post [2-5]. The timestamp proves that the data must have existed at the time, obviously, in order to get into the hash. Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it. Timestamp records when the Blockchain is made; using by the UNIX Time (UTC); in term of seconds started from 00.00.00 on Jan. 1, 1970. Bitcoin started from 3/Jan./2009, as shown in the first block of Genesys Block.

3. 時刻認証サーバ: 時刻認証サーバを導入することで解決する。時刻認証サーバは時刻認証すべき一連の項目をハッシュ化する、そのハッシュ化はニュースあるいはUsernetで配信することで公開される。この時刻認証はハッシュ化することで当該データがその時点で存在していることを証明する。各々の時刻認証はそれ以前の時刻認証を含めてハッシュ化し、チェーンを作成し、追加の時刻認証することでそれ以前のチェーンを強化する。 タイムタンプは、ブロックチェーンが作成された時間を、UNIX時間、即ち1970年1月1日00:00:00からの経過秒数で記録される。 ビットコインは、2009年1月3日から開始された。(最初のブロックであるジェネシスブロックの記述)

* 注) Hash function: 要約函数; データが与えられた時、そのデータを代表する数値(ハッシュ値)を得る操作。検索の高速化、データ比較、改竄の検出、重複データの検出等に利用される。 Hashcash: 1997年にAdam Backが提案したPOWシステムで一定量の計算をさせることで効率的にDOS攻撃などを防ぐことができる。 SHA-2 (Secure Hash Algorithm 2): 米国NSAが設計した暗号ハッシュ機能のセットである。Bitcoinでは、SHA-256 (256bit, 32byte)とRIPEMO-160 (160bit, 20byte)のハッシュ関数がアドレスや取引情報に利用されている。但し、出力桁数は固定で16進数で表記される。 Block chain: ビットコインの全取引履歴 Nonce: 暗号通信で利用する使い捨てのランダム値。これによってリプレイ攻撃を阻止する。Nonceに書き込むデータによってそのblockのハッシュ値を変化させ、決められた値(Difficulty target)より小さくなったらBlockが完成する。これにはコンピュータの高い処理能力を必要とする。 Hash tree; Merkle tree (マークル木); より大きなデータの要約結果を格納する木構造の一種でデータの検証に利用される。 Fan-out/Fan-in: 論理回路における論理出力数と論理入力数 Proof of Work (POW): 条件を満たしたBlockが一番大奥つながっているBlockが、正規のものとみなされる。この仕事量をPOWという。 Alternate Coin (Alt-Coin): Bitcoinの後に作られた仮想通貨のこと。現在700種類以上あると言われる。

>Top 4. Proof of Work: To implement a distributed timestamp server on a peer-to-peer basis, we will need to use a proof-of-work system similar to Adam Back's Hashcash [6], rather than newspaper or Usenet posts. The proof-of-work involves scanning for a value that when hashed, such as with SHA-256, the hash begins with a number of zero bits. The average work required is exponential in the number of zero bits required and can be verified by executing a single hash. For our timestamp network, we implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block's hash the required zero bits. Once the CPU effort has been expended to make it satisfy the proof-of-work, the block cannot be changed without redoing the work. As later blocks are chained after it, the work to change the block would include redoing all the blocks after it. The proof-of-work also solves the problem of determining representation in majority decision making. If the majority were based on one-IP-address-one-vote, it could be subverted by anyone able to allocate many IPs. >Top Proof-of-work is essentially one-CPU-one-vote. The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains. To modify a past block, an attacker would have to redo the proof-of-work of the block and all blocks after it and then catch up with and surpass the work of the honest nodes. We will show later that the probability of a slower attacker catching up diminishes exponentially as subsequent blocks are added. To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they're generated too fast, the difficulty increases.

4. プルーフオブワーク (仕事量による証明): 分散時刻認証サーバをP2Pベースで構築するためには、ニュースやユーズネット配信よりも、Adam BackのHashcashの仕組みに似たPOWシステムを利用する必要がある。 POWはハッシュ化する際には、SHA-256のような方式を使い、ハッシュは要求されるゼロビットの数字から始まる。このゼロビット数が増えると仕事量は冪乗で増加し、単一のハッシュを実施することで認証されることができる。 我々の時刻認証ネットワークは、POWをブロックにランダム値(nonce)を増加することで、要求されたゼロビットのブロックをハッシュ化するのに必要な数値まで増加させるように規定する。一旦CPUの努力でPOWを満足させるように消費されると、そのブロックは作業をやり直しをしなければ変更されない。その後のブロックは最後尾にチェーンされるので、そのブロックを変更する作業はその後の全てのブロックをやり直しをしなければならなくなる。 POWはまた多数による意思決定による表示を決めるという問題を解決する。もし多数決が1つのIPアドレス1票に基づく場合、沢山のIPを持つ誰かによって堕落されてしまう。 POWは基本的には1CPU1票である。多数決は最長のチェーンによって決まる。そのためにはPOWの努力への投資は最大になる。もしCPU能力の多数が正直なノードによって支配されるならば、正直なチェーンは最速で成長し、他の競合するチェーンを凌駕する。 過去のブロックを修正するには、攻撃者は当該ブロックとその後の全てのブロックのPOWをやり直しせねばならず、正直なノードの作業に追いつき凌駕しなければならない。後述するようにその後のブロックが引き続き追加されることで遅い攻撃者が追いつく確率は冪乗的に減少していく。 時間経過に伴いハードウェアの処理速度と操作するノードに対する様々な要求が増加することに対応して、POWの難しさは目標とする時間当たりの平均ブロック数となるように移動平均によって決められる。もし処理が早すぎる場合には難しさは増加する。

>Top 5. Network: The steps to run the network are as follows: New transactions are broadcast to all nodes. Each node collects new transactions into a block. Each node works on finding a difficult proof-of-work for its block. When a node finds a proof-of-work, it broadcasts the block to all nodes. Nodes accept the block only if all transactions in it are valid and not already spent. Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash. Nodes always consider the longest chain to be the correct one and will keep working on extending it. If two nodes broadcast different versions of the next block simultaneously, some nodes may receive one or the other first. In that case, they work on the first one they received, but save the other branch in case it becomes longer. The tie will be broken when the next proof-of-work is found and one branch becomes longer; the nodes that were working on the other branch will then switch to the longer one. New transaction broadcasts do not necessarily need to reach all nodes. As long as they reach many nodes, they will get into a block before long. Block broadcasts are also tolerant of dropped messages. If a node does not receive a block, it will request it when it receives the next block and realizes it missed one.

5. ネットワーク ネットワークの処理ステップは以下の通り。 新たな取引は全てのノードにブロードキャストされる 各ノードは新たな取引をブロックに収集する。 各ノードはそのブロックに対する難しいPOWを見つけて作業する。 あるノードがPOWを見つけると、それはそのブロックについて全てのノードにブロードキャストする。 複数のノードはその中の全ての取引が有効かつ消費されていない場合に限り当該ブロックを受領する。 複数のノードは、当該ブロックをチェーンの中に次のブロックとして作成することで受領したことを表示し、また受領した当該ブロックのハッシュをそれ以前のハッシュとして利用する。 複数のノードは常に最長のチェーンを正当なものとしてそれを延長するように作業を続ける。 もし２つのノードが次のブロックを同時に異なるバージョンでブロードキャストしてきた場合、あるノードは最初にそれを受領するかまたは他を受領することになる。 この場合、それらのノードは最初に受領したものを作業するか、それが長くなる場合に備えて別のブランチを保管する。次のPOWが見出されるとその連結は崩れて一つのブランチがより長くなる。他のブランチで作業していたノードは、より長い方のノードに切り替わる。 新たな取引のブロードキャストは必ずしも全てのノードに到達する必要はない。多くのノードに到達している限り、まもなくブロックを得ることになる。ブロックのブロードキャストは、メッセージの欠落に対しても寛容である。もしあるノードがあるブロックを受領しない場合、次のブロックを受領した時に再送の要求をして欠落したブロックを回復する。

>Top 6. Incentive: By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them. The steady addition of a constant of amount of new coins is analogous to gold miners expending resources to add gold to circulation. In our case, it is CPU time and electricity that is expended. The incentive can also be funded with transaction fees. If the output value of a transaction is less than its input value, the difference is a transaction fee that is added to the incentive value of the block containing the transaction. Once a predetermined number of coins have entered circulation, the incentive can transition entirely to transaction fees and be completely inflation free. The incentive may help encourage nodes to stay honest. If a greedy attacker is able to assemble more CPU power than all the honest nodes, he would have to choose between using it to defraud people by stealing back his payments, or using it to generate new coins. He ought to find it more profitable to play by the rules, such rules that favour him with more new coins than everyone else combined, than to undermine the system and the validity of his own wealth.

6. インセンティブ: 慣例として、ブロックの中の最初の取引はそのブロックの創造者によって所有されている新規コインとして開始する特別な取引である。これはそのネットワークを支援するノードに対するインセンティブとなり、コインを循環の中に最初に配布する方法となる。なぜならコインを発行する中央の権威が存在しないからである。我々の場合、消費されるのは、CPU時間および電気である。 一定量の新規コインが着実に追加されることは、金の採掘者がその資源を消費して、金を循環の中に追加することに例えられる。 そのインセンティブはまた取引費用によっても賄われる。もし取引による価値のアウトプットが、その価値のインプットよりも小さければ、その差額は取引費用となり当該取引を含むブロックのインセンティブ価値に加えられる。 一旦予め決められた数量のコインが循環されるようになるとインセンティブは取引費用となりインフレーションは発生しない。 このインセンティブはノードが正直であり続けることの支援となる。もし貪欲な攻撃者が全ての正直なノードよりもより多くのCPU能力を結集することができれば、彼は詐取した人々からその支払を盗み返すか、または、新たなコインの生成に利用できる。彼はルールによってもっと利益になることを見出そうとするはずであり、このようなルールとしては、システムに損害を与えるか、彼の富の有効期限を設けるよりも、彼に他の全ての人たちの合計よりも多くの新規コインを得るようになる。

>Top 7. Reclaiming Disk Space: Once the latest transaction in a coin is buried under enough blocks, the spent transactions before it can be discarded to save disk space. To facilitate this without breaking the block's hash, transactions are hashed in a Merkle Tree [7][2][5], with only the root included in the block's hash. Old blocks can then be compacted by stubbing off branches of the tree. The interior hashes do not need to be stored. A block header with no transactions would be about 80 bytes. If we suppose blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 = 4.2MB per year. With computer systems typically selling with 2GB of RAM as of 2008, and Moore's Law predicting current growth of 1.2GB per year, storage should not be a problem even if the block headers must be kept in memory.

7. ディスク空間の再利用: 一度、最新のコイン取引が十分なブロックの下に埋もれてしまえば、それより前に使用された取引はディスク空間を保つために棄却される。ブロックのハッシュ化を壊さないようにこの操作を行うには、取引はマークル木*としてハッシュ化され、ルートだけでブロックのハッシュに含まれる。古いブロックは木の枝を引き抜いて圧縮される。内部のハッシュは保存される必要はない。 取引のないブロックヘッダーは約80バイト。このブロックが10分毎に生成されるとすると、80 bytes×6×24×365=4.2 MB/年 (2008年)である。典型的なコンピュータは2GBのRAMで販売されている。ムーアの法則によれば、保存容量の伸び率は1.2GB/年ほどなので、ブロックヘッダーがメモリーに保存されたとしても問題にはならない。

<Fig.7> Reclaiming Disk Space:

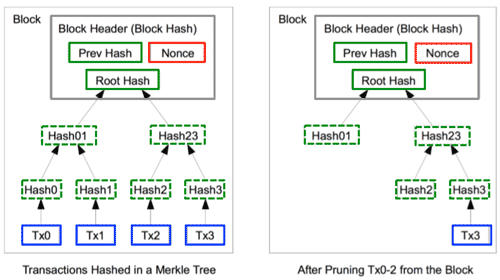
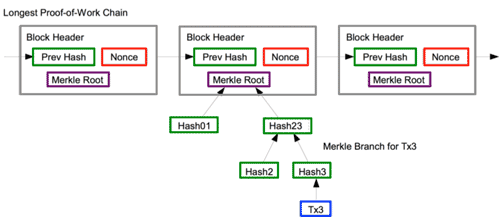
>Top 8. Simplified Payment Verification: It is possible to verify payments without running a full network node. A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he's convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it's timestamped in. He can't check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it, and blocks added after it further confirm the network has accepted it. >Top As such, the verification is reliable as long as honest nodes control the network, but is more vulnerable if the network is overpowered by an attacker. While network nodes can verify transactions for themselves, the simplified method can be fooled by an attacker's fabricated transactions for as long as the attacker can continue to overpower the network. (51% attack) One strategy to protect against this would be to accept alerts from network nodes when they detect an invalid block, prompting the user's software to download the full block and alerted transactions to confirm the inconsistency. Businesses that receive frequent payments will probably still want to run their own nodes for more independent security and quicker verification.	8. 簡便な支払認証: 全てのネットワークノードを通過しないで支払認証することは可能である。ユーザは最長のPOWチェーンのブロックヘッダーのコピーを保存するだけで、ネットワークノードへ問い合わせることで自身が最長のチェーンを有していることを確信でき、その取引が時刻認証しているブロックにリンクしているマークル木の枝を得る。自分では取引の検証はできないがチェーンの中の場所にリンクすることで、ネットワークノードがそれを受領したことを確認でき、ブロックがその後に追加されてネットワークがそれを受諾したことを確認できる。 このように、認証は正直なノードがネットワークを管理している限り信頼できるが、もしネットワークが攻撃者によって凌駕されると脆弱になる。ネットワークノードは自身で取引を認証できている間は、この簡便な方法では、攻撃者がネットワークを凌駕し続ける限り、攻撃者の偽造した取引によって騙される可能性がある。(51%攻撃) これを防ぐ一つの戦略は、ネットワークノードが無効なブロックを検知すると発する警告を受領することである。これはユーザのソフトウェアに対し全てのブロックをダウンロードして取引が無矛盾であることを確認するよう警告するのである。頻繁な支払を受け取るようなビジネスはおそらく自身のノードを更なる独自のセキュリティや迅速な認証のために操作する必要がでてくる。
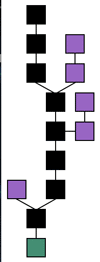
<Fig. 8> Simplified Payment Verification:	<Fig. 9> Combining and Splitting Value:	Block chain: Best & longest chain (black), while isolated chain (purple)

>Top 9. Combining and Splitting Value: Although it would be possible to handle coins individually, it would be unwieldy to make a separate transaction for every cent in a transfer. To allow value to be split and combined, transactions contain multiple inputs and outputs. Normally there will be either a single input from a larger previous transaction or multiple inputs combining smaller amounts, and at most two outputs: one for the payment, and one returning the change, if any, back to the sender. It should be noted that fan-out, where a transaction depends on several transactions, and those transactions depend on many more, is not a problem here. There is never the need to extract a complete standalone copy of a transaction's history.

9. 価値の合算と分割: コインを個別に扱うことは可能であろうが、移転に当たって各セントの単位まで個々の取引を行うのは非効率的である。価値を分割したり合算すれば、取引が複数のインプットとアウトプットを含む。通常、大きなそれ以前の取引からの単一のインプット、あるいは少額を合算しての複数のインプット、また１つの支払と１つの釣り銭を送り手に戻す場合のようにせいぜい2つのアウトプットまでである。 １つの取引が幾つかの取引に依存している場合やそれ以上の場合は、論理出力数(fan-out)と呼ばれるがはここでは特に問題とはならない。取引履歴から完全なスタンドアロンの取引を抽出する必要性は全くないからである。

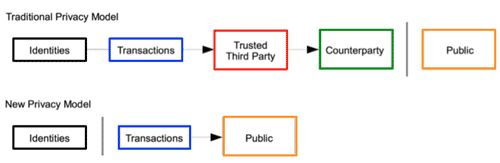
>Top 10. Privacy: The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party. The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous. The public can see that someone is sending an amount to someone else, but without information linking the transaction to anyone. This is similar to the level of information released by stock exchanges, where the time and size of individual trades, the "tape", is made public, but without telling who the parties were. As an additional firewall, a new key pair should be used for each transaction to keep them from being linked to a common owner. Some linking is still unavoidable with multi-input transactions, which necessarily reveal that their inputs were owned by the same owner. The risk is that if the owner of a key is revealed, linking could reveal other transactions that belonged to the same owner.

10. プライバシイ: 伝統的なバンキングモデルは、取引当事者および信頼できる第三者への情報を制限することで、一定のプライバシィを実現してきた。全ての取引を公開することはこの方法に反するが、プライバシィは別の場所で情報の流れを分断することで達成できる。即ち公開鍵は匿名だからである。公衆は誰かが誰かに送金したことはわかるが、取引を誰かに特定するよう情報がない。これは証券取引所によって公開される情報のレベルと同等である。そこでは個々の取引の時間とサイズの記録が公開されるが、その当事者は誰であるのかは非公開である。 もう一つのファイアウォールとしては、個々の取引でその都度使用される新たな1対の鍵は共通の所有者へつながってはいない。多数入力の取引では、一部のつながりは不可避となる。それによって多数入力が同一所有者のものであることが必然的に露出してしまう。もしあるキーの所有者が露見してしまうと、他の取引も同一所有者に属することが露見してしまうというリスクがあるという意味である。

<Fig.10> Privacy:

>Top 11. Calculations: We consider the scenario of an attacker trying to generate an alternate chain faster than the honest chain. Even if this is accomplished, it does not throw the system open to arbitrary changes, such as creating value out of thin air or taking money that never belonged to the attacker. Nodes are not going to accept an invalid transaction as payment, and honest nodes will never accept a block containing them. An attacker can only try to change one of his own transactions to take back money he recently spent. The race between the honest chain and an attacker chain can be characterized as a Binomial Random Walk. The success event is the honest chain being extended by one block, increasing its lead by +1, and the failure event is the attacker's chain being extended by one block, reducing the gap by -1. The probability of an attacker catching up from a given deficit is analogous to a Gambler's Ruin problem. Suppose a gambler with unlimited credit starts at a deficit and plays potentially an infinite number of trials to try to reach breakeven. We can calculate the probability he ever reaches breakeven, or that an attacker ever catches up with the honest chain, as follows [8]: $p$ = probability an honest node finds the next block $q$ = probability the attacker finds the next block $q_z$ = probability the attacker will ever catch up from z blocks behind $q_z=\begin{cases} 1 & if p\leq q \\ (\frac{q}{p})^2 & if p\gt q\\ \end{cases}$ Given our assumption that $p > q$, the probability drops exponentially as the number of blocks the attacker has to catch up with increases. With the odds against him, if he doesn't make a lucky lunge forward early on, his chances become vanishingly small as he falls further behind. We now consider how long the recipient of a new transaction needs to wait before being sufficiently certain the sender can't change the transaction. We assume the sender is an attacker who wants to make the recipient believe he paid him for a while, then switch it to pay back to himself after some time has passed. The receiver will be alerted when that happens, but the sender hopes it will be too late. >Top The receiver generates a new key pair and gives the public key to the sender shortly before signing. This prevents the sender from preparing a chain of blocks ahead of time by working on it continuously until he is lucky enough to get far enough ahead, then executing the transaction at that moment. Once the transaction is sent, the dishonest sender starts working in secret on a parallel chain containing an alternate version of his transaction. The recipient waits until the transaction has been added to a block and z blocks have been linked after it. He doesn't know the exact amount of progress the attacker has made, but assuming the honest blocks took the average expected time per block, the attacker's potential progress will be a Poisson distribution with expected value: $\lambda=z\frac{q}{p}$ To get the probability the attacker could still catch up now, we multiply the Poisson density for each amount of progress he could have made by the probability he could catch up from that point: $\displaystyle\sum_{k=0}^{\infty}\frac{\lambda^k e^{-\lambda}}{k!}\begin{cases}(\frac{q}{p})^{(z-k)} & if k\leq z\\ 1 & if k\gt z \end{cases}$ Rearranging to avoid summing the infinite tail of the distribution... $1-\displaystyle\sum_{k=0}^z\frac{\lambda^k e^{-\lambda}}{k!}\left(1-\left(\frac{q}{p}\right)^{(z-k)}\right)$ Converting to C code... #include <math.h> double AttackerSuccessProbability(double q, int z) { double p = 1.0 - q; double lambda = z * (q / p); double sum = 1.0; int i, k; for (k = 0; k <= z; k++) { double poisson = exp(-lambda); for (i = 1; i <= k; i++) poisson *= lambda / i; sum -= poisson * (1 - pow(q / p, z - k)); } return sum; } Running some results, we can see the probability drop off exponentially with z. q=0.1 z=0 P=1.0000000 z=1 P=0.2045873 z=2 P=0.0509779 z=3 P=0.0131722 z=4 P=0.0034552 z=5 P=0.0009137 z=6 P=0.0002428 z=7 P=0.0000647 z=8 P=0.0000173 z=9 P=0.0000046 z=10 P=0.0000012 q=0.3 z=0 P=1.0000000 z=5 P=0.1773523 z=10 P=0.0416605 z=15 P=0.0101008 z=20 P=0.0024804 z=25 P=0.0006132 z=30 P=0.0001522 z=35 P=0.0000379 z=40 P=0.0000095 z=45 P=0.0000024 z=50 P=0.0000006 Solving for P less than 0.1%... P < 0.001 q=0.10 z=5 q=0.15 z=8 q=0.20 z=11 q=0.25 z=15 q=0.30 z=24 q=0.35 z=41 q=0.40 z=89 q=0.45 z=340

11. 計算: 攻撃者の目論とは、正直なチェーンより別のチェーンをより早く発生させようとすることである。もしこれが実現されたとしてもシステムが勝手に変更されたりして、無から価値を創造したり、攻撃者のものでない金を詐取したりすることにならない。ノードは不正な取引の支払を認めないし、正直なノードはそれらを含めブロックを承認したりはしない。攻撃者は自分の取引の一部を変更して、攻撃者が直近で支出した金を取り戻すことができるだけのことである。 正直なチェーンと攻撃者のチェーンの間の競争は二項ランダムウォークとして知られる。正直なチェーンが１ブロック延長すれば成功で、そのリードは+1となる。失敗の場合は攻撃者のチェーンが１ブロック延長され、その差は-1となる。 攻撃者が与えられた不足から追いつく確率は、賭博師の破滅問題に似ている。無制限の与信をもつ賭博師が赤字から始まり無限回の試行を行い損益分岐点に到達すると想定する。我々は損益分岐点に到達する確率を計算でき、攻撃者は以下のように正直なチェーンに追いつく。 $p$ = 正直ノードが次のブロックを見つける確率 $q$ = 攻撃者ノードが次のブロックを見つける確率 $q_z$ = 攻撃者が zブロック後ろから追いつく確率 $q_z=\begin{cases} 1 & if p\leq q \\ (\frac{q}{p})^2 & if p\gt q\\ \end{cases}$ $p > q$の前提とすると、攻撃者が追いつかなければならないブロック数が増加するに伴い、その確率は冪乗的に減少する。攻撃者に対する可能性は、初期段階でラッキーな飛び出しををしなければ、彼のチャンスは後になるほどゼロになるように小さくなる。 新たな取引の受取人は、 送金者がその取引を変更できないよう十分確実になるまでにどの位時間がかかるのだろうか。送金者が攻撃者であり、受取人が送金者の送金をしばらく信じさせるように仕組み、その後一定時間後に自分自身の送金を戻すようにするものと想定してみる。受取人はそのことが発生した時に警告を受け取ることになるが、送金者としてはそれが遅すぎることを願っている 受取人は新たな鍵のセットを生成し、署名後直ぐに公開鍵を送金者に送る。このことが送金者が連続して作業することでブロックチェンの予定より早く準備することを防ぎ、その後でその取引をその時点で実行する。取引が一旦送られてしまえば、不実な送金者は自分の取引機の変更版を含む平行するチェーンを密かに作業開始することになる。　　　　　　　 受取人は当該取引がブロックに追加され、zブロックがその後にリンクされているのを待つことになる。受取人は攻撃者が行った正確な進展の数量を知らないが、誠実がブロックがブロック当たりの平均的な時間を想定することで、攻撃者の進展の可能性は、期待値に対するポアソン分布となる。 $\lambda=z\frac{q}{p}$ 攻撃者がまだ追いついていない確率は、ポアソン濃度に各進展の数量を掛ければ､攻撃者が追いつくである確率を計算できる。 $\displaystyle\sum_{k=0}^{\infty}\frac{\lambda^k e^{-\lambda}}{k!}\begin{cases}(\frac{q}{p})^{(z-k)} & if k\leq z\\ 1 & if k\gt z \end{cases}$ 分布の無限のテールを合計するのを避けて再編すれば、 $1-\displaystyle\sum_{k=0}^z\frac{\lambda^k e^{-\lambda}}{k!}\left(1-\left(\frac{q}{p}\right)^{(z-k)}\right)$ これをCコードに変換すれば、 #include <math.h> double AttackerSuccessProbability(double q, int z) { double p = 1.0 - q; double lambda = z * (q / p); double sum = 1.0; int i, k; for (k = 0; k <= z; k++) { double poisson = exp(-lambda); for (i = 1; i <= k; i++) poisson *= lambda / i; sum -= poisson * (1 - pow(q / p, z - k)); } return sum; } 一部結果を示すと、その確率はzと共に冪乗的に減少する。 q=0.1 z=0 P=1.0000000 z=1 P=0.2045873 z=2 P=0.0509779 z=3 P=0.0131722 z=4 P=0.0034552 z=5 P=0.0009137 z=6 P=0.0002428 z=7 P=0.0000647 z=8 P=0.0000173 z=9 P=0.0000046 z=10 P=0.0000012 q=0.3 z=0 P=1.0000000 z=5 P=0.1773523 z=10 P=0.0416605 z=15 P=0.0101008 z=20 P=0.0024804 z=25 P=0.0006132 z=30 P=0.0001522 z=35 P=0.0000379 z=40 P=0.0000095 z=45 P=0.0000024 z=50 P=0.0000006 Solving for P less than 0.1%... P < 0.001 q=0.10 z=5 q=0.15 z=8 q=0.20 z=11 q=0.25 z=15 q=0.30 z=24 q=0.35 z=41 q=0.40 z=89 q=0.45 z=340

注: Gamler's ruin: a gamler who raises his bet to a fixed fraction of bankroll when he wins, bus does not reduce it when he loses, will eventually go broke, even if he has a positive expected value on each bet.

>Top 12. Conclusion: We have proposed a system for electronic transactions without relying on trust. We started with the usual framework of coins made from digital signatures, which provides strong control of ownership, but is incomplete without a way to prevent double-spending. To solve this, we proposed a peer-to-peer network using proof-of-work to record a public history of transactions that quickly becomes computationally impractical for an attacker to change if honest nodes control a majority of CPU power. The network is robust in its unstructured simplicity. Nodes work all at once with little coordination. They do not need to be identified, since messages are not routed to any particular place and only need to be delivered on a best effort basis. Nodes can leave and rejoin the network at will, accepting the proof-of-work chain as proof of what happened while they were gone. They vote with their CPU power, expressing their acceptance of valid blocks by working on extending them and rejecting invalid blocks by refusing to work on them. Any needed rules and incentives can be enforced with this consensus mechanism.

12. 結論: 我々は信用に基づかない電子取引のシステムを提案してきた。それはデジタル署名による通常のコインのフレームワークから始めた。この枠組みは、所有権を強力にコントロールするが、二重支払を防止する方法がないという点では不完全である。 これを解決するために、我々はPOWを利用して取引の公開履歴を記録するP2Pのネットワークを提案した。これにより誠実なノードが多数のCPU能力を管理している限り、攻撃者は計算上変更を加えることが不可能となる。。 このネットワークは組織化されていない簡潔さにおいて堅牢である。ノードはほとんど協調なしに同時に行われる。それらは特定される必要もないし、メッセージが特定の場所に向かうこともなく、ベストエフォットベースで伝達されるだけである。 ノードはネットワークを自由に分離し、また加入し、不在時の出来事の証明としてPOWチェーン認証する。ノードはそれらのCPU能力として投票し、ブロックを延長する作業をすることで有効なブロックの受諾を表示し、また不正なブロックを拒否することで不正を排除する。全ての規則とインセンティブはこれを合意するメカニズムによって強化される。

PS-1

>Top 13. PS-1: Problems of the Blockchain, etc: Scalability: The current Blockchain limits its size not more than 1MB, which averagely takes 10 minutes to settle the Blockchain. (The average performance is said theoretically 7 Blockchains per second, while the conventional transactions are around 2000 per second.) Segregated Witness (SegWit): This function is originally included in the Bitcoin software to extend transaction ability (called Transaction Malleability). But the SegWit is off at the moment, whose change is required to get not less than 95% support from the miners. Difficulty to get the consensus of the system changes is regarded as a fate of P2P network. >Top The upper limit of Blockchain: More drastic idea to abolish 1MB limit of the block size is proposed by a group called 'Bitcoin Unlimited', which is supported by some miners. But this change means to make another branch of Blockchain which is incompatible with the present system. (Hard Fork) Time needed to settle the transaction: About 10 minutes required for settlement of the blockchain is slow and inconvenient considering more frequent and smaller transactions. >Top Energy waste for POW: Calculating of Hash values consumes enormous computer powers (electricity charges), which is valueless activity and waste of resources. (called Hash Power) Actually the majority of mining activity is done is remote areas in China, where the electric power is cheaper. Consensus Algorithm: POW (Proof of Work): influence determined by high Hash power (=electric power) POS (Proof of State): influence determined by stake (=volume of ownership of coins) POI (Proof of Importance): influence determined by importance of the business; i.e., volume of ownership of coins and transactions. POH (Proof of Human-work): influence determined by the answer of human work, not of the computer. Expansion of data: Blockchain of Bitcoin published all data of transactions, which is destined to increase. Weakness of anonymity: The flow of transactions could be lineally tranced if the owner is identified; thus new address is usually used at each transaction to keep anonymity, which has not necessarily strong anonymity. However, strong anonymity could be misused as money laundering. >Top Authenticity of Blockchain: Blockchain is extremely difficult to be falsified; but not be be guaranteed its authenticity of the content. The message embedded in the Blockchain remain the fact of making the message on a particular date and time, but the content of the message could not be guaranteed whether it is true or not. >Top Multi-signiture (M of N): Transaction is defined to require multi-signiture, requiring M numer of public keys out of N number of registered public keys. This mechanism can be used in triple partners transaction, such as Esclow transaction; among incredible partners of seller, buyer, and the third party. >Top UTXO (Unspent Transaction Output): One transaction consists of multiple remmitances (output) including remittance the balance to oneself. In the Blockchain, the output of unspent balance is called UTXO. New transactions are created from this UTXO; which is separately stored on the memory to be quickly processed in the Blockchain. >Top Function of Wallet: In the Blockchain, wallet has the following function. Making and saving Secret Key; including managing correspoinding Public Key and Address. Making of transaction, signiture, and its remittance. Managing of information relating to the address. Such wallet is not necessarily required to be online; Cold Wallet (offline) and Hot Wallet (online) The range of verification of Blockchain by wallet: Full Node: requires 100GB data to verify all Blockchain. SPV (Simplified Payment Verification): verfying own transaction only. Service use only: consists of minimum information, without verificaltion; relying on API of the server.

追記1: ブロックチェーンの課題等: スケーラビリティ: 現状のブロックチェーンは1MB以下で、その取引完了までには平均10分かかる。(理論的には毎秒7ブロックチェーンの効率。従来の取引効率は毎秒約2000件。) Segregated Witness (SegWi): ビットコインのソフトウェアに当初から組み込まれた機能で。互換性を保ったまま取引の処理数の増加が可能 (トランザクション展性) 但し、現在この機能はOffで、その変更にはマイナーの95%以上の賛成が必要。 システム変更の合意を得るのが難しいのはP2Pネットワークの宿命とも言える。 Blockchainの上限: ブロックサイズの上限1MBを撤廃する提案がBitcoin Unlimitedというグループから提案され、一部のマイナーから支持されている。 但し、この変更は現在のソフトウェアとの非互換的なブロックチェーンの分岐を作ることを意味する。(ハードフォーク) 取引確定までの時間: 取引確定までのかかる約10分間は、頻繁かつ少額取引を考慮すると遅いし不便である。 POWのエネルギー浪費: ハッシュ値の計算には、膨大なコンピュータパワー(電気料金)がかかり、これは価値のない活動かつ資源の無駄遣いである。(ハッシュパワーと呼ばれる) 実際には、大半のマイニング作業は、中国の僻地の電気料金の安い地域で行われている。 コンセンサス･アルゴリズム: POW: 高ハッシュ･パワーによる影響力 POS: コイン所有量による影響力 POI: コイン所有量と取引量による影響力 POH: コンピュータでなく、人間による回答による影響力 データの肥大化: ビットコインのブロックチェーンは取引履歴の全データを公開しているので、時間と共に増大する。 匿名性の弱点: 一旦所有者が特定されると、取引の流れが直線的に判明してしまう。このため匿名性を保つために、取引毎に新たなアドレスが使われる。 但し、強い匿名性はマネーロンダリングに悪用される可能性がある。 ブロックチェーンの真正性: ブロックチェーンは改竄されにくいだけで、そのデータの真正性は保証されない。 ブロックチェーンにメッセージを埋め込むことで、その日時に発言を行った事実は残るが、その他の真正性は保証されない。 マルチシグネチャ (M of N): 登録されたN個の公開鍵の内、N個を要求することで取引を有効にする方法。 この機能は、エスクロー取引のような三者間取引に使用可能である。即ち信用できない売手、買手、第三者間の取引である。 UTXO: 一つの取引は、自分自身への残高送金を含め複数の送金からなっている。 ブロックチェーンでは、未使用残高はUTXOと呼ばれる。 新たな取引はこのUTXOから生成されるので、ビットコインのシステムでは、別のメモリ上に常駐させ、迅速処理できるようにしている。 Walletの機能: ブロックチェーンでは、Walletは以下の機能を有する。 秘密鍵の作成と保有: 対応する公開鍵･アドレスの管理 取引･署名の作成とその送信 アドレスに関する取引情報の管理 Walletは、オンラインである必要はない。Cold Wallet (offline) とHot Wallet (online)がある。 ブロックチェーンの検証範囲: Full Node: 全てのブロックチェーンを検証するた100GBのデータが必要 SPV: 自身の取引のみ検証する方法 サービス利用型: APIを提供するサーバを信用して検証は行わず必要な情報のみ取得する方法

PS2

>Top 14. PS-2: Expansion of the Blockchain: Bitcoin 2.0: This is alternative non-virtual coin applications of the blockchain technology which is used for Bitcoin. Smart Contract: a mechanism that a certain condition is embedded in the blockchain of Bitcoin, and if the condition is satisfied, the program is automatically executed. >Top Ethereum is a kind of such Smart Contract. Ethereum is published on 2/Jan./2014. Public but non-permitted transactions. uses unique Blockchain; there are miners who earn the other coin named Ether. The time required settlement of Blockchain is about 15 seconds. Programming language Solidity is prepared to develop Ethereum Blockchain Ethereum keeps balance status of the account (unlike Bitcoin). Two accounts are defined: EOA (Externally Owned Account) used by a public user, and Contact Account to record the deployed smart contracts. Such smart contracts can execute various programs stored in other real Web servers such as stock price, weather forecast, etc. Miners' commission is called Gas, which is a kind of virtual fuel to pay for the maintenance of Ethereum system. Hyperledger Project: this is a project of The Linux Foundation, supported by major companies such as IBM, Intel, Fujitsu, Hitachi, Accenture, J.P. Morgan, etc. >Top Hyperledger Fabric: typical project developed by IBM. (on BlueMix of IBM cloud platform) published on 17/Sept./2016 Private (non-public) and permitted transactions. use unique Blockchain Conventional computer languages (Go, Java, etc.) are used; various module software is published; including: 1) Membership service: managing identity, privacy, confintiality, and auditability of the member; like the funciton of CA (Certificate Authority). 2) Blockchain service: managing distriuted ledger trough p2p protocol built on HTTP/2.; available plug-in to different consensus (PBFT, Raft, PoW, PoS) 3) Chaincode service: providing a secured and lightweight way to sandbox the chaincode execution on the validating nodes. aims to replace existing systems by Fabric Blockchain technology. (but still experimental stage) >Top PBFT (Practical Byzantine Fault Tolerance)*: This is a consensus algorithm, operated by the centralized system (unlike Bitcoin). Two peers: 1) Validating peers who choose the leader , and 2) Non-validation peers. All transactions are transferred to validating peers; the leader verifies non-falcification of the transaction data. (quicker POW in seconds) The status by the latest transaction is recorded in the World State database. (Key Value Store) Fabric is a smart solution to perform transactions among consortium composed of financial or logistic companies. >Top Ripple service: developed by Canadian Ryan Fugger in 2004, aiming not to produce virtual currency. Ripple prepares its native coin named XRP; but aiming to exchange among other currencies such as US$, Japanese ¥, Gold, Bitcoin, etc. (like a borderless banking network) Public but permitted transactions. Ripple keeps the status account called Ledger, instead of Block. Supported by J.P. Morgan, Credit Suisse, Bank of America, Mitsubishi-UFJ, Mizuho, Risona Bank, etc. Gateway of Ripple network issues IOU, a kind of debit note, finally exchanging with real currencies. IOU looks like LC (Letter of Credit) or bank note. Transactions are approved by a certain centralized Validater authorized in UNL (Unique Node List); the transaction is finalized by not less than 80% approvals by the Validaters. Validaters function to avoid fork situation of Blockchain and expensive POW and no commissions for miners as well as enabling rapid settlement. But Ripple prepares some commission to prevent spam attacks as a defensive measures. (number of signs times 10 drops (=0.0001 XARP)) XRP is defined to confine its data size (caused by cyber attack), keeping minimum data volumes named Reserves as the latest status, whose latest status is easily stored in user's PC. Conventional international financial transactions have needed expensive commission and several days for settlement due to different infrastructure of each nation. This Ripple system could minimize interbank transactions. But frequent fluctuations of XRP by speculation could be a risk factor as the bridge currency.

ブロックチェーンの広がり: ビットコイン2.0 ビットコインの技術を利用して、通貨ではない他の機能に応用すること。 スマートコントラクト: ビットコイン上で実行されるプログラムに、ある条件が埋め込まれ、条件が満たされた時に、そのプログラムが自動的に実行される仕組み。 Ethereumは独自のブロックチェーンを利用するスマートコントラクトの一つ。 Ethereumは2014/1/2に公開。 プライベート(非パブリック)ブロックチェーン: ユニークなブロックチェーン。コイン名はEther. ブロック生成時間は、約15秒。 Etherコインを得るマイナーが存在。 プログラミング言語 Solidityを準備。 Ethereumはアカウント残高を保持 ２つのアカウント: EOAとContractアカウント 株価、天気予報等Webサーバを実行するスマート契約が可能 マイナー手数料はGas。システム保持に使用。 Hyperledgerプロジェクト: The Linux Foundationのプロジェクトで、IBM, Intel, 富士通, 日立, Accenture, J.P. Morgan等が支援。 Hyperledger Fabric: IBMが開発した。IBMのクラウド・プラットフォーム BlueMixで提供。 2016/9/17に公開 ユニークなブロックチェーンを利用 従来のコンピュータ言語(Go, Java等)を活用。様々なモジュールが公開。以下モジュールから成る。 メンバーシップサービス: 参加者の認証･管理 (CA局の機能) ブロックチェーンサービス: 異なるプラグインを通じてブロックチェーンを管理 チェーンコードサービス: 取引の実行･保存 既存システムをFabric Blockchain技術での置き換えを狙う。まだ実証実験段階。 PBFT (Practical Byzantine Fault Tolerance): これはHyperledgerで利用される中央集権型のコンセンサス・アルゴリズム (Bitcoinとは異なる)。 リーダーを介してトランザクション処理が行われる。POWが迅速化される。 最終の取引によるステータスは、World Stateデータベースに記録される。(Key Value Store) Fabricは、金融･物流などの組織からなるコンソーシアム内取引のプラットフォームとしては優れたソリューション。 Rippleサービス: カナダのRyan Fuggerによって2004年に開発。仮想通貨を目的としていない。 Rippleは、ネイティブ通貨XRPを準備しているが、その目的は、米ドル･円･金･ビットコイン等間の為替取引。(ボーダレスの銀行ネットワーク) パブリックで、許可型のトランズアクション。 Rippleは、Blockの代わりに、Ledgerと呼ばれる残高台帳を保存する。 J.P. Morgan, Credit Suisse, Bank of America, 三菱UFJ, みずほ, りそな銀行などが利用検討中。 Rippleネットワークのゲートウェイは 借用書であるIOUを発行･取引する。 IOU は信用状または銀行手形に似ている。 取引は、UNLと呼ばれる承認リストに規定された中央集権的なValidatorが, 全Validatorの80%以上の賛成によって取引承認が行う。 Blockchainのようなフォークによる台帳分岐のリスクがない マイニングのためのPOWの大量計算が不要で、多額の手数料も不要で、高速決済が可能 但し、Ripple はスパム防止策としての最低手数料を設定している。（著名数☓10 drops） XRPは Ledgerのデータ量が増加しないようにResrevesと呼ばれる最低保有量を設定している。PC等に取引の最終状態を保存される。 従来の国際金融取引には、各国の銀行間取引のインフラの違いにより、多額の手数料と取引に吸うを必要としてきた。このRippleシステムは銀行間取引を最小化する可能性がある。 但し、XRPが投機によって頻繁に変動するのはブリッジ通貨としてはリスクとなる。

>Top * Byzantine Generals Problems: "The Byzantine Generals Problem: a group of general encircle Constantinople. These general wish to formula a plan for attacking the city: the generals must decide only whether to attack or retreat. The important thins is that every general agree on a common decision. The problem is complicated by the presence of treacherous generals who may not only cast a vote for a suboptimal strategy, they may do so selectively. For instance, if nine generals are voting, four support attacking while four others are in favor of retreat the ninth general may send a vote of retreat to those generals in favor of retreat, and a vote of attack to the rests. The problem is complicated further by the generals being physically separate and having to send their votes via messengers who may fail to deliver votes or may forge false votes. Byzantine fault tolerance can be achieved if the loyal generals have a majority agreement on their strategy. There can be a default vote value given to missing message <Null>. Further, if the agreement is that the <Null> votes are in the majority, a pre-assigned default strategy can be used (e.g., retreat). Suppose we have a traitorous Commander A, and two Lieutenants, B and C: when A tells B to attack and C to retreat, and B and C send messages to each other, forwarding A's message, neither B nor C can figure out who is the traitor, since it is not necessarily A - another Lieutenant could have forged the message purportedly from A. It can be shown that if n is the number of generals in total, and t is the number of traitors in that n, then there are solutions to the problem only when n > 3t and the communication is synchronous (bounded delay).

ビザンチン将軍問題: オスマン帝国の将軍達が、各々の軍団を率いてコンタンティノープルを包囲している状況とする。将軍達は都市攻撃計画について合意したいと考えている。将軍対の決定は、攻撃するか撤退するかである。問題を複雑にしているのは、一部の将軍達が反逆者であって、時折、最適でない戦略に投票したりして混乱させることである。 例えば、9人の将軍が投票するとして、その内4人が攻撃に投票し、他の4人が撤退に投票した場合、9人目の(反逆者でもある)将軍は、撤退案の将軍達には徹底票を送り、攻撃案の将軍達には攻撃票を送ることができる。 更に問題を複雑にするのは、将軍達が物理的に離れた場所にいるため、使者のへ託した投票信書を届けるのに失敗する場合もあるし、偽の票に改竄される可能性もあることである。 もし誠実な将軍達が戦略の過半数に合意すれば、この問題は解決する。 また未着の通信は<Null>として扱い、もし<Null>が多数となれば、予め決めた戦略(例: 撤退) が採用されるという方法もある。 裏切りの司令官Aとその副官B, Cがいるとする。AはBに攻撃を、Cには撤退を告げ、B/Cは各々の信書を伝達するが、BもCも誰が裏切り者かは特定できないし、他の副官はAの指示で改竄したかもしれない。 nを全将軍数とし、tをnの中の裏切り者の将軍数とすると、n>3tの場合だけは解決が可能となり、通信は時間制限内で同期的となる。

Com.

>Top Bitcoin system uses classic or proven encryption technology, and is a typical good sample to study robustness of the mechanism. Mechanism and usage of Bitcoin has made the Internet more open, secure network, bridging virtual and real worl; there is no physical coins, but credit and book-keeping connecting nodes have enabled it. Why Japanese government or banks, or the national are not challenging to develop this system, even though the creator's name, Satoshi Nakamoto is a typical Japanese name. All business is promoted between credibility and discredibility. POW relates to energy consumption or enegetic labors, POS to capitals or finance, POI to capital, finance, and business partners, and POH to human ability or creativeness.

ビットコインは古典的で実証済の暗号化技術を使っておりメカニズムの堅牢さを研究する良い事例である。 ビットコインのメカニズムと利用はインターネットをよりオープンから安全なネットワークにして、仮想と現実の世界に橋をかけた。物理的なコインは存在していないが、ノードをつなぐ信用と帳簿がそれを可能にした。 なぜ日本政府、日本の銀行、国民はこのシステムをもっと発展させようとしないのか。この創造者は典型的な日本の名前、"ナカモトサトシ (中本哲史?)"であるにも関わらずである。 全てのビジネスは信用と不信用の間で行われている。POWはエネルギー消費や活発な労働に関連し、POSは投融資に、POIは投融資+ビジネス取引に、そしてｓPOHは人間の能力や創造性に関連している。