>Note
Brief Calculus
Cat: SCI
Pub: 2015
#:1612b
Benjamin Crowell
16621u/18227r
Title
Brief Calculus
簡単な微積分
Index
Key
; drivative; fluxions; hyperreal number; infinitesimal; polynominal; standard part;
Résumé
Remarks
>Top 1. Rate of change:
- 1.1: Change in discrete steps:
- A German elementary school teacher asked the pupils to add up all numbers from 1 to 100:
- A boy named Carl Friedrich Gauss had a flash of insight of his answer; 5,050.
- The sum of n numbers will be (n2+n)2
- if ˙x is a polynomial of a certain order, then x must be a polynomial with an order greater by one.
- 1.2: >Top Continuous change:
- Issac Newton in 1660s: he was dealing with the continuous flow of change; called 'fluxions', known as the calculus.
- slope of the line drawn between neighboring points; referred to as the tangent line.
- Higher-order polynomials:
- Interpreting 1 as t0, we detect what seems to be general rule, which is the derivative of tk is ktk−1
- 1.3: >Top The second derivative: acceleration a
- ˙x=at, and x=at22
- ¨x=a
1. 変化率:
- an inflection point
- the edge of the function's domain
- a point where the function isn't differentiable.
- Fluxions, 流率法
>Top 2. To infinity - and beyond!:
- 2.1: Infinitesimals:
- Gottfried Leibniz (1648-1716):
- Calculus is really about numbers that are infinitely small: infinitesimals.
- mistake impression that infinitesimals exist in some remote fairyland where we can never touch them.
- Infinitesimals are not more or less mysterious than irrational numbers, and in particular we can represent them concretely on a computer.
- d represents an infinitesimally small number, such as dx and dt
- d is a positive number than is less than any positive real number.
- >Top Abraham Robinson (1918-1974):
- calls it is the hyperreal number system, which includes the real numbers as a subset.
- For a nonzero real number a, there is no real number b such that a=0b.
This means that we can't divide a by 0 and get b.
- Division by zero is undefined. However we can divide a finite number by an infinitesimal, and get an infinite result.
- Bishop George Berkeley (1685-1753):
- criticized infinitesimals; "they are neither finite quantities, nor quantities infinitely small,, nor yet nothing. May we not call them ghosts of departed quantities?"
- 2.2 Safe use of infinitesimals:
Hyperreal number system: introduced by Edwin Hewitt in 1948.
- includes the real numbers as a subset.
- Transfer principle: Suppose it's possible to translate it into a statement about the hyperreals in the most obvious way, simply by replacing the word real with the work hyperreal. The the translated statement is also true.
- doesn't apply to: "For any real number a, there is an integer n that is greater than a."
- Because: there is at least one hyperreal number, H, which is greater than all the integers.
- >Top dt:
- every number as being surrounded by a halo of numbers that don't equal it, but differ from it by only an infinitesimal amount.
- every integer is surrounded by a bunch of fractions that would round off to that integer. We can define the standard part (st) of a finite hyperreal number.
- the standard part of 2t+dt is 2t.
- dt2 is infinitesimally small compared to the infinitesimal dt; dt2 is a submicroscopic flea that lives on the flea. (doggerel); 1.0012=1.0002001
- dydx=limΔx→0ΔyΔx
- 2.3: The product rule:
- If x and y are both functions of t, then the derivative of their product is:
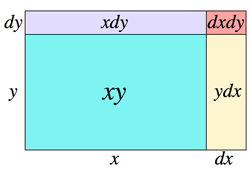
- d(xy)dt=dxdty+xdydt
- ∵(x+dx)(y+dy)−xy=ydx+xdy+dxdy, dividing by dt makes into:
dxdty+xdydt+dxdydt, whose standard part is the result bo be proved.
- d(tsint)dt=td(sint)dt+dtdtsint=tcost+sint
- Leibniz notation
- 2.4: The chain rule:
- dzdx=dzdy+dydx
- if a change in x causes y to change, and y then causes z to change; cascading effect.
- 2.5: Exponentials:
- dexdx=ex+dx−exdx=exedx−exdx=exedx−1dx=cex
- The second factor is a constant, c.
- dcdt=−c0ae−ta
- the rate at which caffeine is being removed from the blood and broken down by the liver; negative means the concentration is decreasing; large a will take a long time to reduce.
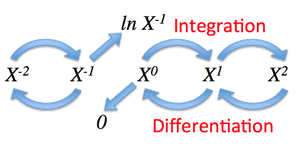
- The integral of x−1 is not x00. Likewise, the derivative of x0=1 is 0x−1=0. The function xn form a kind of ladder, with differentiation taking us down one rung, and integration taking us up. (>fig.)
- y=10x,lny=xln10,y=exln10⇒dydx=exln10ln10
- Logarithm:
- The natural logarithm is the function that undoes the exponential.
- y=lnx,x=ey⇒dxdy=ey,dydx=1ey=1x∴dlnxdx=1x
- Prove d(xn)dx=nxn−1 for any real value of n, not just an integer.
- y=xn=enlnx
- By the chain rule,
dydx=dnlnx・nx=xn・nx=nxn−1
- 2.6: Quotients:
- So far we've been successful with a divide-and-conquer approach to differentiation:
- New notation: it would be more common to write like this: dvudx→ddx(vu)
- Using the new notation, the quotient rule becomes:
ddx(vu)=1u・dvdu−vu2・dudx
- Definition of the limit:
- limx→af(x)=l
- for any real number ϵ, there exists another real number δ such that for all x in the interval a−δ≤x≤a+δ, the value of f lies within the range from l−ϵ to l+ϵ.
- In terms of infinitesimals; the limit of f(x) as x approached a, written:
limx→af(x)=l
for any infinitesimal number dx, the value of f(a+dx) is finite, and the standard part of f(a+dx)=l.
2. 無限、その先へ:
- 2.1: Infinitesimal, 無限小: a value approaching zero, but not zero.; 'infinite-th' item in sequence
- Tranfer principle:
The idea is to express analysis over R in a suitable language of mathematical logic, and then point out that this language applies equally well to *R.
- 2.2. 超実数
- 2.3: Product rule:
- 2.5: Exponetial function ex, where e=2.71828...
comes up in applicatis as diverse as credit card interest, groth of populations, and electric circuits.
- There are 2 special cases where differentiation takes us off the ladder entirely.:
>Top3. Limits and continuity:
- 3.1 Continuity:
- Continuous function; whose graph has no sudden jumps in it; can be drawn without picking the pen up off of the paper.
- f(x) is defined to be continuous if for any real x and any infinitesimal dx,f(x+dx)−f(x) is infinitesimal.; which is not differentiable at that point.
- (>Fig.) since dx>0,f(0+dx)−f(0)=1,which isn't infinitesimal.
- y=|x| shows that a function can be continuous without being differentiable.
- f(x)=h(g(x)); the composition of two continuous functions is also continuous.
- f(x)=1x is continuous everywhere except at x=0.
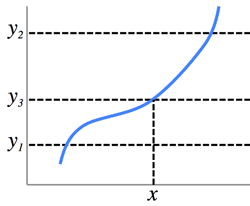
- The intermediate value theorem:
- (>Fig.): if the function is continuous, it must pass through y3
- <e.g.-11> dxdt=sin(t+dt)−sintdt=sintcosdt+costsindt−sintdt
small-angle approximations: sinu≈u and cosu≈1, we have:
dxdt=costdtdt+...=cost+...
- 3.2 Limits:
- Calculus of infinitesimals was created by Newton and Leibniz, and was reinterpreted in 19C by Cauchy, Bolzano, and Weierstrass in terms of limits.
- Every statement about limits was really a statement about infinitesimals.
- Weierstrass definition of the limit:
limx→af(x)=l; for any real number ϵ, there exits another real number δ such that for all x in the interval a−δ≤x≤a+δ, the value of f lies within the range from l−ϵ to l+ϵ.
- Another definition of the limit:
for any infinitesimal number dx, the value of f(a+dx) is finite, and the standard part of f(a+dx) equals l.
- This means that the derivative can be defined entirely in terms of the real number system, without the user of hyperreal numbers.
- 3.3 L'Hôpital's rule (simplest form):
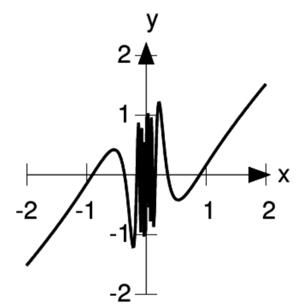
- (>Fig.) Consider the limit: limx→0sinxx
- Plugging in doesn't work, because we get 00.
- For small value of x, the small-angle approximation sinx≈x obtains.
- If u and v are function with u(a)=0,v(a)=0, the derivative ˙u(a) and ˙v(a),(≠0) are defined, then, limx→auv=˙u(a)˙v(a)
- e.g.: limx→0sinxx=cosx=1
- In terms of infinitesimals;
limx→0sinxx=st[sin(0+dx)0+dx]=st[dx+...dx], where we've used sin(p+q)=sinpcosq+sinqcosp, and ... stands for terms of order dx2.
So, limx→0sinxx=st[1+...dx]=1
- This limit is the same one we would use if we were evaluating the derivative of the sine function, applying the definition of the derivative as a limit.
- If u and v are function with u(a)=0 and v(a)=0, the derivative ˙u(a) and ˙v(a) are defined, and not zero, then: limx→auv=˙u(a)˙v(a).
- Proof: Since u(a)=0, and the derivative dudx is defined at a,u(a+dx)=du is infinitesimal, and likewise for v. By the definition of the limit, the limit is the standard part of uv=dudv=dudxdvdx
- 3.4 Another perspective on indeterminate forms:
- An expression like 00, called an indeterminate form
- 3-5: Limits at infinity
3. 極限値と連続:
- Continuity:
black dot indicated the endpoint is part of the ray, wile white one isn't.
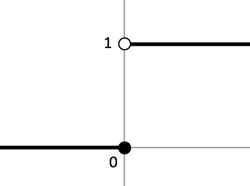
- f(x)=0;x≤0 and f(x)=1;x>0
- Intermediate value theorem:
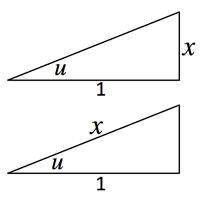
- let: x=g(t):
∫f(x)dx=∫f(g(t))g′(t)dt
let: g(x)=t
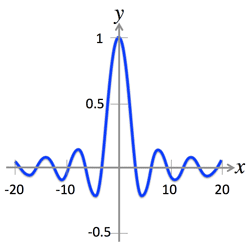
- The graph of sinxx:
>Top 4. Integration:
- 4.1: Definite and indefinite integrals:
- Integration and differentiation are inverse operations; integration undoes differentiation, or vice versa.
- Averages:
- ˉy=1b−a∫baydx
- The mean value theorem:
- If the continuous function y(x) has the average value ˉy on the interval from x=a to b, then y attains its average value at least once in that interval, i.e., there exists ξ with a<ξ<b such that y(ξ)=ˉy.
- Special case; ˉy=0 is known as Rolle's theorem.
- Work:
- When a force F acts on an object in the direction of the force by an infinitesimal distance dx, the infinitesimal work done is dW=Fdx; we have W=∫baFdx
4. 積分:
- 4.1: 定積分と不定積分:
>Top 5. Integration Techniques:
- 5.1: Newton's method:
- We now how to calculate the function y=x3 fairly accurately
- Δx=ΔxΔyΔy≈dxdyΔy=Δydydx=Δy3x2
- 5.2 Implicit differentiation:
- Eg.: y7+y=x7+x2
- d(x2)=d(x2)dxdx=2xdx; doing this to both sides of the original equation:
- 7y6+dy=y6xdx+2xdx
dydx=7x6+2x7y6+1
- 5.3 Methods of integration:
- Eg.: ∫dx2x+1=∫dx2x+1=∫du2u=12lnu+c=12ln(2x+1)+c;(u=2x+1)
- Integration by parts:
- ∫f(x)g′(x)=f(x)g(x)−∫f′(x)g(x)
or d(uv)=udv+vduudv=d(uv)−vdu
Integrating both sides:
∫udv=uv−∫vdu
- Partial fractions:
- Eg.: −1x−1+1x+1=−2x2−1 (we wouldn't have know how to integrate it.)
- the original form is easily integrated to give:
∫(−1x−1+1x+1)dx=−ln(x−1)+ln(x+1)+c
- Evaluate: ∫dx1+x2
- The substitution that works is x=tanu
tan2u+1=sec2u
dx=d[sinu(cosu)−1]=(dsinu)(cosu)−1+(sinu)d[(cosu)−1]=(1+tan2u)du=sec2udu
- So the integral becomes:
∫dx1+x2=∫sec2udusec2u=tan−1x+C
- ∫dx√1−x2
the substitution x=cosu
dx=−sinu,√1−x2=sinun
The result is:
∫dx√1−x2=∫−sinudusinu=−u+C=−cos−1x
- Eg: udv=(x)(cosxdx) or, udv=(cosx)(xdx)u
if u=x⇒du=dx, and
if dv=cosxdx⇒v=sinx
∫udv=∫xcosxdx
uv−∫vdu=xsinx−∫sinxdx=xsinx+cosx
- Eg: lnxdx
let u=lnx and dv=dx
lnxdx–∫udv=uv−∫vdu
=xlnx−∫dx=xlnx−x
- Eg: ∫x2exdx=x2ex−2∫xexdx
=x2ex−2(xex−∫ex)=x2ex−2(xex−ex)=(x2−2x+2)ex
- Partial fractions:
−1x−1+1x+1=−2x2−1
∫(−1x−1+1x+1)dx=−ln(x−1)+ln(x+1)+c
(It's not a coincidence that the two constants on top, -1 and +1, are opposite in sign but equal in absolute value.)
- Some example of impossible integrals:
- ∫e−x2dx(bell curve)
- ∫xxdx
- ∫sinxx
- ∫extanxdx
5. 積分技術:
- 積分不能函数の例
- Computer software can't say anything about a particular integra a all. that doesn't mean that the integral can't be done.
- Computer are stupid, and they may try brute-force techniques that fail because the computer runs out of memory or CPU time.
- E.g.: ∫dxx10000−1 can be done in closed form using, and it's not too hard for a proficient human to figure out how too attack it, but every computer program I've tried it on has failed silently.
>Top 6. Improper integrals:
- 6.1: Integrating a function that blows up:
- When we intergrate a function that blows up to infinity at some point in the interval, the result may be either finite or infinite.
- (>Fig.) The integral ∫10dxx2 is infinite, while ∫∞1dxx2 is finite.
- Eg: Newton's law of grvity: the gravitational force between two objects is given by
F=Gm1m2r2. Compute the work that must be done to take an object from the earth's surface, at r=a, and revove it to r=∞.
- W=∫∞aGm1m2r2dr=Gm1m2∫∞af−2dr=−Gm1m2[r−1]∞a=Gm1m2a
- 6.2: ¶ Newton's law of gravity: the gravitational force between two objects is given by:
- F=Gm1m2r2, where G is a constant, m1 and m2 are the objects' masses, and r is the center-to-center distance between them.
- The work to be done form the surface r=q to r=∞:
W=∫∞aGm1m2r2dr=−Gm1m2r−1|∞a=Gm1m2a
6. 広義積分:
- Improper integration:
∫∞1dxx2
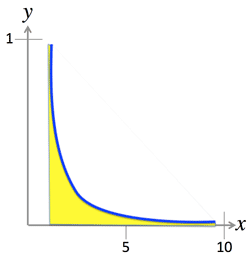
>Top7. Sequences and Series:
- 7.1: Infinite sequences:
- f(n)=nn+1; coverging to 1
- 7.2: Infinite series: sum of infiniely many numbers, refered to as an infinte series.
- ∑∞n=012n
- We can define a sequence of the partial sums 1,1+x,1+x+x2,....
We can then define convergence and limits of series in terms of convergence and limits of the partial sums.
- 7.3: Tests for convergence:
- Bounded and increasing sequences:
A sequence that always increase, but never surpasses a cnertain value, converges.
- Alternating series with terms approaching zero:
- the integral test:
- Eg: ∑∞n=11n
- The interal of 1x is lnx, which diverges as
x appraches infinity, so the series diverges as well.
- The ratio test:
- If the limt R=limn→∞|an+1an| exits,
then the sum an converges if R<1 and diverges if R>1.
7. 数列と級数:
- 7.1: 無限数列
- 7.2: 無限級数
- 7.4: テーラー展開:
- There is a cycle of sine, cos, -sin, and -cos, repeating indefinitely. Evaluating these derivatives at x=0,
we have 0, 1, 0, -1, ...
All the even-order terms of the series are zero,
and all the odd-order terms are ±1n!:
sinx=x−13!x3+15!x5−....
The
liner term is the familiar small angle approximation
sinx≈x.
- Taylor series of lnx,
evaluated around x=1,(f(x)=lnx):
f′(x)=x−1,f″(x)=−x−2,f‴(x)=2x−3,f⁗(x)=−6x−4,...
(NB: lnxblows up to negative infinity at x=0.
Coefficient of the Taylor series are ±(n−1)!n!=±1n
lnx=(x−1)−12(x−1)2+13(x−1)3+...
- 0!=1 has a sense:
4!=5!5,3!=4!4,...0!=1!1=1
- The function ex and the tangent line at x=0:
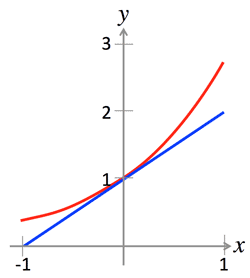
>Top Taylor series:
- Tc(x)=∑∞n=0an(x−c)n,where,
an=1n!dnydxn|x=c
- Eg: Find the Taylor series of lnx, evaluated around x=1
- ddxlnx=x−1
- d2dx2lnx=−x−2
- d3dx3lnx=2x−3
- d4dx4lnx=−6x−4
- lnx blows up to negative infinity at x=0.
- at x=1, we find that the nth derivative equals ±(n−1)!, so the coefficients of the Taylor series are
±(n−1)!n!=±1n.
- The resulting series is
lnx=(x−1)−12(x−1)2+13(x−1)3+...
- Maclaurin's theorem:
f(x)=f(0)+f′(0)1!x+f″(0)2!x2+...+f(n−1)(0)(n−1)!xn−1+fnθxn!xn,0<θ<1
- ex=1+x1!+x22!+...+xn−1(n−1)!+Rn,Rn=eθxxnn!
- sinx=x−x33!+x55!−...+(−1)n−1x2n−1(2n−1)!+R2n+1,R2n+1=(−1)ncosθx(2n+1)!x2n+1
- cosx=1−x22!+x44!−...+(−1)nx2n(2n)!+R2n+2,R2n+2=(−1)n+1cosθx(2n+2)!x2n+2
- log(1+x)=x−x22+x33−...+(−1)nxn−1n−1+Rn,Rn=(−1)n+1xnn(1+θx)n
- Binominal Theorem:
let \binom{\alpha}{k}=\frac{\alpha(\alpha-1)...(\alpha-k+1)}{k!}
(1+x)^{\alpha}=1+\binom{\alpha}{1}x+\binom{\alpha}{2}x^2+...+
\binom{\alpha}{n-1}x^{n-1}+R_n,
R_n=\binom{\alpha}{n}(1+\theta x)^{\alpha-n}x^n
>Top The Basel problem (of Euler):
- 1+\frac{1}{2^2}+\frac{1}{3^2}+...=\frac{\pi^2}{6}
- Using Tayor series, \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ ...
- Dividing throught by x; \frac{\sin x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+ ...
- Using Weierstrass factorization theorem; the left side if the product of liner factors given by its roots;
\frac{\sin x}{x}=(1-\frac{x}{\pi})(1+\frac{x}{\pi})(1-\frac{x}{2\pi})(1+\frac{x}{2\pi})(1-\frac{x}{3\pi})(1+\frac{x}{3\pi})...
=(1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})(1-\frac{x^2}{9\pi^2})...
- The x^2 coefficient of \frac{\sin x}{x} is
-(\frac{1}{\pi^2}+\frac{1}{4\pi^2}+\frac{1}{9\pi^2}+ ...)=-\frac{1}{\pi^2}\displaystyle\sum_{n=1}^\infty\frac{1}{n^2};
- From the oritian infinite series expansion of \frac{\sin x}{x}, the coefficient of x^2 is -\frac{1}{3!}=-\frac{1}{6}
- Multiplying both side of the equation by -\pi^2 gives: \displaystyle\sum_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}
>Top 8. Complex number techniques:
- 8.1: Review of complex numbers:
- 8.2: Euler's formula: denoted as "cis(x), the most remarkable formula in mathematics".
- f(x)=(\cos x-i\sin x)e^{ix}\\
f'(x)=(-\sin x-i\cos x)e^{ix}+(\cos x-i\sin xie^{ix})
=0\\
\therefore f(x)=c\\
f(0)=1
\Rightarrow \; (\cos x-i\sin x)e^{ix}=1\\
e^{ix}=\cos x+i\sin x
- \int e^x\cos xdx=\int e^x(\frac{e^{ix}+e^{-ix}}{2})\\
=\frac{1}{2}\int (e^{(1+i)x}+e^{(1-i)x})dx\\
=\frac{1}{2}(\frac{e^{(1+i)x}}{1+i}+\frac{c^{(1-i)x}}{1-i})+c
- Complex number and its complex conjugate:
- z=x+iy=|z|(\cos{\phi}+i\sin{\phi})=re^{i\phi}
- z=x-iy=|z|(\cos{\phi}-i\sin{\phi})=re^{-i\phi}
where
x=\mathrm{Re}\{z\} the real part
y=\mathrm{Im}\{z\}
the imaginary part
r=|z|=\sqrt{x^2+y^2} the magnitude of z
\phi =\mathrm{arg}z=\tan^{-1}(\frac{y}{x})
- Logarithm of complex number:
- a=e^{\ln{(a)}}
e^ae^b=e^{a+b} both valid for any complex numbers a and b.
- z=|z|e^{i\phi}=e^{\ln{|z|}}e^{i\phi}=e^{\ln{|z|}+i\phi}
\ln{z}=\ln{|z|}+i\phi
- (e^a)^k=e^{ak} de Moivre's formula
- Relationship to trigonometry:
- e^{ix}=\cos x+i\sin x \\
e^{-ex}=\cos x-i\sin x
- \cos x=\mathrm{Re}\{e^{ix}\}=\frac{e^{ix}+e^{-ix}}{2}\\
\sin x=\mathrm{Im}\{e^{ix}\}=\frac{e^{ix}-e^{-ix}}{2}
- letting x=iy, we have:
\cos{(iy)}=\frac{e^{-y}+c^y}{2}=\cosh{(y)}
\\
\sin{(iy)}=\frac{e^{-y}-c^y}{2i}=i\sinh{(y)}
- MacLaurin expression:
- e^x=\displaystyle\sum_{n=0}^\infty\frac{x^n}{n!}
- \cos x=\displaystyle\sum_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}
- \sin x=\displaystyle\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1}
- Euler's formula: (x\Rightarrow ix)
- e^{ix}=\displaystyle\sum_{n=0}^\infty\frac{i^n}{n!}x^n
=\displaystyle\sum_{n=0}^\infty\frac{i^{2n}}{(2n)!}x^{2n}
+\displaystyle\sum_{n=0}^\infty\frac{i^{2n+1}}{(2n+1)!}x^{2n+1}
=\displaystyle\sum_{n=0}^\infty\frac{(-1)^n}{(2n)!}x^{2n}
+i\displaystyle\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1}
- \therefore e^{ix}=\cos x+i\sin x
8. 複素数技術:
- 8.2: Euler's formula (1748): d^{i\phi}:
,
- Johann Bernoulli noted:
\frac{1}{1+x^2}=
\frac{1}{2}(\frac{1}{1-ix}+\frac{1}{1+ix})
- and since
\int\frac{dx}{1+ax}=
\frac{1}{a}\ln{(1+ax)}+C
>Top 9. Iterated integrals:
- 9.1: Integrals inside integrals:
- In calculus an iterated integral is the result of applying integrals to a function of more than one variable (E.g.: f(x,y) or f(x,y,z))
- \int(\int f(x,y)dx)dy=\int\int f(x,y)dxdy
- The x integral has to be on the inside, and we have to do it first.
- 9.3: Polar coordinates:
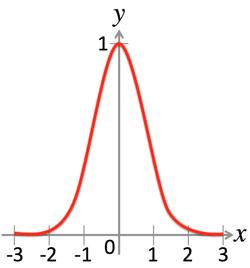
- Eg-99: Bell Curve known as the normal distribution (Gaussian) is shaped like e^{-x^2} (>Fig.)
- An area under this curve is proportional to the probability that x lies within a certain range.
- We need to evaluate
I=\int_{-\infty}^{\infty}e^{-x^2}dx
- the devious trick due to Poisson.
I^2=(\int_{-\infty}^{\infty}e^{-x^2}dx)(\int_{-\infty}^{\infty}e^{-y^2}dy)
I^2=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(e^{-y^2}e^{-x^2})dxdy
- I^2=\int_0^{2\pi}\int_0^{\infty}d^{-R^2}RdRd\phi=2\pi\int_0^{\infty}e^{-R^2}RdR
- Substitution u=R^2, du=2RdR, then
I^2=2\pi\int_0^{\infty}e^{-u}(\frac{du}{2})=\pi
\therefore I=\sqrt{\pi}
- 9.4: Spherical and cylindrical coordinates:
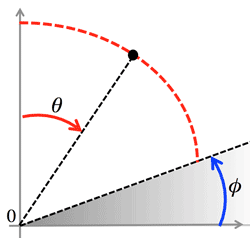
- In spherical coordinates (r, \theta, \phi); r measures the distance from the origin, and \theta and \phi are analogous to latitude and longitude, except that \theta is measured down from the pole.
- E.g.: the volume of a sphere.
V=\int dv \\
=\int_{\theta =0}^{\pi}\int_{r=0}^{r=b}\int_{\phi=0}^{2\pi}r^2\sin{\theta}d\phi dr d\theta \\
=2\pi\int_{\theta =0}^{\pi}\int_{r=0}^{r=b}r^2 \sin{\theta}dr d\theta \\
=2\pi \frac{b^3}{3}\int_{\theta =0}^{\pi}\sin{\theta}d\theta \\
=\frac{4\pi b^3}{3}
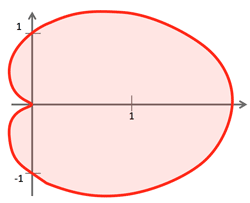
- Pascal's snail: (>Fig.) R=b(1+\cos{\theta})
- Quantifier: always immediately followed by a variable; suppose we want to say that a number greater than 1 exists;
There exists a number x such that x is greater than 1: \exists x \;x>1
- Quantifiers can be nested:
- \forall x \forall y \; x+y=y+x
- \forall x \exists y \; x+y=0
- \exists x \; x>1 \;\mathrm{as}\; \exists x\exists y\forall z \; yz=z\wedge x>y
9. 逐次積分:
- Bell Curve: e^{-x^2}
- Sperical coordinates:
- Pascal's snail:
>Top 10. xxxx:
10. xxxx:
Comment
- The concept of zero needed about 1000 years to be recognized its importance. Similarly that of infinitesimal and infinity needed about 200 years to be recognized of its importance.
- ゼロの概念はその重要性が認識されるまで千年かかった。同様に無限小や無限の概念もその重要性が認識されるまでほとんど200年かかった。
>Note |
Brief Calculus
|
Cat: SCI |
Benjamin Crowell |
16621u/18227r |
Title |
Brief Calculus |
簡単な微積分 |
|---|---|---|
Index |
||
Key |
; drivative; fluxions; hyperreal number; infinitesimal; polynominal; standard part; | |
Résumé |
Remarks |
>Top 1. Rate of change:
|
1. 変化率:
|
>Top 2. To infinity - and beyond!:
|
2. 無限、その先へ:
|
>Top3. Limits and continuity:
|
3. 極限値と連続:
|
>Top 4. Integration:
|
4. 積分:
|
>Top 5. Integration Techniques:
|
5. 積分技術:
|
>Top 6. Improper integrals:
|
6. 広義積分:
|
>Top7. Sequences and Series:
|
7. 数列と級数:
|
>Top Taylor series:
|
>Top The Basel problem (of Euler):
|
>Top 8. Complex number techniques:
|
8. 複素数技術:
,
|
>Top 9. Iterated integrals:
|
9. 逐次積分:
|
>Top 10. xxxx: |
10. xxxx: |
Comment |
|
|