Prime Obsession	Cat: SCI Pub: 2003 #:1009b
	John Derbyshire	10319u/18211r

Title	Prime Obsession	素数への執念
Index	Introduction: Card trick: The soil, the crop: The Prime Number Theorem: On the shoulders of giants: Riemann's Zeta Function: The great fusion: The Golden Key and an improved Prime Number Theorem: Not altogether unworthy: Domain stretching: A proof and a turning point: Nine Zulu Queens ruled China: Hilbert's eighth problem: The argument ant and the value ant: In the grip of an obsession: Big Oh and Möbius Mu: Climbing the critical line: A little algebra: Number Theory meets Quantum Mechanics: Turing the Golden Key: The Riemann operator and other approaches: The error term: Either it's true, or else it isn't:	序: カード・トリック: この土壌でこの収穫: 素数定理: 巨人たちの肩に乗って: リーマンのゼータ函数: 偉大な融合: 黄金の鍵と素数定理改良版: すべてが無価値とは限らず: 定義域の拡張: 証明と転換点: ９人のズールー族女王が中国を支配: ヒルベルトの第８問題: 変数アリとその価アリ: 執着に捕らわれて: ビッグオーとメビウスのミュー: 臨界線を上る: 代数をほんの少しだけ: 数論と量子力学の遭遇: 黄金の鍵を回す: リーマン演算子とその他アプローチ: 誤差項: 正しいか正しくないかいずれか:
Tag	; Abelian Function; Ad infinitum; Basel Problem; Carl F. Gauss; Complex function theory; Golden Key; Ligget se!; Number of primes; PNT (Prime Number Theorem); RH (Riemann Hypothesis); Sieve of Eratosthenes; Successor of Gauss; Transcendental number; Zeta Function; Zeta function graph; ;

Resume

要約

>Top 0. Introduction: How many prime numbers are there less than 20? The answer is eight; 2,3,5,7,11,13,17, and 19. How many are there less than one thousand? Less than one million? Less than one billion? Is there a general rule or formula for how many that will spare us the trouble of counting them? The Riemann Hypothesis is now stronger than ever since other great old open problems have been resolved in recent years: Four-Color Theorem: originated 1852, proved in 1976. Fermat's Last Theorem: originated in c1637, proved in 1994 The Riemann Hypothesis: "All non-trivial zeros of the zeta function have real part one-half."

0. 序章: 20より小さい素数はいくつあるか？答えは８個。2, 3, 5, 7, 11, 13, 17, 19である。 では1000より小さい素数の数は？では100万より小さい素数なら、10億より小さい素数なら... 個数を示す公式はあるのか？ リーマン予想への執着は、古くからある難問に最近答えがでたので、一層強くなっている。 四色問題：1852年出題、1976年解答 フェルマーの定理：1637年頃出題、1994年解答 リーマン予想とは: 「ゼータ函数の自明でない零点の実数部はすべて$\frac{1}{2}$である。」

>Top 1. Card trick: Take an ordinary deck of 52 cards. Now. with a finger slide the opmost card forward without moving any of the others. How far ca yuou slide it before it tips and falls? With that top card pushed out half its length over the second one, push theat second card with our findger How much compbined overhang can you get from these top two cards? The combined overhang is 3/4 of a card length. Now start pushing hte third card: the center of gravity is 1/6 of a card length back from the the leading edge of the the third card: $\frac{1}{6} + (\frac{1}{6}+\frac{1}{4}) + (\frac{1}{6}+ \frac{1}{4}+\frac{1}{2}) = 1+\frac{1}{2}$ If you keep going the overhangs accumulate like this for the 51 cards: $\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+ \frac{1}{10}+\frac{1}{12}+ ... +\frac{1}{102} = 2.25940659073334$ If there were a hundred cards, the total overhang would be: $\frac{1}{2} (1 +\frac{1}{2}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+ ... +\frac{1}{99}) = 2.58868875882$ If there wer a trillion card it would be: (a stack of a trillion playing cards would go most of the way from the earth to the moon.) $\frac{1}{2}(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+ ... +\frac{1}{999999999999}) = 14.10411839041479$ By adding enough terms of the harmonic series: the total has no limit: $(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+ ... )$ The harmonic series is divergent. The proof is rather easy. Nicole d'Oreame (14C) pointed out: $(\frac{1}{3}+\frac{1}{4}) >\frac{1}{2}$; so is $\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}$; so is $\frac{1}{9}+\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+ \frac{1}{13}+\frac{1}{14}+ \frac{1}{15}+\frac{1}{16}$; and so on. No matter how many blocks you take, the next block is well defined. There is always another on-half to be added; that means that the total increases without limit. Mathematicians are more interested in convergent series than divergent ones. But following series are convergent: $1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+ \frac{1}{32}+\frac{1}{64}+ ... = 2$ $1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}- \frac{1}{32}+\frac{1}{64}- ... =\frac{2}{3}$

1. カード・トリック: 52枚の普通のトランプカードを揃えて置く。一番上のカードをどの位前に押し出せるだろうか？ 1枚目のカードは半分の長さまでである。 2枚目のカードはさらに$\frac{1}{4}$で、合計$\frac{3}{4}$までせり出せる。 3枚目のカードは、さらに$\frac{1}{6}$までで、せり出した合計は、 $\frac{1}{6} + (\frac{1}{6}+\frac{1}{4}) + (\frac{1}{6}+\frac{1}{4}+ \frac{1}{2}) = 1+\frac{1}{2}$ 即ち、1.5倍で丁度三枚分の半分となる。 では、51枚のカードをせり出すとすれば $\frac{1}{2}+\frac{1}{4}+ \frac{1}{6} +\frac{1}{8}+\frac{1}{10}+ \frac{1}{12}+ ... +\frac{1}{102}\\ = 2.25940659073334$ もし、100枚のカードならば $\frac{1}{2}(1 +\frac{1}{2}+\frac{1}{4}+ \frac{1}{5}+\frac{1}{6}+ ... +\frac{1}{99})\\ = 2.58868875882$ もし、1兆枚のカードならば、 $\frac{1}{2}(1+\frac{1}{2} +\frac{1}{4} +\frac{1}{5}+\frac{1}{6}+ ... +\frac{1}{999999999999})\\ = 14.10411839041479$ 調和級数は発散する <左式> 但し、以下の級数は収斂する。 $1+\frac{1}{2}+\frac{1}{4}+ \frac{1}{8}+ \frac{1}{16}+\frac{1}{32}+ \frac{1}{64}+ ... = 2$ $1-\frac{1}{2}+\frac{1}{4}- \frac{1}{8}+ \frac{1}{16}-\frac{1}{32}+ \frac{1}{64}- ... =\frac{2}{3}$

>Top 2. The soil, the crop: Bernhard Riemann: we do no know much about him. He left no record of his inner life, other than what can be deduced from his letters. His friend Richard Dedekind wa the only person close to him who wrote a detailed memoir of 17 pages. Georg Friedrich Bernhard Riemann was born on Sept. 17, 1826 in the village of Breselenz of the Kingdom of Hanover. Riemann's father, Friedrich Berhard Riemann, was a Lutheran minister and a veteran of the wars against Napoleon. He was already middle-aged when he married Charlotte Ebell. Bernard was their second child and seems to have been especially close to his older sister Ida. Four more children followed, a boy and three girls. At the heart of the system was the 10-year gymnasium school (10-20 years). Riemann did not begin is proper schooling until age 14, four years into the gymnasium course. Riemann, aged 14, was terribly unhappy in Hanover, morbidly shy and homesick. Riemann does not seem to have been a good scholar. He had the type of mind that could hold only those things it found interesting, mathematics mostly. In 1846 he was admitted to the University of Göttingen as a student of theology. Göttingen was the only university within the sphere of the Hanover church. Göttingen did have one major attraction for the young Riemann. It was the home of Carl Friedrich Gauss, the greatest mathematician. Gauss was already 69 when Riemann arrived at Göttingen. We know that Riemann attended Gauss's lectures on linear algebra and those of Moritz Stern on the theory of equations. Outwardly he was pitiable; inwardly, he burned brighter than the sun. The purpose of the universities was conceived by their princely patrons as a place for the preparation of lawyers and physicians, teachers and preachers. >Top In 1849, Riemann began work in his doctorate, which he attained two years later, at 25, having submitted a dissertation on complex function theory. He became a lecturer at Göttingen three years after that and and associate professor in 1857. >Top The year 1857 was Riemann's breakout year. Riemann published a paper on analysis that was at once recognized to be a major contribution. Its title was "Theory of Abelian Functions." In it, he tackled topical problems by ingenious and innovative methods. In 1859, shortly before his 33rd birthday, Riemann was also appointed a correspoonding member of the Berlin Academy. The paper Riemann submitted to the Academy was titled "On the Number of Prime Numbers Less Than a Given Quantity." Mathematics has not been quite the same since.

2. この土壌でこの収穫: Bernhard Riemannについてはあまり知られていない。個人的な生活については、彼の手紙から推測する以外に何も残していない。 Richard Dedekindが、彼の唯一の友達であって17頁の回想録を残している。 Georg Friedrich Bernhard Riemannは、1826/9/17にハノーバー王国のBreselenzの村で生まれた。 Riemannの父は、Friedrich Berhard Riemannで、ルーテル派の牧師で、反ナポレオン戦争で参戦した経験があった。彼が中年になってから、Charlotte Ebellと結婚した。Bernardは彼らの第二子で、特に姉のIdaと親しかった。他に男１人、女3人の４人の兄弟がいた。 教育の中心は10年制のギムナジウム (10-20歳)であった。 リーマンが世紀の学校に入ったのは14歳の時で、 ギムナジウムのコースを４年過ぎていた。 14歳のRiemannにとっては、ハノーバーは楽しく所ではなく、病的なほど内気でホームシックだった。 リーマンは、優秀な生徒ではなかったようだが、自分の興味のあるものだけに熱心にやるタイプだった。それはほとんど数学だった。 1846年に、Göttingen大学の神学の学生として入学を認められた。Göttingenは、ハノーバー管内では唯一の大学だった。 Göttingenには、若いリーマンにとって最大の魅力があった。そこは偉大な数学者のCarl Friedrich Gaussの本拠だったのである リーマンは、ガウスの線形代数学やモーリッツ・シュテルンの方程式論の講義に出たことはわかっている。 彼は、外見から見るとみずぼらしかったが、内面では太陽よりも明るかった。 大学の目的は、それを援助する領主からは、法律家、医者、教師、牧師を養成する所であった。 1849年に、リーマンは博士論文を開始し、２年後の25歳の時に、複素函数論の論文を提出した。 彼は、3年後にGöttingenの講師となり、1857年には助教授となった。 1857年は、リーマンはブレイクした年となった。リーマンはすぐに大功績と認められる論文を出版した。そのタイトルは「アーベル函数理論」だった。その中で、当時話題の問題を巧みで創造的な方法で解いた。 1859年に、33歳になる直前に、リーマンはベルリン・アカデミーの客員会員に選ばれた。 リーマンがアカデミーに提出した論文のタイトルは「与えられた量よりも小さな素数の個数について」であった。これ以降、数学が変わっていくのである。

>Top 3. The prime number theorem (素数定理): There are 168 prime numbers up to 1,000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 173, 179, 181, 191, 193, 197, 199 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599 601, 607, 613, 617, 619, 631, 641 643, 647, 653, 659, 661, 673, 677, 683, 691 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997 How many primes less than N? >
>Top Between 1 and 100 there are 25 primes; between 401 and 500, 17; and between 901 and 1000, only 14. The number of primes in any block of 100 whole numbers seems to decline. Would we eventually reach a point beyond which there are no more primes; the biggest prime? Euclid (c300 BC) "The primes never thin out to nothing." Proof: Suppose N is a prime. Form this number; (1×2×3× ... ×N)+1 This number doesn't divide exactly by any number from 1 to N, you get remainder 1. So either it doesn't have any proper factors or its smallest proper factor is some number bigger than N.; Eg: (if $N$ is 5, then): 1×2×3×4×5 +1 =121 =11×11 The primes sure do thin out: (See the below) "Function" is one of the most important concepts in all of math, the second or third most important after "number" and possibly "set." A function is a way to turn (or 'map') a number into another number. $\pi (N)$ is defined to be the number of primes up to $N$. (The symbol $\pi$ is nothing whatsoever to circumference ratio.) The value of $\frac{N}{\pi (N)}$ go up by 7 each time. >Top The Prime Number Theorem (PNT): $\pi(N) \sim\frac{N}{\log N}$ $\frac{N}{\pi (N)}$ is close to $\log N$; and the larger $N$ gets, the closer (proportionally) it gets. The wavy line is properly called a tilde, or often called twiddle sign. If there are $\frac{N}{\log N}$ primes from 1 to N, the average density of primes in the range is $\frac{1}{\log N}$. Another way to say this is that in the neighborhood of a big number N, the probability of a number being prime is $\sim \frac{1}{\log N}$. We can estimate the size of the N-th prime. Consider a range of numbers from 1 to K, for some big number K. If the count of primes in the range is C, then on average we should expect to find the first of those numbers at $\frac{K}{C}$, the second at $\frac{2K}{C}$, the third at $\frac{3K}{C}$, and so on. The N-th will be around $\frac{NK}{C}$, and the C-th, which is to say the last in this range, will be around $\frac{CK}{C }= K$. Now, of the PNT is true, then the count C is actually $\frac{K}{log K}$, so that the N-th prime is actually around $\frac{NK}{\frac{K}{\log K}} = N \log K$. Since most numbers in this range resemble K in size, I can take K and N to be interchangeable, and the N-th prime is $\sim N \log N$. Eg: PNT predicts: the trillionth prime will be 27,631,021,1115,929; in fact, the trillionth prime is 30,019,171,804,121, 8% error. % erros at a thougsand, a million, and a billion are 13, 10, and 9. Consequences of the PNT: The probability that $N$ is prime is $\sim \frac{1}{\log N}$ The N-th prime number is $\sim N\log N$	1から100までの間に25個の素数があり、401から500まででは17個、901から1000の間は14個だけ。100毎の区分で素数の数は減少しているように見える。 ではある点より以降は素数はなくなるのか、つまり最大の素数はあるのか？ ユークリッドは、素数はまばらになるがなくならない。 証明：$N$を素数をする。(1×2×3× ... ×N)+1の数を作る。 この数は、1から$N$までのどの数でも割り切れず、１が余る。従って、この数には真の約数がないか、または、その最小の真の約数はNより大きな数であるかいずれかである。 例：1×2×3×4×5 +1 =121 =11×11 素数は確かにまばらになる。 函数は数学では、２番目か３番目に数や集合に次いで重要な概念である。 函数はある数を他の数に変換する (写像する)方法である。 $\pi (N)$ とは、$N$までの素数の数と定義される。 (ここでは円周率のπとは関係ない) $\frac{N}{\pi (N)}$の値は大体7倍になっている。 素数定理 (PNT): $\pi(N) \sim\frac{N}{\log N}$ $\frac{N}{\pi (N)}$ は、$\log N$に近い。$N$が大きくなると、それは比例的に近づく。〜はチルダ、またはニョロ。 もし1からNまでの間に$\frac{N}{\log N}$ 個の素数があれば、その範囲の素数の平均密度は$\frac{1}{\log N}$の値になる。 別の言い方では、大きなNの近辺では、素数になる確率は$\sim \frac{1}{\log N}$である。 同様にN番目の素数も推測できる。大きな数Kについて1からKまでの範囲を考える。 その範囲の素数の個数がCなら、平均的には、K/Cの所で最初の素数が見つかり、２番目は2K/C、３番目は3K/C、等々となる。N番目はNK/Cとなり、最後の素数であるC番目は、CK/C、即ち、Kの辺りにある。 さて素数定理が正しければ、個数Cは、実は$\frac{K}{log K}$のことであり、N番目の素数は、$\frac{NK}{\frac{K}{\log K}} = N \log K$辺りとなる。この範囲の数のほとんどはK位の大きさなので、KとNとは交換可能で、即ち、N番目の素数は、$\sim N \log N$となる。 素数定理による実例: 素数定理による予測では1兆番目辺りの素数は27, 631,021,115,929で、実際には1兆番目の素数は、30,019,171,804,121であり、誤差は8%である。千、百万、十億の場合のそれぞれの誤差は13%, 10%, 9%である。 素数定理の結論: Nが素数である確率: $\sim \frac{1}{\log N}$ N番目の素数は：$\sim N\log N$
>Top $\pi N$ $N$ Number of primes less than $N = \pi (N)$ $\frac{N}{\pi (N)}$ $\log N$ % error 1,000 168 5.9524 6.9077 16.0490 1,000,000 78,498 12.7392 13.8155 8.4487 1,000,000,000 50,847,534 19.6665 20.7232 5.3731 1,000,000,000,000 37,607,912,018 26.5901 27.6310 3.9146 1,000,000,000,000,000 29,844,570,422,669 33.6247 34.5387 2.7156 1,000,000,000,000,000,000 24,739,954,287,740,860 40.4209 41.4465 2.5386 Consequence of the PNT (The Prime Number Theorem): 素数定理からの結論: The probability that N is prime is $\sim \frac{1}{\log N}$ Nが素数である確率は$\sim \frac{1}{\log N}$ The N-th prime number is $\sim N\log N$ N番目の素数は$\sim N\log N$ Each of these results is equiponderant with (has the same weight as) the PNT. (これらは素数定理として同等)

>Top 4. On the shoulders of giants: The first person to whom the truth contained in PNT occurred was Carl Friedrich Gauss (1777-1855) Gauss came from extremely humble origins. His grandfather was a landless peasant; his farther was a jobbing gardener and brick layer. One day the schoolmaster, to give himself a half-hour break, set the class to adding up the first 100 numbers. Almost instantly, Gauss threw his slate onto the master's table, saying "Ligget se!" (There it is!) Carl Wilhelm, Duke truly was a gentlemen. Hearing of the boy Gauss's talent, the Duke asked to see him. He was sufficiently discerning that he took to the boy at once, remained his friend until death parted them, and provided the steady financial support that enables young Gauss to embark on a long brilliant career as a mathematician, physicist, and astronomer. Having lost his patron, Gauss had to find a job. He was offered and took, the position of director of the observatory at Göttingen University arriving there in late 1807. In the last 27 years of his life, he slept away from his beloved observatory only once, to attend a conference in Berlin. In December 1849 Gauss exchanged letters with the astronomer Johann Franz Encke. "The kind communication of your remarks about the frequency of primes was of interest to me as more than just a reference.... One of the first things I did was direct may attention to the decreasing frequency of primes, to which purpose I counted the same in several chiliads and jotted down the results on the attached white pages. I soon perceived that beneath all of its fluctuations, this frequency is, on average, close to inversely proportional with the logarithm."

4. 巨人たちの肩に乗って: 素数定理 (PNT)に含まれる真実を最初に発見したのはCarl Friedrich Gauss (1777-1855)である。 ガウスは極めて低い身分の出身である。祖父は小作農で、父は日雇い庭師や煉瓦職人であった。 ある日、先生が30分ほど休憩するために、生徒に100までの数を足しなさいと指示した。ほとんど瞬時に、ガウスは自分の石版を先生の机に持参して"リゲット・セ" (ほらできた)と言った。 Carl Wilhem公は実に紳士であった。ガウス少年の能力を聞くと、公は彼に会いに行った。彼は人を見る目があり、この少年を好きになると、その後生涯の友となり、ずっとガウスを庇護し、安定した支援を与えて、ガウスが数学者、物理学者、天文学者としての傑出した生涯を送れるようにした。 パトロンを失って、ガウスは仕事を探さねばならなかった。Göttingen大学の天文台所長の地位を得て、1807年末に赴任した。彼の人生の最後の27年間は、唯一度ベルリンでの会議出席を除いて、お気に入りのこの天文台以外で眠ることはなかった。 1849年12月に、ガウスは、天文学者のJohann Franz Enckeと手紙を交換した。 「素数の発生頻度に関するあなたの意見については一度の会議以上に興味があります。私が最初にしたことは、素数の頻度が減少することに注目したことでした。そのために千ずつ区切った区画毎に素数を数えて、その結果を何ページにも亘って書きました。変動はあるものの、平均的には、頻度は対数に反比例して近づいていくことに気づきました。」

>Top 5. Riemann's Zeta function: The Basel Problem: Find a closed form for the infinity series. $1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+...$ Mathematicians are not satisfied just to get an approximation, especially when the series under investigation converges rather slowly. They know from experience that getting that exact value often opens unexpected doors and throws light on the underlying math. The problem was finally cracked in 1735； 46 year after being posed, by the young Leonhard Euler; The astonishing answer was $\frac{\pi^2}{6}$. What is it doing in a question that has nothing to do with circle, or with geometry al all? The Basel problem opens the door to the zeta function, which is the mathematic object the Riemann Hypothesis is concerned with. It's as if log x were trying to be $x^0$. It is not $x^0$ (is defined to be 1). Even though log $x$ is not equal to $x^0$, it nonetheless manages to dip below, and stay below, $x^{\epsilon}$, for any number $\epsilon$, no matter how tiny, when $x$ is large enough. $1+\frac{1}{2^N}+\frac{1}{3^N}+\frac{1}{4^N}+\frac{1}{5^N}+...$ So long as N is an even number, Euler's result tells you the precise value, as c closed form, of the infinite series shown here: When N is 2, the series converges on $\frac{\pi^2}{6}$ When N is 4, it converges on $\frac{\pi^4}{90}$ When N is 6, it converges on $\frac{\pi^6}{945}$, and so on. When N is 26, it converges on $\frac{\pi^{26}}{11094481976030578125}$ What if N is odd: it is very difficult numbers. It was not until 1978 that N=3 of the series was even proved irrational >Top Zeta function: $\zeta (s) =\displaystyle \sum_{n}n^{-s} $ The function has values only when s is greater than 1. The domain of the zeta function is all numbers greater than 1. Right? Wrong!

5. リーマンのゼータ函数: バーゼル問題: 次の無限級数の閉じた形を求めよ。 $1+\frac{1}{2^2}+\frac{1}{3^2}+ \frac{1}{4^2}+\frac{1}{5^2}+...$ 数学者は近似では満足しない。収束が遅い場合は特に。経験上、正確な値が思わぬ扉を開き、根底にある数学に光りが当たることが多いからである。 この問題は46年後の1735年に解かれた。若き日のオイラーである。その恐るべき答は、$\frac{π^2}{6}$ である。(>証明は9. 参照) 円も幾何学も全く関係ない問題で、πが一体何をしているのだろうか バーゼル問題は、ゼータ函数の扉を開く。それはリーマン予想が関係する数学の対象である。 あたかも$\log x$ は $x^0$になろうとしているかのようである。もちろん$x^0$ (1と定義されている)ではない。$\log x$は$x^0$ではないが、ただ任意の$\epsilon$について、$\epsilon$がどんなに小さくとも、$x$が十分大きければ、$x^{\epsilon}$ よりも下に潜り込み、ずっとその下にいる Nが偶数であれば、オイラーの解は、閉じた形として左式の無限級数の正確な値を与える。 Nが2ならば、$\frac{\pi^2}{6}$に収束 Nが4ならば、$\frac{\pi^4}{90}$に収束 Nが6ならば、$\frac{\pi^6}{945}$に収束、以下同様 Nが26 ならば、以下に収束$\frac{\pi^{26}}{11094481976030578125}$ ではNが奇数の場合は、大変難しい数になる。1978年になって、N=3が無理数であることが証明された。 $\zeta$函数 <左式> この函数は $s$が1より大きい場合にのみ値を持つ $\zeta$函数の定義域は、1より大きなすべての数である。これは正しいか。実はそうではない！

>Top 6. The great fusion: Traditional categories of mathematics: Arithmetic: The study of whole numbers and fractions Geometry: The study of figures in space Algebra: The use of abstract symbols to represent mathematical objects (numbers, lines, matrices, transformations), and the study of the rules for combining those symbols. Analysis: The study of limits. Early 18C, analysis was still the newest and sexiest branch of math. Euler: Analysis is about infinite and infinitesimal. Modern counterpart: It is about limits and continuity. Greek Zeno: How an arrow moves?: If all time is composed of instants, and motion is not possible in any given instant, then how is motion possible at all? Irish philosopher George Berkely (17C): Evanescent increments are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities? Abstract simplicity: Language can represent complex ideas more easily: "A whale is big" Principia Mathematica takes 345 pages to define the number "1" Consider 2000-year struggle to domesticate the concept of "zero." Arithmetic:1 Arithmetic has the peculiar characteristic that it is rather easy to state problems in it that are ferociously difficult to prove. Goldbach's Conjuncture in 1742: Christian Goldbach put forward his famous conjuncture that every even number greater than 2 can be expressed as the sum of two primes. Fermat's Last Theorem Gauss: I confess that Fermat's Theorem has very little interest for me, because I could easily lay down a multitude of such propositions, which one could neither prove nor dispose of. >Top Ad infinitum: We can in imagination travel connectedly from any measuring number to any other, passing over the infinitude of other measuring numbers that lie between them, without ever finding ourselves without a number to stand on. Great mathematicians at work in 1800: Argand, Bolyai, Bolzano, Caucy, Fourier, Gauss, Germain, Lagrange, Laplace, Legendre, Monge, Poisson, Wallace. Gauss is the only German. Great mathematicians at work in 1900: Borel, Cantor, Carathéodory, Dedkind, Hadamard, Hrdy, Hilbert, Klein, Lebesgue, Mittag-Leffler, Poincarré, Volterra. 5 Germans Lejeune Dirichlet (born in 1805): Dirichlet married Rebecca Mendelssohn, one of sisters of the composer Felix Mendelssohn. "The Golden Key": inspired by a result Euler had proved 100 years before. 1837: brought together ideas from analysis and arithmetic to prove an important theorem about prime numbers. Proof of the theorem that each unlimited arithmetic progression whose first member and difference are whole numbers without common factor, contains infinitely many prime numbers. If you imagine each sequence stretching out to the neighborhood of some very large number N, then each contains about the same number of primes, about$\frac{\frac{N}{\log N}}{6}$: If N is 134, $\frac{\frac{N}{\log N}}{6}$ is about 4.55983336. Riemann's 1859 paper: he mentioned Dirichlet' name in conjunction with that of Gauss.

6. 偉大な融合: 数学の伝統的な分類: 算術：整数と分数の研究 幾何学：空間内にある図形の研究 数学的対象 (数、線、行列、変換)を表現するための抽象的な記号を用い、それらを組み合わせた規則の研究 解析学：極限の研究 18C初期、解析学は、数学の中でも最新の魅力ある分野であった。 オイラー：解析学は無限大と無限小の概念について 現代では：極限と連続性の概念について ギリシャのゼノン：飛ぶ矢は可能か？すべての時間は瞬間から成り、瞬間においては運動はあり得ない。ゆえに運動は可能だろうか？ アイルランドのGerge Berkely (17C): この儚い増分は有限の量でもなく、無限に小さい量でもなく、無でもない。それなら死んだ量の幽霊とでも呼ぶべきか？ 抽象的な単純性: 言語は複雑な概念を簡単に表現できる。例: "鯨は大きい" 数学原理は、1を定義するのに345頁を費やしている。 ゼロの概念をものにするには2000年間に亘る努力があった。 算術 算術には特異な性格がある。問題を表現するのは簡単だが、証明するのは極めて困難である。 ゴールドバッハの予想, 1742：2より大きな偶数は全て２つの素数の和として表される。 無限に (Ad infinitum): 我々は、想像の中では、どんな計量数から計量数へでも連結的に移動できる。その間の無念にある他の計量数を飛び越えて、かつ足を乗せる数字が見つからないということもなく。 1800に活躍していた数学者: アルガン、ボヤイ、ボルツァーノ、コーシー、フーリエ、ガウス、ジェルマン、ラグランジュ、ラプラス、スジャンドル、モンジュ、ポアソン、ウォレス ドイツ人はガウスのみ 1900年に活躍していた数学者: ボレル、カントール、カラテオドリ、デデキント、アダマール、ハーディ、ヒルベルト、クライン、ルベーグ、ミッタグ・レフラー、ポアンカレ、ヴォルテッラ 独５人 ディリクレ: メンデルスゾーンの妹の一人と結婚 "黄金の鍵": 100年前のオイラーの証明に触発を受ける。 1837：解析と算術の考え方をまとめた。 定理：公約数を持たない整数を初項と公差とする無限等差数列は、無限に多くの素数を含む どの数列も、大きなNの近傍については、素数定理が正しければ、どの数列もおよそ$\frac{\frac{N}{\log N}}{6}$個の素数がある。 もしNが134の場合には、$\frac{\frac{N}{\log N}}{6}$は約4.55983336 リーマンの1859年の論文：ディリクレの名がガウスの名と並んで挙げられている。

>Top 7. The golden key, and an improved prime number theorem: The Golden Key is, in fact, just a way that Leonhard Euler fround to express the sieve of Eratosthenes in the language of analysis. Top Sieve of Eratosthenes of Cyrene (around 230 BC), a small twon of now Libya: 2 - 3 - 5 - 7 - 9 - 11 - 13 - 15 - 17 - 19 - 21 - 23 - 25 - 27 - 29 - 31 - 33 - 35 - 37 - 39 - 41 - 43 - 45 - 47 - 49 - 51 - 53 - 55 - 57 - 59 - 61 - 63 - 65 - 67 - 69 - 71 - 73 - 75 - 77 - 79 - 81 - 83 - 85 - 87 - 89 - 91 - 93 - 95 - 97 - 99 101 - 103 - 105 - 107 - 109 - 111 - 113 If you stop just before process prime $p$, you have all the primes less than $p^2$. Since I stopped before processing 7, I have all the primes up to $7^2$, which is 49. I'm going to apply it to Riemann's zeta function, which I defined at Chapter 5.: $\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+ \frac{1}{5^s}+\frac{1}{6^s}+\frac{1}{7^s} ...$ $\frac{1}{2^s}\zeta(s)=1+\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{6^s}+ \frac{1}{8^s}+\frac{1}{10^s}+ ...$ $(1-\frac{1}{2^s})\zeta(s)=1+\frac{1}{3^s}+\frac{1}{5^s} +\frac{1}{7^s}+\frac{1}{9^s}+\frac{1}{11^s}+ ...$ $\frac{1}{3^s}(1-\frac{1}{2^s})\zeta(s)=\frac{1}{3^s}+\frac{1}{9^s} +\frac{1}{15^s}+\frac{1}{21^s}+\frac{1}{27^s}+ ...$ $(1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s)=1+\frac{1}{5^s}+ \frac{1}{7^s}+\frac{1}{11^s}+\frac{1}{13^s}+\frac{1}{17^s}+ ...$ $(1-\frac{1}{5^s})(1-\frac{1}{3^s})(1-\frac{1}{2^s})\zeta(s)=1+\frac{1}{7^s}+\frac{1}{11^s}+ \frac{1}{13^s}+\frac{1}{17^s}+\frac{1}{19^s} ...$ Notice the resemble to the sieve of Eratosthenes? Here, I eliminate the original prime from the right-hand side in the subtraction, along with all its multiples. So it is not too improbable to say that if you repeated the process forever, you'd get the result shown below: $...(1-\frac{1}{13^s})(1-\frac{1}{11^s})(1-\frac{1}{7^s})(1-\frac{1}{5^s}) (1-\frac{1}{3^s})(1\frac{1}{2^s})\zeta(s)=1$ (This is the Golden Key) Therefore, we can get more succinctly as: $\zeta(s)=\frac{1}{1-\frac{1}{2^s}} \frac{1}{1-\frac{1}{3^s}} \frac{1}{1-\frac{1}{5^s}} \frac{1}{1-\frac{1}{7^s}} \frac{1}{1-\frac{1}{11^s}} \frac{1}{1-\frac{1}{13^s}} ...$ A capital Greek letter $\Pi$, for product: "Zeta of $s$ equals the product over all primes of one minus $p$ to the minus $s$, to the minus one." The little p beneath the $\Pi$ sign is understood to mean over all primes." $\zeta(s)=\displaystyle\prod_p(1-p^{-s})^{-1}$ The Golden Key (or the Euler product formula, published in 1737) is: $\displaystyle\sum_n n^{-s}=\displaystyle\prod_p(1-p^{-s})^{-1}$ Both the sum on the left and the product on the right go all the way to infinity. This, in fact, offers another proof that the primes never end. Since it cannot be the case that an infinity on the left (the harmonic series) equals a finite number on the right, the number of primes must be infinite. Extremely impressive: The left side is an infinite sum through all positive whole numbers, while on the left side we have an infinite product through all the prime numbers. Euler's Latin: Si ex serie numerorum primorum sequens formetur expressio: (If from the series of prime number the following expression be formed:) $\frac{2^n3^n5^n7^n11^n...}{(2^n-1)(3^n-1)(5^n-1)(7^n-1)(11^n -1)...}$ erit eitus valor aequalis summae huius seriei (its value will be equal to the sum of this series...) $1+\frac{1}{2^n}+\frac{1}{3^n}+\frac{1}{4^n}+\frac{1}{5^n} +\frac{1}{7^n}+ ...$ 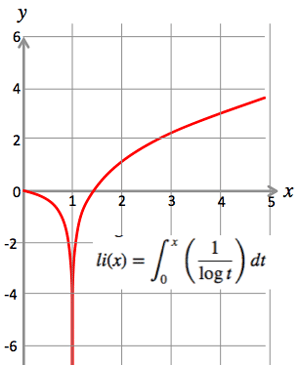Log integral function: $li(x)=\displaystyle\int_0^x\left(\frac{1}{\log t}\right)dt$

7. 黄金の鍵と改良版素数定理: 黄金の鍵は、要するにオイラーがエラトステネスの篩いを解析的に表現したものである。 エラトステネスの篩い(キュレネ、BC230頃): 113以下の篩いによる (左表) 素数pを処理する前の段階でやめれば、$p^2$より小さい素数はすべて入っている。 7を処理する前にやめれば、$7^2$つまり49より小さい素数はすべて得られている。 ここでリーマンのゼータ函数に当てはめると、１より大きなSについてのゼータ函数$\zeta(s)$は、左のようになる。 これの両辺を$\frac{1}{2^s}$倍すると左図のように無限個の和から分母に偶数の入っている項がすべて除かれる。 最初の式から第２の式を引く。 今度は両辺に$\frac{1}{3^s}$を掛ける 今度はこの式を一つ前の式から引くと無限個の和から、分母に3の倍数があるものがすべて消える。 これはエラトステネスの篩いの操作と類似している。 この手順を無限に繰り返すと、1より大きな$s$について、右辺は1に限りなく近づくといってよい。 これが黄金の鍵である。 $\prod$記号は、積を表す。$\prod$記号の下の$p$は"すべての素数について"という意味である。 左辺の和も右辺の積も、項の数は無限大である。これは素数に終わりがないことの証明である。左辺は、調和級数で、足すと無限大になるので、右辺も有限の数ではあり得ないので、素数の個数も無限大でなければならない。 左辺は全ての正の整数の和であり、右辺は全ての素数の積であるは極めて印象的。 Log integral function:

>Top 8. Not altogether unworthy: 1830s-1840s-1850s: the Romantic Movement; Paris remained the great center of mathematical research; Cauchy (1789-1857) and Fourier (1768-1830) had overhauled analysis; foundation of modern treatment to limits, continuity, and calculus. Berlin rising fast; Gauss (1777-1855); Dirchlet (1805-1859) in arithmetic, Jacobi in algebra, Steiner in geometry and Eisenstein in analysis. Bernhard Riemann (1826-1866) , 20 in 1847; doctorate course under Gauss, hoped to become a lecturer at Göttingen, but took 5 more years: Bernhard Riemann: From age 22.5 - 28; he had no income at all.; enrolled for in physics and philosophy. Dedekind (1831-1916), 19, five years younger than Remann, also aiming for a doctorate.; Riemann in 1851, and Dedekind in 1852, both were examined by Gauss (mid 70s; 1777-1855) Gauss gushed, "A substantial and valuable work, which does not merely meet the standards required for a doctoral dissertation, but far exceeds them." Nikolai Lobachevsky (1792-1856), inventor of non-Euclidean geometry; Pafnuty Chebyshev (1821-1894): "$\pi(N)$ cannot differ from $\frac{N}{\log N}$ by more than about 10% up or down. " James Styirling (Scottish); $N!\sim N^Ne^{-N}\sqrt{2\pi N}$ Joseph Bertrand postulate suggested in 1845; between any number and its double (e.g.: between 42 and 84) there is always a prime to be found. Chebyshev: if you divide a prime number (other than 2) by 4, the remainder must be either 1 or 3. Prime number /4 ... Remainder 1: 5, 13, 17, 29, 37, 41, 47, 59, 67, 71, 79, 83, (12 primes) Prime number /4 ... Remainder 3: 3, 7, 11, 19, 23, 31, 43, 53, 61, 73, 89, 97, 101 (13 primes) 1852: Dirichlet and Riemann met again and again. Immanuel Kant: "The Critique of Pure Reason"; Space is a pre-existing part of our mental equipment ... and it is necessarily Euclidean; The non-Euclidean geometry by Lobachevsky in 1830s was seen a philosophical heresy. Gauss had in fact invented non-Euclidean geometry for himself, but had not published his finding for fear. >Top Riemann became successor of Gauss in 1859; give a full professorship, then who gave the Academy his paper of "the number of primes less than a given quantity." In the paper, he acknowledge the two men; a subject which, through the interest shown in it by Gauss and Dirichlet over a long period, appears not altogether unworthy of such communication.

8. すべて無価値とは限らない: 素数定理 (Prime number theorem): 1792 by Gauss, 15 $\pi(x)\sim\text{Li}\: x \sim\frac{x}{\ln x}$ where, $\pi(x)$ is prime counting function, counting the number of prime numbers not more than $x$. $\Rightarrow \lim_{n\to\infty} \frac{\text{Li}\: x}{\pi(x)}=1$ $\text{Li}\:x=\displaystyle \int_2^x\frac{dt}{\ln t}$ $\Rightarrow \frac{\pi(x)}{x}\sim \frac{1}{\ln x}$

>Top 9. Domain stretching: The Riemann Hypothesis: All non-trivial zeors of the zeta function have real part one-half. If $s$ is some number bigger than 1, the zeta function is: $\zeta(s)=1+\frac{1}{2^s}+\frac{1}{3^s}+...+\frac{1}{n^s}+ ... = \displaystyle\sum_n n^{-s}$ by apply a pocess like the sieve of Eratosthenes to this sum: $\zeta(s)=\frac{1}{1-\frac{1}{2^s}}\frac{1}{1-\frac{1}{3^s}}\frac{1}{1-\frac{1}{4^s}}\frac{1}{1-\frac{1}{5^s}}\frac{1}{1-\frac{1}{6^s}}...=\displaystyle\prod_p(1-p^{-s})^{-1}$ Here is a diffrent infinite sum: $S(x)=1+x+x^2+x^3+x^4+x^5+...$ Value of the S(x) $x$ $S(x)$ $x\leq -1$ No value -0.5 0.666... -0.333... 0.75 0 1 0.333 1.5 0.5 2 $1\leq x$ No value Slightly different $\eta (s)$: $\eta (s)=1-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s} +\frac{1}{5^s}-....$ $\eta (s)=(1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+...)- 2(\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{6^s}+...)$ $\eta (s)=(1-2\frac{1}{2^s})\zeta (s)$ $\zeta (s)=\frac{\eta (s)}{(1-\frac{1}{2^{s-1}})}$

9. 領域の拡大: The Basel Problem: Taylor series: $f(x)$ that is infinitely diffrentiable at a real or complex number $a$ is: $f(a)+\frac{f'(a)}{1!}(x-a)+ \frac{f''(a)}{2!}(x-a)^2+\\ \frac{f'''(a)}{3!}(x-a)^3 +...=\\ \displaystyle\sum_{n=0} ^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n$ McLaurin expanson: $a=0$ $\sin x=\frac{x}{1!}-\frac{x^3}{3!}+ \frac{x^5}{5!}-...\\ +(-1)^{n-1}\frac{x^{2n-1}}{(2n-1)!}-...$ Euler's approach (*): $\sin(x)=x-\frac{x^3}{3!}+ \frac{x^5}{5!}-\frac{x^7}{7!}+...$ $\frac{\sin (x)}{x}=1-\frac{x^2}{3!}+ \frac{x^4}{5!}-\frac{7^2}{7!}+... $ Weirestrass factorization theorem: $\frac{\sin (x)}{x}=(1-\frac{x}{\pi}) (1+\frac{x}{\pi})\\ (1-\frac{x}{2\pi})(1+\frac{x}{2\pi})\\ (1-\frac{x}{3\pi})(1+\frac{x}{3\pi})...=\\ (1-\frac{x^2}{{\pi}^2})(1-\frac{x^2}{4{\pi}^2}) (1-\frac{x^2}{9{\pi}^2})...$ $x^2\;$coefficient should be equal (*): $-(\frac{1}{{\pi}^2}+ \frac{1}{4{\pi}^2}+ \frac{1}{9{\pi}^2}+... )=\\ -\frac{1}{{\pi}^2}\displaystyle\sum _{n=1}^{\infty}\frac{1}{n^2}$ $\therefore \; \displaystyle\sum _{n=1}^{\infty}\frac{1}{n^2}= \frac{{\pi}^2}{6}$

>Top 11. Nine Zulu queens ruled China: Graph of zeta function; every negative even number is a zero of the zeta function: $\zeta(-2)=0, \; \zeta(-4)=0, \; \zeta(-6)=0, \;$ and so on. Unfortunately, all those negative even numbers are trivial zeros. So... where are these nontrivial ones? Complex numbers seem scary or fantastic, or impossible; they are no more imaginary than any other kind of number. $\mathbb{N}, \;\mathbb{Z}, \;\mathbb{Q}, \;\mathbb{R}, \;\mathbb{C}, \; $ "Nine Zulu Queens Ruled China."; like matryoshka doll. Innermost doll; Natural numbers 1, 2, 3, 4, ... Next doll; Integers: Natural numbers + 0 + negative numbers Next doll; Rational numbers; together with all positive and negative fractions (proper fractions and improper fractions (vulgar or mixed improper fractions) Next doll; Real number; together with irrational number like $\sqrt{2}, \pi, e$ (closed forms like $\sqrt[5]{7+\sqrt{2}}, \frac{{\pi}^2}{6}$) Outermost doll; Complex numbers $\mathbb{P}\;$ Prime numbers are a subset of $\mathbb{N}$ $\mathbb{A}\;$ Algebraic number is a important subset of $\mathbb{C}$, and a number that is a zero of some polynominal with coefficients all in $\mathbb{Z}.$ An irrational number might or might not be algebraic. Those that are not are called transcendental. Complex numbers are wonderful; can even raise them to complex powers: $(-7-4i)^{-2+5i}$ is approximately -7611.97...+206.35 .. i In 1874: Georg Cantor had shown; ;$\mathbb{R}$ is infinite, and the number of irrational numbers is infinite, but the second infinity is bigger than the first. Complex plane in action: $\frac{1}{1-x}=1+x+x^2+x^3+x^4+... \; (-1<x<1)$ Does this work for complex numbers? $(x=\frac{1}{2}i)$ $\frac{1}{1-\frac{1}{2}i}=1+\frac{1}{2}i+\frac{1}{2^2}i^2+ \frac{1}{2^3}i3+\frac{1}{2^4}i4+...$ $0.8+0.4i=1+\frac{1}{2}i-\frac{1}{2^2}-\frac{1}{2^3}i+ \frac{1}{2^4}+\frac{1}{2^5}i-...$ On the complex plane, start at the point 1, then go north to $\frac{1}{2}i$, then to west $\frac{1}{4}$; then go south $\frac{1}{8}i$ ... and so on. ; a neat spiral closing to $0.8+0.4i$

11. ９人のズールー族女王が中国を支配: Transcendental number (超越数): a real or complex number that is not algebraic (not a root of a non-zero polynomial equation with rational coefficients. extremely difficult to show the given number is transcendental. transcendental numbers are not rare; indeed, almost all real and complex numbers are transcendental. (algebraic numbers are countable, while real and complex numbers are both uncountable.) all real transcendental numbers are irrational, since all rational numbers are algebraic. The converse is not true. ($\sqrt{2}$ is irrational but not transcendental. $e \;$ is proven transcendental by Charles Hermite in 1873. $\pi \;$ is proven transcendental by Ferdinand von Lindermann in 1882. 1874: Georg Cantor proved that algebraic number is countable and real numbers are uncountable, and proved as many transcendental numbers as there are real numbers (diagonal argument; ubiquity of transcendental numbers). $e^{i\pi}=-1$ is algebraic (Euler's identity) is is unknown whether $\pi +e$ is transcendental, though at least one of $\pi +e$ and $\pi e$ must be transcendental. ....

>Top 12. Hilbert's eighth problem: Existence proof: David Hilbert (1862-1943) had proved that the objects exist but had not produced them. "There is at least one student in this class - let us name him X. No other student is the class has more hairs on his head than X. Which student is it? that we shall never know; but of his existence we can be absolute certain." Important mathematicians and physicists of the first half of 20C had studied either at Göttinggen , or under someone who had studied there. Hilbert 23 Problems in mathematics: Aug. 8, 1900 at the Second International Congress of Mathematicians; Hilbert ended with a list of 23 particular problems "from the discussion of which an advancement of science may be expected." Hilbert was a man who did not suffer fools gladly and that he classed rather a large part of humanity as fools; this was particularly unfortunate in Gukbert's case; because Franz, his only child, was afflicted with serious mental problems. 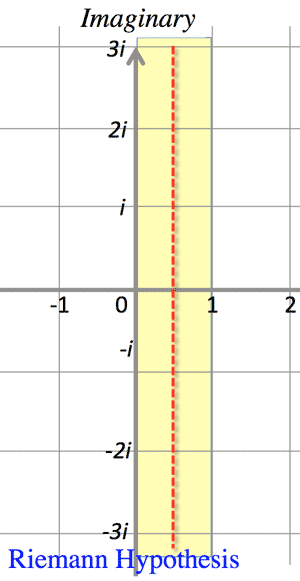The Riemann Hypothesis (stated geometrically) Using the complex plane to visualize this, non-trivial zeros are now to lie in the critical strip. The Riemann Hypothesis makes a stronger assertion, that they all lie on the line whose real part if $\frac{1}{2}$: Critical strip and critical line are common terms of art in discussion of the Riemann Hypothesis: "All nontrivial zeros of the zeta function lie on the critical line." The zeros occur in conjugate pairs. if $z=a+bi=0$, then $\bar z=a-bi=0$ 20C was a very ... busy century. The story of the Riemann Hypothesis in 20C is not a single linear narrative, but a number of threads, sometimes crossing, sometimes tangling with each other. How mathematics developed from 1900-2000: Most of 19C math was concerned with numbers; whole numbers, rational numbers, real numbers, complex numbers. New mathematical objects were created; functions, spaces, matrices - and powerful new tools devised for the manipulation of these objects. A typical product of 20C was "functional analysis", where the fundamental object of study is sequences of functions, which might or might not converge. Mathematics is a cumulative subject. Every new discovery adds to the body of knowledge, and nothing is ever subtracted. It never becomes untrue or irrelevant - though it might become unfashionable, or as a particular case of some more general theory. In mathematics, more general does not necessarily mean more difficult. 1903; Danish mathematician Jorgen Gram had shown the zeros: $\frac{1}{2}+14.134725i, \frac{1}{2}+21.022040i, \frac{1}{2}+25.010856i , ...$ Their real prts were centainly one-half, as Riemann had hypothesized, but the imaginary parts showed no apparent order or pattern.

12. ヒルベルトの第８問題: 高木貞治(1875-1960)はGøitting大学でのHilbeltの弟子 The Riemann Hypothesis (stated geometrically): <Fig-1>

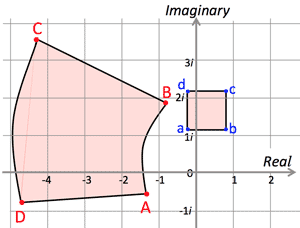
>Top 13. The argument ant and the value ant: <Fig-2> shows a square (abcd) in the complex plane: $a=-0.2+1.2i, \; b=0.8+1.2i, \; c=0.8+2.2i, \; d=-0.2+2.2i$ Squaring funcion stretches the sheet counter-clokwise round the zero point, while simultaneously stretching it outward from that point for the nmbers shown.: $A=-1.4-0.48i, \; B=-0.8+1.92i, \; C=-4.2+3.52i, \; D=-4.8-0.88i$ The figure helps with complex functions to think of the complex plane as an infinitely stretchable sheet of rubber and ask what a function does to this sheet. >Top Zeta function graph: $\zeta(s), \; (s<1)$ Riemann had a very powerful visual imagination; the graph contains some powerful results and gives deep insights into the behavior of complete functions, also yokes function theory to algebra and topology, two key growth areas of 20C math. <Fig-3>: "sent to" diagram: When $x-0, \zeta(s)=\frac{1}{2},$ at $s=-2$, the curve crosses the $s$-axis, that is, $\zeta=0.$ It then climbs up to a modest height (actually 0.009159890... before turning down and crossing the axis again at $s=-4.$ The graph drops down to a shallow trough (-0.003986441...) before rising again to cross the axis at $s=-8$, a slightly deeper trough (-0.007850880...), across the axis at -10, now a really noticeable peak (0.022730748...), across the axis at $s=-12$, a deep trough (-0.093717308...), across the axis at $s=-14$, and so n. 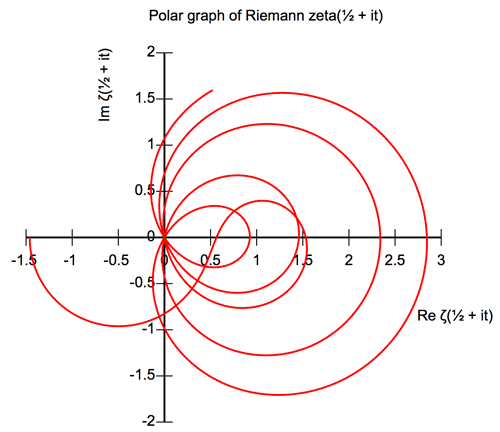<Fig-4>: "comes from" diagram: Now suppose that the argument ant takes a walk straight up the critical line (of Fig-1) , heading due north from argument $\frac{1}{2}$. What path will the value ant follow? His path starts out at $\zeta(\frac{1}{2})$, which is -1.44603545088095... then he does a sort of half-circle counterclockwise below the zero point, then turns and loops clockwise around 1. He heads to zero and passes through it (passed $\frac{1}{2}+14.134725i).$ Then, he keeps going round in clockwise loops, passing trough the zero point every so often - whenever his twin on the argument plane steps on a zero of the zeta function. I stopped his walk when the argument ant reached $\frac{1}{2}+35i$. By that point, the curve has passed through zero five times, corresponding to the five non-trivial zeros. Notice that points on the critical line have a strong tendency to map to points with positive real part.

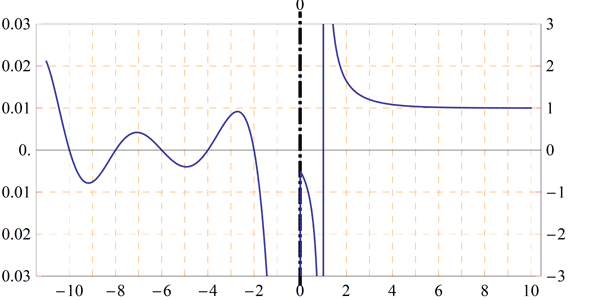
13. 変数アリとその価アリ: Squaring of complex number: <Fig.-2> the argument plane & the value plane. Zeta function: "Sent to diagram"<Fig-3> Zeta function: "Comes from diagram"<Fig-4>

>Top 14. In the grip of an obsession: Göttingen was not the only place where first-class mathematics was being done int the early 20C. John Edensor Littlewood, 1885-1977, Trinity College, Cambridge, in 1907.; Isaa Newton's college, 1661-1693 Godfrey Harold Hardy, 1877-1947 Edmund Landau, 1877-1938 George Boole Paris Congress, 1900: France 90, Germanry 25, US 17, Italy 15, Belgium 13, Russia 9, Austria 8, Swizerland 8, UK 7: US in 1900 was a back water. Hardy and Littlewood becmae infected withte R.H. obsession. Hardy's 1914 result: Infinitely many of the zeta function's non-trivail zeros satisfy the R.H. - that is, have real part one-half. Though, this leaves three possibilities sitll open: Infinitely many zeros do no have real par one-half. Only finitely many zeors do no have real part one-half. There are no zeors that do no have real part one-half.

14. 執着に捕らわれて: Nowadays, there are only thress really great English mathematicians: Hardy, Littlewood, and Hardy-Littlewood.

>Top Acutual values of the erro term: Relative error is certinly dwindling away to zero. Littlewood's 1914 paper came as a sensation, for it proved that this is not so; on the contray, there are numbers $x$ for which $\pi (x)$ is greater than $Li(x)$. (Crossover point) Samuel Skewes showd that if R.H. is true, the crossover point must come before $e^{e^{e^{79}}}$ (Skewes' number) Number of all atoms in the cosmos: $\sim 10^{80}$ In 1966, Sherman Lehman pulled the upper bound down to a much more manageable figure: 1.165×$10^{370}$ In 2000, the best fireure is established by Cartey Bays and Richard Hudson; 1.39822×$10^{316}$, mentioning a small possibility of lower violations maight exist as low as $10^{176}$, and a huze zone of violation around 1.617×$10^{9608}$ In 1911Helge von Koch had proved the following key result: If the R.H. is true, then $\pi (x)=Li(x)+O(\sqrt{x}\log x)$ N: $x$ Number of primes less than N: $\pi (x)$ Error Term Aboslute $Li(x)-\pi (x)$ Relative: Absolute / $\pi (x)$ 1,000 168 10 0.0595 2380 9524 1,000,000 78,498 130 0.0016 5609 3149 1,000,000,000 50,847,534 1,701 0.0000 3345 2950 1,000,000,000,000 37,607,912,018 38,263 0.0000 0101 7419 1,000,000,000,000,000 29,844,570,422,669 1,052,619 0.0000 0003 5270 1,000,000,000,000,000,000 24,739,954,287,740,860 21,949,555 0.0000 0000 0887

>Top 15. Big Oh and Mörbius Mu: Paul Turán: Definition of Big Oh: Function $A$ is big oh of function $B$ if, for large enough arguments, the size of $A$ nver exceeds some fixed multiple of $B$. $\log x$ grows more slowly than any positive power of $x$; this can be expressed using bigh-oh notation thus: $\log x=O(x^{\epsilon}).$ Koch's error tierm= $O(\sqrt{x}\log x)$ implies "Error tierm = $O(x^{\frac{1}{2}+\epsilon})$"; but the converse is not true. >Top Take the Golden Key and trun it upside down: $\frac{1}{\zeta(s)}=(1-\frac{1}{2^s})(1-\frac{1}{3^s})(1-\frac{1}{5^s})(1-\frac{1}{7^s})(1-\frac{1}{11^s})(1-\frac{1}{13^s})...$ First term: whose value is just 1. Second term: Plunk the 1 from every parenthesis except the first. From the one, pluck the $-\frac{1}{2^s}$. This gives the infinite product, which is just $-\frac{1}{2^s}$ Third term: Plunk the 1 from every parenthesis except the second. From the one, pluck the $-\frac{1}{3^s}$. This gives the infinite product, which is just $-\frac{1}{3^s}$ Fourth term: Plunk the 1 from every parenthesis except the nth, whose term equals to $-\frac{1}{p^s}$, where $p$ is the nth prime. So the infinite sum looks like as follows: $1-\frac{1}{2^s}-\frac{1}{3^s}-\frac{1}{5^s}-\frac{1}{7^s}-\frac{1}{11^s}-\frac{1}{13^s}...$ Suppose I pluck $-\frac{1}{2^s} from the first parenthesis, $-\frac{1}{3^s}$ from the second, and 1 from all the others. This gives: $(-\frac{1}{2^s}×(-\frac{1}{3^s})×1×1×....), which is $\frac{1}{6^s}.$ I shall get a similar term from every possible pair of not-1 plucks. Plucking $-\frac{1}{5^s}$ from the third parentheis, $-\frac{1}{13^s}$ from the sixeth, and 1 from every others, give a term $\frac{1}{65^s}.$ $1-\frac{1}{2^s}-\frac{1}{3^s}-\frac{1}{5^s}-\frac{1}{7^s}-\frac{1}{11^s}-\frac{1}{13^s}-...$ $+\frac{1}{6^s}+\frac{1}{10^s}+\frac{1}{14^s}+\frac{1}{15^s}+ \frac{1}{21^s}+\frac{1}{22^s}+\frac{1}{26^s}+\frac{1}{33^s}+...$ The next step is to take all possible plucks of three not-1s, with all other plucks equal to 1. Assuming to keep doing this, and rearrange the resulting terms at will, the result boils down to: $\frac{1}{\zeta (s)}=1-\frac{1}{2^s}-\frac{1}{3^s}-\frac{1}{5^s}+\frac{1}{6^s}-\frac{1}{7^s}+ \frac{1}{10^s}-\frac{1}{11^s}-\frac{1}{13^s}+\frac{1}{14^s}+\frac{1}{15^s}-... $ Möbius function, named after August Ferdinand Möbius (1790-1868): $\mu (n)$: Its domain is $\mathbb{N}$, all natural number 1, 2, 3, ... $\mu (1)=1$ $\mu (n)=0$ if $n$ has a square factor. $\mu (n)=-1$ if $n$ is a prime, or the product of an odd number of diffrent primes. $\mu (n)=1$ if $n$ is the product of an even number of different primes. Möbius function is tremendously useful in the theory of numbrers; boil down to the following elegant result: $\frac{1}{\zeta(s)}=\displaystyle\sum_n \frac{\mu (n)}{n^s}$ Merten's function: $M(k)=\mu (1)+\mu (2)+\mu (3)+...\mu (k)$ the first 10 values; 1, 0, -1, -1, -2, -1, -2, -2, -2, -1 (oscillating back and forth around zero just like a random walk.) for arguments 1000, 2000, ... up to 10000 it has the values; 2, 5, -6, -9, 2, 0, -25, -1, 1, -23 for argument 1 million, 2 million, ... up to 10 million it has values: 212, -247, 107, 192, -709, 257, -184, -189, -340, 1037 (the size of M(k) increases) If the following Theorem is true, the Hypothesis is true, and if it is false, the Hypothesis is false: $M(k)=O(k^{\frac{1}{2}})\;$ (this is stronger than the Hypothesis) $M(k)=O(k^{\frac{1}{2}+e})\;$ (this is slightly weaker version)

15. ビッグ・オーとメビウスのミュー:

>Top 16. Climbing the critical line: Sept. 8, 1930: David Hilbert: "Wir müssen wissen, wir werden wissen." (We must know, we shall know.) Horrors engulfed Germany in early 1933: Enabling Act of Mar. 23: Edmund Landau (1877-1839), Richard Courant, Felix Bernstein were Jewish.

16. 臨界線を上る:

>Top 17. A little algebra: Field theory and Operator theory: Here is a mathematical object, the Hermitian matrix, which is built up of complex numbers; the list of its eigenvalues consists entirely and unexpectedly of real numbers. Now here is a function, the Riemann zeta function, which is built up of complex numbers; and its most intimate and essential property is the list of its non-trivial zeros. Every one of these zeros is in the critical strip. They are symmetrical about the critical line, whose real part is $\frac{1}{2}. Let's say a typical zero is $\frac{1}{2}+zi$, for some number $z$. Then the Riemann Hypothesis says that all the $z$'s are real. The Hilbert-Pólya Conjecture: The non-trivial zeros of the Riemann zeta function correspond to the eigenvalues of some Hermitian operator.

17. 代数をほんの少しだけ:

>Top 18. Number theory meets quantum mechanics: Spring of 1972 serendipity; at Princeton's Institute for Advanced Study. The number theorist was Hugh Montgomery, a young American doing graduate work at Trinity College, Cambridge. The physicist was Freeman Dyson, a renowned physicist. The expression that had emerged from his inquiries into the Riemann zeta function's non-trivial zeros, was precisely the form factor associated with a random Hermitian matrix - the kind of thing Dyson had been involved with for seral years in his researches into quantum dynamic systems. I took afternoon tea that day in Fuld Hall with Chowla. Freeman Dyson was standing across the room. I had spent the previous year at the Institute and I knew him perfectly well by sight, but I had never spoken to him. Chowla said: "Have you met Dyson?" I said no, I hadn't. He said; "I'll introduce you." I said no, I didn't feel I had to meet Dyson. Chowla insisted, and so I was dragged reluctantly across the room to meet Dyson. He was very polite, and asked me what I was working on. I told him I was working on the differences between the non-trivial zeros of Riemann's zeta function, and that I had developed a conjecture that the distribution function for those differences has integrand $1-(\frac{\sin \pi u}{\pi u})^2$. He got very exited. He said; "That's the form factor for the pair correlation of eigenvalues of random Hermitian matrices!" I'd never herd the term "par correlation." It really made the connection. The next day Atle had a note Dyson had written to me giving references to Mehta's book, places I should look, and so on. to this day I've had one conversation with Dyson and one letter from him. It was very fruitful. I suppose by this time the connection would have been made, but it was certainly fortuitous that the connection came so quickly, because then when I wrote the paper for the proceedings of the conference, I was able to use the appropriate terminology and give the references and give the interpretation. I was amused when, a few years later, Dyson published a paper called "Missed Opportunities." I'm sure there are lots of missed opportunities, but this was a counterexample. It was real serendipity that I was able to encounter him at this crucial juncture. The Montgomery-Odyzko Law: The distribution of the spacings between successive non-trivial zeros of the Riemann zeta function (suitably normalized) is statistically identical with the distribution of eigenvalue spacings in a GUE operator. The non-trivial zeros of Riemann's zeta function arise from inquires into the distribution of prime numbers. The eigenvalues of a random Hermitian matrix arise from inquiries into the behavior of systems of subatomic particles under the laws of quantum mechanics. What on earth does the distribution of prime numbers have to do with the behavior of subatomic particles.?

18. 数論と量子力学の遭遇

>Top 19. Turning the golden key:

19. 金の鍵を回す:

>Top 20. The Riemann operator and other approaches:

20. リーマン演算子とその他のアプローチ:

>Top 21. The error term:

21. 誤差項:

>Top 22. Either It's true, or else it isn't:

22. 正しいか正しくないか、いずれか:

Comment

In mathematics, it is usually regular or random, or finite or infinite, ie. black or white world. But the prime number world seems random and regular, getting scarce and seemingly finite, but actually infinite. The prime world resembles in behavior of life: it looks like autonomous and randomly swinging individually, but looks quite restricted and regular macroscopically. It also resembles movement of distant galaxies: each star seems to move independently, but as a galaxy or galaxy cluster it seems to behave quite regularly.

数学では、通常は規則的かランダムか、または有限か無限かの白黒の世界が普通だが、素数の世界だけだは、ランダムでかつ規則的、稀薄になり、有限みたいだが無限という世界のようだ。 素数の世界は生命の振る舞いに似ている。それは個々には自律的でランダムに揺れているが、マクロ的には全く制限的で規則的に見える。 それはまた遠方銀河の動きに似ている。各々の星は個別に運動しているが、銀河あるいは銀河団としては、極めて規則的に振る舞っているように見える。