Summary |
要約 |
>Top
0. Prologue:
- Fermat's Last Theorem (FLT):
It is impossible to separate a cube into two
cubes, or a biquadrate into two biquadrates, or generally any power
except a square into two powers with the same exponent. I have discovered
a truly marvelous proof of this, which, however the margin is not
large enough to contain.
- Computers could verify the theorem for very large numbers
(billions of numbers) but they couldn't help for all numbers.
- Awards were offered in the 1800s by the French and German
scientific academies to anyone who would come up with a proof
- but always coming up empty-handed.
|
0. プロローグ:
- フェルマーの最終定理:
1つの立方数を2つの立方数に、また1つの四乗数を2つの四乗数に、さらに一般的に平方を除いて、いかなる乗数も1つの同一乗数に分けることはできない。私はこれを解く素晴らしい証明を発見したが、それを記すにはこの余白は十分ではない。
- コンピュータはこの非常に大きな何十億という数についてこの定理を証明したが、すべての数についての証明にはならなかった。
- 19Cに、仏と独の科学アカデミーが懸賞金を出したが、誰も証明に至らずいつも空振りで終わった。
|
>Top
1. Babylonian Era (2000-600 BC):
- Pythagorean triples: 52=32+42
- They were known to the Babylonian over 1000 years (around
1900 BC) before Pythagoras born around 580 BC.
- Clay tablet "Plimpton 322": contains 15 rows of
numbers, such as:
- 132=122+52
- 752=602+452
- 1692=1202+1192
- Note: where, m > n are natural numbers
m2+n2,2mn,m2−n2 are such numbers.
- The interest was solely for practical purposes, and the fact
that they used a number system with base sixty and therefore
preferred integers to fractions support this need to solved
practical problems with nice, whole square numbers.
- Number is everything:
Pythagoreans developed a substantial body of mathematical knowledge
all in complete secrecy.
- Perfect number: a number that is the sum of its multiplicative
factors.
- 6 = 3+2+1
- 28 = 14+7+4+2+1
- Pi (π): Pi was known to within various approximations to the
Babylonians and Egyptians of 2000s BC.
- Discovery of irrationality of the square root surprised and
shocked these diligent number admirers. They swore never to
tell anyone outside their society.
|
1. バビロニア時代 (2000-600 BC) :
- ピタゴラス3数:52=32+42
- それらは1000年以上も前 (約1900 BC)に、ピタゴラス (580 BC頃生) 以前に、バビロニア人によって知られていた。
- "Plimpton 322"という粘土板には15組のピタゴラス数が知られている。例えば
- 132=122+52
- 752=602+452
- 1692=1202+1192
- 注)m > n の自然数の場合、
m2+n2、2mn、m2−n2
はこの数になる。
- この興味は単に実用目的だったし、また60進法を使っていたので分数よりも整数を好んだという事実は、完全平方数に関する実際の問題をうまく解くための表を必要としたのだという。
- 万物は数である:
ピタゴラス派はすべて完全な秘密の内に重要な数学的知識を発展させた。
- 完全数: その約数の和になる数
- 6 = 3+2+1
- 28 = 14+7+4+2+1
- パイ(π) :2000 BC代にバビロニア人やエジプト人はπのさまざまな近似値を知っていた。
- 平方根という無理数の発見は勤勉な数の崇拝者達に驚きとショックを与えた。彼らは教団の外の誰にも口外しないと誓った。
|
-
>Top Georg Cantor (1845-1918):
- The numbers on the number line are of two district kinds rational
and irrational. The numbers are very, very close (infinitesimally
close) to each other.
- Any neighborhood around a rational number contains infinitely
many of these irrational numbers. And vice versa, around every
irrational numbers there are infinitely many rational ones.
- Both sets, the rational and the irrational numbers, are infinite.
But the irrational are so numerous that there are more of them
than there are rational numbers. Their order of infinity is
higher.
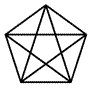 The
special symbol of the Pythagorean order was the five-pointed star
embedded in a pentagon. The
special symbol of the Pythagorean order was the five-pointed star
embedded in a pentagon.
- An important aspect of Pythagorean life was the pursuit of
philosophical and mathematical studies as a moral basis.
- A diagonal point divides a diagonal into two unequal parts:
This ratio is called the Golden Section. Irrational number 1:
1.618...
-
Tetraktys:
The Pythagoreans believed that all of heaven was musical scale
and 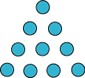 numbers. The basic ratio in music involved only the number
1,2,3, and 4, whose sum is 10. They considered the tetraktys holy
and even swore oaths by it. numbers. The basic ratio in music involved only the number
1,2,3, and 4, whose sum is 10. They considered the tetraktys holy
and even swore oaths by it.
|
-
ゲオルグ・カントール (1845-1918) :
- 数直線上の数は、有理数と無理数という2つの異なる種類の数からなる。数同士は互いにものすごく (無限小に)近接している。
- 一つの有理数の近傍には無限に多くの無理数が含まれる。逆もまた真で、すべての無理数の近傍には無限に多くの有理数が存在する。
- 有理数の集合と無理数の集合はどちらも無限集合である。しかし無理数の方が有理数よりももっと数多く存在する。すなわち無限の濃度が高い。
- ピタゴラス教団のシンボルは五角形の中に埋め込まれた5つの頂点をもつ星形である。
- ピタゴラス的生活の重要な点は、道徳的な基礎として哲学および数学の研究を追求したことである。
- 対角線は他の対角線によって1つの長さの異なる比に分割される。この比は黄金分割である。無理数1: 1.618...
- テトラクトゥス:
ピタゴラス教徒は全天空は音階と数であると信じていた。音楽における基本の比は1,2,3,4で、その和は10になる。彼らは テトラクトゥスを神聖なものと考えそれに誓いを立てた。
|
-
>Top Elements of Euclid of Alexandria (c 300 BC):
- The Greeks developed an entire theory of geometry and it is mostly
unchanged, thai is taught in schools today.
- Theorem:
The proof os theorem is a rigorous justification of the veracity
of the theorem in such a way that it cannot be disputed by anyone
who follows the rules of logic, and who accepts a set of axioms.
- Eudoxus of Cnidus (408-355 BC):
He invented a "method of exhaustion," which he used to
find areas of geometric figures by using inscribed figures. This
is equivalent to methods used today in integral calculus.
- Archimedes of Syracuse (287-212 BC):
Archimedes' discovery of the first law of hydrostatics: the law
that a submerged body loses from the weight of the liquid it displaces.
When he discovered the law, he shouted "Eureka!." ( I
found it)
- Diophantus of Alexandria (c AD 250):
He wrote the Arithmetica, which developed algebraic concepts
and gave rise to a certain type of equation. These are the Diophantine
equations used in today. A way of dividing a given square number
into the sum of two squares that inspired Fermat.
- Mohammed Ibn Musa Al-Khowarizmi (c 800):
He wrote 'Al Jabr Wa'l Muqabalah.' (algebra is derived from this),
concerned with straightforwarded solutions of equations of first
and second degree.
- One field that links algebra and geometry: Algebraic geometry
developed in 20C.
- Leonardo of Pisa (1180-1250, Fibonacci, son of
Bonaccio):
He wrote Liber Quadratorum and Liber Abaci. He
is best known for the sequence of numbers: Fibonacci Numbers.
- Each term after the first is obtained adding together the
tow numbers that precede it.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
- The ratio of two successive numbers in the sequence tends
to the Golden Section:
... 34/55, 55/89, 89/144,...(√5+1)/2
- Fibonacci sequence appears everywhere in nature. Leaves on
a branch, the number of petals, Sunflowers,
|
-
ユークリッドの原論 (300 BC頃)
- ギリシャ人は幾何学の全理論を発展させ得た、今日そのほとんどは変わずに、学校で教えられている。
- 定理:
定理の証明とは、その定理の正しさを示す厳密な正当化であり、それは論理学のルールに従い、予め設けられた公理の集合を受け入れた者なら誰も反論できないやり方をとる。
- クニドゥスのエウドクソス (408-355 BC):
取り尽くし法を発見。これは内接する図形を使って幾何学図形の面積を求めた。今日積分で使われている方法である。
- シラクサのアルキメデス (187-212 BC):
彼は 流体力学の第一法則を発見した。これは液体に沈めた物体は、それが押し退けた液体の重さの分だけ軽くなる。この法則を発見したとき、彼はユレーカ
(見つけた) と叫んだ。
- アレキサンドリアのディオファントス (AD 250頃):
彼はArithmetica を書き、代数的概念を発展させ、ある種の方程式を型を提起した。今日ディオファントス方程式として使われている。
与えられえた平方数を2つの平方数の和に分解する方法を求める方法はフェルマーに刺激を与えた。
- ムハンマド・イブン・ムーサ・アルフワーリズミー (800頃) Al Jabr Wa'l Muqabalahを著作
(代数の語源) 。この本は一次および二次方程式の解そのものを扱っている。
- 代数と幾何の両分野を結びつけた分野は代数幾何学で、これは20Cに発展した。
- ピサのレオナルド (1180-1250、フィボナッチ):
Liber QuadratorumとLiber Abaciの著者。彼の名を有名にしているのはフィボナッチ数列である。
- 第二項以降の各項は前2つの項の和。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
- さらに、この数列の隣り合う2項間の比は黄金比に近づく。
... 34/55, 55/89, 89/144,...(√5+1)/2
- フィボナッチ数列は自然に至るところに出現する。枝に生える葉の数、花弁の数、ひまわり...
|
>Top 2. Renaissance quest for ancient knowledge:
- Theorem: is a statement with a proof.
- Conjecture, or Hypothesis: a statement may
be very meaningful and important , but without the proof.
- lemma: it is a preliminary proven statement which then leads
to a more profound theorem.
- Corollaries: proven results that follow a theorem.
- 200 years after Fermat's theorem was only proven correct for the
exponents 3,4,5,6, and 7. I would be a long way to infinity, which
is what one had to do to prove the theorem for any exponent n.
- Leonhard Euler (1707-1783 ):
Euler loved one mathematical formula, which he considered the most
beautiful and put it above the gates of the Academy. The formula
is:
- eiπ+1=0
- The severn bridges of Konigsberg:
Euler asked whether or not it was possible to cross all seven
bridges without passing twice on any bridge. It is impossible.
- Four color map problem:
What would be the minimum number of colors to be used for the
countries colored differently.
- Why did Gauss never try to prove Fermat's Last Theorem? Probably
he knew how deceptive it really was.
- Imaginary numbers:
The complex plane is the smallest field of numbers that contains
the solutions of all quadratic equations. It was found to be very
useful, even in applications in engineering, fluid mechanics,
and other areas.
- Gauss found that analytic functions had special smoothness,
and they allowed for particularly neat calculations. Analytic
functions preserved angles between lines and arcs on the plane.
|
2. 古代の知を探求したルネサンス:
- 定理:証明された主張のこと。
- 予想または仮説:非常に意味があり重要かも知れないが、証明がないもの。
- 補題:予備として証明された主張で、その先にもっと深い定理に導かれる。
- 系:ある定理から証明された結果
- 200年の間に、フェルマーの定理は、べきが3、4、5、6、7のときに正しいことが証明された。すべてのべきnについてこの定理を証明しなければならず、道なお無限に遠しである。
- レオナード・オイラー (1707-1783):
オイラーは一つの数学の公式を愛し、それを最高の美と考えてアカデミーの門に掲げた。それは、
- ケーニヒスベルグの7つの橋:
どの橋も一度しか通らないで7つ全部の橋を渡ることができるか。オイラーの答えは不可能であった。
- 四色問題:
互いに接しているどの国も違う色に塗り分けるためには、最少で何色必要か?
- ガウスはなぜフェルマーの最終定理を解こうとしなかったのか。おそらく彼はそれがどんなに人を惑わすのかを知っていたのかも知れない。
- 虚数:
複素平面 (ガウス平面)は、すべての二次方程式の解を含む最少の数体である。それは、工学、流体力学などの応用において非常に有益であることが分かっている。
- ガウスは、解析関数が特別の滑らかさを持ち、極めて巧妙な計算方法があることを見つけた。解析関数はその平面上の直線と弧の間の角度を保持する。
|
-
>Top Sophie Germain (1776-1831):
- She was one of very few women active in the profession at that time.
She was one of the most important mathematicians to attempt a proof
of Fermat's Last Theorem.
- Peter Gustav Lejeune Dirichlet (1805-1859):
He proved Fermat's Last Theorem for n=5.
- The following progression of numbers: a, a+b, a+2b, a+3b,
a+4b, .. and so on, where the numbers a and b are integers that
have no common divisor other than 1 (such as 2 and 3,or 3 and
5)
- He proved that this progression of numbers contains infinitely
many prime numbers.
- Analysis deals with continuous things; functions on a continuum
of numbers on the line, which seems vera far from the discrete
world of integers and prime numbers - the realm of number theory.
|
-
ソフィー・ジェルマン (1776-1831):
- 彼女は当時は極めて稀な女性数学者の一人であった。彼女はフェルマーの最終定理の証明を試みた最も重要な数学者の一人であった。
- ペーター・グスタフ・ルジェヌ・ディリクレ (1805-1859):
- 以下のような数列がある。
a, a+b, a+2b, a+3b, a+4b, ... ここでaとbは整数であり、1以外の共約数を持たないとする。
(例えば、2と3、あるいは3と5のような数)
- 彼はこの数列が無限に多くの素数を含むことを証明した。
- 解析学は直線上の連続体についての関数という連続量を扱う。それは整数や素数という離散量の世界とは非常にかけ離れている。それこそが数論の王国である。
|
-
>Top Joseph Fourier (1768-1830):
- He discovered that the most functions can be estimated to any degree
of accuracy by the sum of many sine and cosine functions.
- Fourier analysis is a substantial part of numerical
analysis. The Fourier series of sines and cosines is especially
useful in estimating phenomena that are naturally the sum of
periodic elements.
- Extensions of the periodic functions of Fourier to the complex
plane would lead to the discovery of automorphic functions and modular forms - which also had a crucial impact on
Fermat's Last Theorem through the early 20C work of Henri Poincare.
- Ernst Eduard Kummer(1810-1893):
He got closer than anyone else in his time to a general solution
of Fermat's problem. Kummer invented the theory of ideal numbers,
in attempting to prove Fermat's Last Theorem.
- His work with ideal numbers enabled him to prove Fermat's Last
Theorem for a very extensive class of prime numbers as
the exponent n. Thus, he was able to
prove that Fermat's Last Theorem was true for an infinite number
of exponents, namely those that are divisible by "regular"
primes. The only "irregular" prime number less
than 100 are 37, 59, and 67.
|
-
ジョセフ・フーリエ (1768-1830) :
- 彼が発見したのは、ほとんどの関数がサインとコサインの関数の多くにの和によて、いかなる程度の正確さにおいても近似できることである。
- フーリエ解析は数値解析の本質的な部分となっている。サインとコサインのフーリエ級数は、本来周期的要素の和であるような現象を評価する上で特に役に立つ。
- フーリエの周期関数を複素平面に拡張することで、保型関数 (注:ある写像、変換に対して不変な関数)
やモジュラ形式が発見につながった。これはアンリ・ポアンカレの20世紀初頭の仕事を通じてフェルマーの最終的に定理に決定的なインパクトを与えた。
- エルンスト・エドゥアルト・クンマー (1810-1893) 彼は、当時フェルマーの問題の一般解に最も近づいた。彼はフェルマーの最終定理の証明を試みる中で、理想数
(Ideal numbers) *の理論を発明した。
- *注)イデアル:
ある環の部分環において、それの任意の元に環の任意の元を乗じたものが、またその部分環の一つの元となっていうもの。
- 彼は、理想数を使った研究によって、フェルマーの最終定理が正しいことを素数の非常に大きなクラス (注)
類=集合を一般化した概念) を指数 n とする場合について証明できた。そこで彼は、正則な
(注) 複素変数の関数が微分可能な、holomorphicな) 素数で割り切れる数を指数にもつ無限個のケースについて、フェルマーの最終定理が正しいことを証明できた。100未満の非正則素数は、37、59、67
の3つだけである。
|
>Top 3. Geometry without
Euclid:
- Nicolas Ivanovitch Lobachevsky (1793-1856), and Janos Bolyai (1802-1860):
By doing away with Euclid's axiom that two parallel lines never
meet, these two were able independently to formulate a geometrical
universe.
- Evariste Galois (1811-1832):
As a teenager, Galois absorbed the entire theories of algebra and
equations known to accomplished mathematicians of his day, and developed
his own complete system, known today as Galois Theory.
- He sent it to the head of the French Academy of Science, Cauchy,
hoping that he would help him publish the theory. But Cauchy
was arrogant and careless, and Galois's brilliant manuscript
ended up in a trash can, unread.
- He failed to pass the entry exams to the Ecole Polytechnique
He never took notes or wrote things down until he had actual
results. This method concentrated on ideas rather than detail.
- It was a tragedy that an incredibly intelligent young person
would be questioned by much less able examiners who could not
understand his deep ideas.
- While in the Guard, Galois made one last attempt to publish
his mathematical work. He wrote a paper on the general solution
of equations - reorganized as Galois Theory - and sent it to
Simeon-Denis Poisson at the French Academy of Sciences. Poisson
read the paper but determined that it was "incomprehensible."
- As soon as the two became lovers, a royalist came to "save
her honor" and challenged Galois to a duel. But the most
of that last night before the duel, Galois carefully put down
on paper his entire mathematical theory, and sent it to his
friend Auguste Chevalier. At dawn on May 30, 1832, Galois faced
his challenger. and was shot in the stomach. He died the next
morning. He was 20 years old.
- Niels Henrik Abel (1802-1829):
Cauchy's carelessness and arrogance ruined the life of at least
one other brilliant mathematician.
- He proved that no solution was possible for equations of the
fifth degree.
|
3. 非ユークリッド幾何学:
- ニコラス・イワノビッチ・ロバチェフスキー (1793-1856)とヤーノス・ボヤイ (1802-1860) :
二本の平行線は交わらないというユークリッドの公理を捨て去ることで、彼ら二人は独立に幾何学的宇宙を構築した。
- エヴァリスト・ガロア (1811-1832):
10代でガロアは、当時の一流の数学者知られていた代数と方程式のすべての理論を吸収し、今日ガロア理論として知られる、彼自身の完璧な理論を発展させていた。
- 彼はその論文をフランス科学アカデミーのコーシーに送った。コーシーならこの論文を刊行する支援をしてくれると期待していた。しかしコーシーは尊大でかつ不注意であった。そしてガロアの素晴らしい論文は、読まれもせずにくずかごに捨てられてしまった。
- ガロアはエコール・ポリテクニクの受験に失敗した。彼は実際の結果を得るまでノートも取らなければメモもしなかった。この方法は細部の緻密さよりもアイデアに全力を注いた。
- 信じがたいほどの才能を持った若者が、彼の深いアイデアを理解できないような遙かに才能の劣る試験官に質問されたことは悲劇だった。
- 軍にいる間にも、ガロアは時運の数学的業績を刊行するための最後の試みを行っている。方程式の一般的解法 (ガロア理論)を書き、フランス科学アカデミーのシメオン・ドゥニ・ポワソンへ送った。ポワソンはこの論文を読んだが"理解不可能"と判断した。
- 二人は愛し合う仲になるや否や、そこへ王党派の一人の男が現れ、"彼女の名誉を守るために"とガロアに決闘を申し込む。その決闘前夜の大半の時間を使って、ガロアは彼の全数学理論を注意深く書き残し、友人のオーギュスト・シュヴァリエへ送った。1832年5月30日の夜明け、ガロアは決闘の相手と対峙し、そして彼は胃を撃たれた。彼は翌朝死亡した。20歳だった。
- ニールス・ヘンリク・アーベル (1802-1829):
コーシーの不注意と尊大さのために人生を不意にされた天才数学者が少なくとももう一人いる。
- 彼は五次方程式には代数的解法が存在しないことを証明した。
|
>Top 4. Fin de Siecle:
- Henri Poincare (1854-1912):
The concerned teacher had to caution the young genius; "Don't
do so well, please ... try to be more ordinary." Apparently,
French educators had learned something from the misfortunes of Galois
half a century earlier. His teacher was genuinely worried that Poincare
was so brilliant that he might fail those exams.
- He made major contributions to topology, the area stared by
Euler. In 1895, he published Analysis Situs.
- Modular Forms:
Poincare studied periodic functions, such as the sines and consines
of Fourier not on the number line as Fourier had done, but in the
complex plane. He went even further and posited the existence of
functions with a wider array of symmetries.
- These were functions that remained unchanged when the complex
variable z was changed according to
f(z) → f((az+b)/(cz+d))
Here the elements a, b, c, d, arranged as a matrix,
formed an algebraic group.
- Poincare called such weird functions automorphic forms.
He extended them to even more complicated functions, called
modular forms. The modular forms live on the upper half of the
complex plane, and they have a hyperbolic geometry
- An unexpected connection with a doughnut:
1922. Louis J. Mordell discovered a strange connection between the
solutions of algebraic equations and topology. Some of the elements
of topology are surfaces and spaces. The surfaces could be in any
dimension; in two dimensions, or in 3D, or more. Topology is a study
of continuous functions that act on these spaces, and the properties
of the spaces themselves.
- A simple example of such a surface is a sphere: The ball is
3D, but its surface is s 2D object.
- 2D surfaces in 3D space can be classified according to heir genus. The genus is the number of holes in the surface.
a doughnut (torus) has one hole in it. A cup with two handles
has two holes through it.
- A surface of one genus can be transformed by a continuous
function into another surface of the same genus. The only way
to transform a surface of one genus to one of a different genus
is by closing or opening some holes. This cannot be done by
a continuous function, since it will require some ripping or
fusion together, each of which is a mathematical discontinuity.
- Mordel discovered unexpected connection between the number
of holes in the surface of the space of solution of an equation
and whether or not the equation had a finite number or an infinite
number of solutions.
- If the surface of solutions, using complex numbers for greatest
generality, had two or more holes, then the equation had only
finitely many whole-number solutions. Mordell was unable to
prove his discovery. (Mordell's conjecture)
|
4. 世紀末:
- アンリ・ポアンカレ (1854-1912):
心配した教師はこの若い天才に忠告した「そんなにうまくやらないこと。もっと普通にやりなさい。」 フランスの教育者は明らかに半世紀前のガロアの不幸から何かを学んでいた。彼の教師はポアンカレがあまりにも出来過ぎるので、入学試験に失敗するかもしれないと心から心配していた。
- 彼はオイラーが始めたトポロジーの分野に主要な貢献をした。1895年に彼は「位置解析」を出版する。
- モジュラー形式:
ポアンカレはフリーエのサイン、コサインのような周期関数を研究した。但し、フーリエのように数直線上ではなく、複素平面上で考えた。彼は、非常の多くの対称性をもつ関数の存在を想定した。
- 複素変数zが以下の変換に対して不変な関数を考えた。
f(z) → f((az+b)/(cz+d))
ここでa, b, c, d は行列とすれば、代数的な群をつくる。
- ポアンカレはこの奇妙な関数を保型形式と呼んだ。彼は、それらをさらに込み入った関数に拡張し、モジュラー形式と呼んだ。モジュラー形式は複素平面の上半平面に生息し、双曲型幾何学をもつ。
- ドーナツとの予想外の関係:
1922年ルイス・J・モーデルは代数方程式の解とトポロジーとの間に奇妙な関係を発見した。トポロジーの扱うのは曲面や空間である。これらの曲面はどんな次元の中にあってもよい。二次元上でもよいし、三次元空間中あるいはもっと高次元の空間中でもよい。トポロジーはこれらの空間に作用する連続関数、および空間そのものの性質を研究する。
- このような曲面の単純な例は球面である。球は三次元だが、その表面は二次元の対象である。
- 三次元空間における二次元曲面は、その種数に従って分類される。種数とはその曲面に空いている穴の数である。ドーナツ
(トーラス)は穴が1つあり、また取っ手が2つあるカップには穴が2つある。
- ある種数をもつ曲面は、それを連続関数によって変形しても同じ種数をもつ曲面になる。種数を変えるような変形は、穴を閉じるか開けるかによって起こるが、それは連続関数では起こりえない。なぜならそのためには切り取ったり、貼り合わせたりする必要があり、これらの操作は数学的には不連続となる。
- モーデルは、ある方程式の解が作る空間の曲面の穴の数 (種数)と、その方程式が有限個の解を持つか、無限個の解を持つかという問題との間に奇妙な関係を発見した。
- 一般的には複素数で表示される解の曲面は、2つ以上の穴をもつ場合、つまり種数が2以上ならば、その方程式は有限個の整数解しかない。モーデルはこの発見を証明できなかった。
(モーデルの予想)
|
>Top Faltings' Proof:

- In 1983, Gerd Faltings could proved the Mordell conjecture. His
proof had profound implications for the status of FLT . Because
the genus of the Fermat surface for n greater than
3 was 2 or more, it became clear that if integer solutions to the
Fermat equation existed at all, then these were finite.
- Faltings result showed that the number of solutions of Fermat's
equation, if they existed, decreased as the exponent n increased.
The proportion of exponents for which Fermat's Last Theorem
was true approached 100% as increased. In
other words, FLT was almost always true.
- So the status of FLT in 1983 was the following. The theorem
was proven for n up to a million (and in 1992 the limit was
raised to 4 million). In addition, for larger n, if solutions
existed at all then they were very few and decreasing with n.
|
ファルティンクスの証明:
- 1983年にゲルト・ファルティンクスはモーデルの予想を証明した。彼の証明は、フェルマーの最終定理の位置づけにとって深い意味を持っていた。なぜならば指数が3より大きいときは、フェルマー方程式の種数は2以上になるが、その場合もしフェルマー方程式が整数解を持つなら、その個数が有限個でとなる。
- ファルティンクスの結果によって、フェルマー方程式の解の個数は、もし存在するとしたら、指数nが増えるに従って減少する。このことは、フェルマーの定理が正しいための指数の割合は、nの増加に従って100%に近づく。
- 1983までにフェルマーの最終定理の位置づけは、指数が100万まで証明済み。(1992年には400万まで)さらに指数がそれ以上の場合、整数解が存在するとしてもその個数は非常に少なく、かつ指数の増大とともに減少することが判明。
|
>Top 5. Shimura-Taniyama
conjecture:
- Suppose that FLT is not true. Then for some power an
that is greater than 2 there is a solution to Fermat's equation:
X^n + Y^n = Z^n, where X, Y, and Z are integers. This particular
solution, a, b, and c, would then give rise to a specific elliptic
curve.
- The elliptic curve that would arise if FLT were false was
definitely not modular. So, if the Shimura-Taniyama
conjecture was indeed true, then all elliptic curves must be
modular.
- And it would follow that Frey's curve, an elliptic curve that
was not modular could not exit.
- Therefore, the solutions to Fermat's equation could not exit
either. Without the existence of solutions to the Fermat equation,
FLT would be proved.
- What is interesting about FLT is that it spans mathematical history
form the dawn of civilization to our own time. And the theorem's
ultimate solution also spans the breadth of mathematics, involving
fields other than number theory; algebra, analysis, geometry, and
topology - virtually all of mathematics.
|
5. 志村=谷山の予想:
- フェルマーの最終定理が真でないと仮定する。すると2より大きなあるnについて、フェルマーの方程式は少なくとも1組の整数解が存在する。その解a、b、cは、ある特殊な楕円曲線をもたらす。
- フェルマーの最終定理が偽であるという仮定からもたらされる楕円曲線がモジュラーでないということである。ゆえに、もし志村=谷山の予想が真であれば、すべての楕円曲線はモジュラーでなければならない。
- その場合は、フレイ曲線 (モジュラーでない楕円曲線)は存在し得ないことになる。
- 従って、フェルマーの方程式の整数解も存在し得ない。フェルマーの方程式の解の存在が否定されることで、フェルマーの最終定理は証明されることになる。
- フェルマーの最終定理のおもしろさは、この問題が文明の始まりから現代に至る数学の歴史に関わっていることである。そしてこの定理の最終的な解は、数学の広範な分野、数論のほかにも代数、解析、幾何、トポロジーと実質的にすべての数学分野と関連していることにある。
|
>Top 6. Andrew Wiles:
- To prove the Shimura-Taniyama Conjecture, Andrew Wiles knew ha
had to prove that every elliptic curve is modular.
- Wiles realized that the best idea was to try to count the
number of elliptic curves, and to count the number of modular
elliptic curves, and then to show that their number was the
same.
- Wile realized two things. One was that he didn't have to prove
the entire Shimura-Taniyama conjecture, but only a special case;
semistable elliptic curves with rational numbers as the coefficients.
- The other thing was that "counting" would not work
here because he was dealing with infinite sets.
- Fields are large, infinite collections
which are difficult to analyze. Therefore, what number theorists
have often done is to use Galois theory to order to translated these
problems from the complicated fields to what are known as groups.
Often a group is generated by a finite set of elements. Counting
makes sense only for a finite number of elements.
- What Andrew Wiles was trying to do now was to count sets
of Galois representations, corresponding to the (semi-stable)
elliptic curves against the modular forms, and to show that
they are the same.
- The last piece of the puzzle:
In May 1993, Andrew Wiles was getting somewhat frustrated. I seemed
that those few elliptic curves that got away form him were not coming
any nearer. He simply couldn't prove that they were modular.
- To rest a little from his intense search leading nowhere,
Wiles picked up an old paper of the great master Barry Mazur
of Harvard University. Mazur was saying that it was possible
to switch from one set of elliptic curves to another. The switch
had to do with primer numbers. What Mazur was
saying was that if one was dealing with elliptic curves that
were based on the prime number three, it was possible to transform
them to that one could study them using the prime number five
instead.
- This 3-to-5 switch was exactly what Wiles would need. Curves
based on five Wiles had already proved were modular.
- Wiles now used the conventional approach to the presentation
of mathematical results. Instead of doing what he had done in
Cambridge a year and a half earlier, he sent he papers to a
professional journal, the Annals of Mathematics, where thy could
be peer-reviewed by other mathematicians. The review process
took a few months, but no flaws were found this time.
- The May, 1995, issue of the journal
contained Wiles' original Cambridge paper and the correction
by Taylor and Wiles. Fermat's Last Theorem was finally laid
to rest.
|
6. アンドリュー・ワイルズ:
- 志村=谷山予想を証明するためには、アンドリュー・ワイズは、すべての楕円曲線がモジュラーであることを証明しなければならなかった。
- 最善のアイデアは、楕円曲線の個数を数え上げ、一方でモジュラーな楕円曲線の個数を数え、両者の個数が同じであることを示すことであるとワイルズは気づいた。
- ワイルズは2つのことに気づいた。一つは、志村=谷山予想の全部を証明する必要はなく、有理係数の準安定な楕円曲線という特別なケースだけでよいということだった。
- もう一つのことは、扱っているのは無限集合なので数え上げが意味をなさないということだった。
- "体"は大きな無限集合で、その解析は困難である。それゆえ、数論家がしばしば行うことは、ガロア理論を使う方法である。それによって込み入った体から"群"に翻訳される。しばしば群は有限集合の要素からなる。数え上げは有限集合の要素の場合のみ意味をもつ。
- 今やワイルズが解こうとしていることは、モジュラー形式に対する(準安定的な)楕円曲線に関するガロア表現の集合を数え上げ、それらが同じであることを示すことであった。
- パズルの最後の一片:
1933年5月、アンドリュー・ワイルズはいらだっていた。彼の証明から逃れた幾つかの楕円曲線は、少しも近づいてこないように見えた。それらがモジュラーであることをワイルズは全く証明できなかった。
- 行き詰まった集中的な研究から離れて休憩をとるために、ワイルズは偉大な師であるハーバード大学のバリー・メイザーの古い論文を手に取った。メイザー曰く、楕円曲線の一つの集合から別の集合へのスイッチが可能であると。そのスイッチは素数同士でなければならなかった。もし素数3の基にする楕円曲線を扱っているならば、代わりに素数5を使って研究できるようにそれらを変換することができるとメイザーは言っていたのだ。
- この3から5へのスイッチは正にワイルズが必要としているものであった。5を基にした楕円曲線ならば、それらがモジュラーであることをワイルズはすでに証明済だった。
- 今回、ワイルズは数学的成果を発表するのに伝統に従って1年半前にケンブリッジで行ったようなやり方はせず、ワイルズは2つの論文を専門誌アナルスへ送った。それらは他の数学者達による審査に回された。審査には数ヶ月かかったが、今回は何の問題も見つからなかった。
- 1995年5月、ワイルズのケンブリッジ論文とテイラーとワイルズ共著の集成論文とを掲載した数学年報が刊行された。フェルマーの最終定理はようやく安らかな眠りについたのである。
|
>Top 7. A 20th century
proof:
- Andrew Wiles described his proof as a 20C proof. Indeed, Wiled
used the work of many 20C mathematicians. He also used the work
of earlier mathematicians. So the proof of FLT was really the achievement
of a large number of mathematicians.
- According to Wiles, Fermat could not possibly have had this
proof in mind when he wrote his famous note in the margin. This
much is true, because the Simula-Taniyama conjecture did not
exit until 20c. But could Fermat have had another proof in mind?
- The answer is probably not. ut this is not a certainty. We
will never know. On the other hand, Fermat lived another 28
years after the wrote his theorem in the margin. And he never
said anything more about it. Possibly he knew he couldn't prove
the theorem.
- Proving the theorem the way it was finally done in the 1990s required
a lot more mathematics than Fermat himself could have known. The
profound nature of the theorem is that not only does its history
span the length of human civilization, but the final solution of
the problem came about by harnessing - and in a sense unifying -
the entire breadth of mathematics.
- But just because a proof exits and it is a very complicated, advance
one does not mean that a simpler proof is not possible. Ribet, in
fact, points out in one of his papers a direction where a proof
of Fermat's theorem might be possible without a proof of the Shimura-Taniyama
conjecture.
- So whether or not Fermat did possess a "truly marvelous
proof" of his theorem, one that could not fit in the
margin of hi book, will forever remain his secret.
|
7. 20世紀の証明:
- アンドリュー・ワイルズは、自分の証明のことを20世紀の証明と呼んだ。確かに、ワイルズは20Cの数学者達のの成果を利用した。また彼はもっと以前の数学者達の仕事も活用している。
- ワイルズによれば、フェルマーはおそらく余白のその有名なメモを書いたときに、おそらく証明は頭にあり得なかっただろうと言う。むろんそれが真実であろう。20世紀になるまで志村=谷山予想は存在しなかったのだから。
- その答えもおそらく否であるが、確かなことはわからないし、これからも決してわからないだろう。一方、フェルマーは余白に彼の定理を書いた後、28年間も生き、その間にこの問題について、それ以上のことは何も言い残していない。おそらく、彼は自分がこの定理を証明できないと思っていたのであろう。
- 1990年代についに達成されえたこの定理の証明法にはフェルマー自身が知り得たよりも遙かに多くの数学的知識が必要である。この定理の奥深さは、それが人類の文明の長さと同じ位長い歴史をもつだけでなく、この問題の最終解決がすべての数学を利用することによって、それをいわば統一することによって、達成されたという事実に示されている。
- しかし、一つの証明が存在し、それが非常に複雑で高級なものであるという理由だけで、もっと簡単な証明が不可能であるとは言えない。事実、リベットは、彼の論文の中で、志村=谷山予想の証明なしでフェルマーの定理の証明が可能になるかも知れない一つの方向を示している。
- フェルマーが彼の定理の「真に驚くべき証明」をもっていなのか否か、それは蔵書の余白に書くには長すぎただろうが、今では永遠にフェルマーの秘密であり続けるだろう。
|

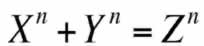



 The
special symbol of the Pythagorean order was the five-pointed star
embedded in a pentagon.
The
special symbol of the Pythagorean order was the five-pointed star
embedded in a pentagon.
 numbers. The basic ratio in music involved only the number
1,2,3, and 4, whose sum is 10. They considered the tetraktys holy
and even swore oaths by it.
numbers. The basic ratio in music involved only the number
1,2,3, and 4, whose sum is 10. They considered the tetraktys holy
and even swore oaths by it.