Résumé |
Remarks |
>Top 0. Nothing Doing:
- The history of zero:
is an ancient one. Its roots stretch back to the dawn to mathematics,
in the time thousands of years before the first civilization. But
as natural as zero seems to us today, for ancient people zero was
a foreign - and frightening - idea.
- The beginning of mathematical thought were found in the need
to keep track of property and of the passage of time. None of
these tasks requires zero; civilizations functioned perfectly
well for millennia before its discovery.
- Stone Age:
Karl Absolom uncovered a 30,000-year-old wolf bone with a series
of notches carved into it.
- South American binary system:
Bacairi and Bororo people of Brazil have number systems that
go "one," "two," "two and one,"
"two and two," and so forth.
- Egypt:
More than 5,000 years ago, the ancient Egyptians designed a
system for transcribing their decimal system, where pictures
stood for number. a single vertical mark represented a unit,
while a heel bone represented 10, a swirly snare stood for 100,
and so on.
- Though counting abilities were rare in the ancient world,
numbers and the fundamentals of counting always developed before
writing and reading.
|
0. 何もしない：
- ゼロの歴史：
ゼロの歴史は古い。その起源は、初期の文明より早く、数学の黎明期である数千年前にさかのぼる。しかし現代人にとってゼロが自然であるが、昔の人にとっては異質で恐怖の思想であった。
- 数学的思考の最初は、資産の記録や時間の経過を知るためだった。このためにはゼロは必要とされなかった。ゼロが発見までの何千年も文明は完全に機能していたのである。
- 石器時代：
Karl Absolomは３万年前の狼の骨に刻印の列を発見した。
- 南米の二進法：
ブラジルのBacairiとBororo族は、1、2、2と1、2と2などのような数字のシステムをもっていた。
- エジプト：
５千年以上前の古代エジプト人は十進法による絵による表記を生み出した。垂直の印は1を、かかとの骨は10を、渦のワナは100を表した。
- 古代における数の表記能力は珍しいことであったにも拘わらず、数は数える基本は常に読み書き以前に発達した。
|
>Top The birth of Zero:
- The Greeks understood mathematics better than the Egyptians did; once they mastered the Egyptian art of geometry, Greek mathematicians
quickly surpassed their teachers.
- Instead of using pictures to represent numbers, the Greeks used letters. H(eta) stood for hekaton: 100. M(mu)
stood for myriori: 10,000 - the myriad. They also had
a symbol for five, indicating a mixed quinary-decimal system.
- Instead of using two strokes to represent 2, or three Hs to
represent 300, a newer Greek system of writing had distinct
letter for 2, 3, 300, and many other numbers. In this way the
Greeks avoided repeated letters. Eg. 87 in the Egyptian system
would require 15 symbols. The new Greek system would need only
two symbols; π for 80, and ζfro 7.
- The Roman system, which supplanted Greek numbers, was
a step backward toward the less sophisticated Egyptian system.
The Roman 87, LXXXVII, requires seven symbols, with several
repeats.
- The Babylonian system seems perverse. The system is
sexagesimal. Also, they used only two marks to represent their
numbers; a wedge that represented 1 and a double wedge that
represented 10. But the really odd feature of the Babylonian
system was that it could represent a multitude of different
numbers. a single wedge could stand for 1; 60; 3,600; or countless
others.
- They had invented machines that helped them count; abacus. (The words calculate come form Latin word for pebble.) Adding numbers on an abacus is as simple as moving the stones
up and down. Each 1 in the number 111 stands for a different
value; from right to left, they stand for one, ten, and
one hundred respectively. A single stone in the first column
is easy to distinguish from a single stone in the second
column. The same isn't true for writing.
- >Top Zero was the solution to the problem. By around 300
BC the Babylonians had started using two slanted
wedges to represent an empty space, an empty column
on the abacus.
- Though zero was useful, it was only a place holder. It
didn't really have a numerical value of its own. Zero was
a digit, not a number. It had no value.
- In the Babylonian system with zero in it, it's easy to
write fractions. They used the numbers 1;30 for $\frac{1}{2}$ and
1;45 for $\frac{3}{4}$.
- Mayan of Mexico:
The Mayans had a number system - and a calendar - that made
more sense than ours does. Like the Babylonians, the Mayans
had a place-value system of digits and places. They had
a vegesimal system.
- The Mayans had a zero in their counting system; The first
day of the month of Zip, was usually called the "installation"
or "seating" of Zip. The next day was 1 Zip, the
following day was 2 Zip, and so forth, until they reached
19 Zip. Each month had 20 days, numbered 0 through 19, not
numbered 1 through 20 as we do today.
|
ゼロの誕生：
- ギリシャ人はエジプト人より数学をよく理解していた。エジプトの幾何学をマスターするや、ギリシャの数学はすぐにその師匠を追い越した。
- 数を表すのに絵の代わりに、ギリシャ人は文字を用いた。H(エタ)は百を、M(ム)は万を表した。また、彼らは５の表記があり、５進法・10進法の混合であった。
- ２を表すのに２回、Hを３回で300を表す代わりに、新たなギリシャの表記法では2、3、300など多くの数字表記を持っていた。例えば87は、エジプトのシステムでは15文字を要したが、ギリシャの新表記では２文字、即ち、80を表すπと7を表すζである。
- ローマのシステムはギリシャを踏襲したが、若干単純なエジプト表記に戻ってしまった。ローマでの87はLXXXVIIとなり、7文字の繰り返しとなる。
- バビロニアのシステムは奇妙に見える。このシステムは20進法である。また彼らは数を表すのに1を1本の楔文字、10を表すのに2本の楔文字を用いた。さらにバビロニアの表記の変わっているところは、同じ表記で異なる数字を表現したことである。一本の楔文字は、1、60、3600などを表した。
- 彼らは計算機である算盤を発明した。(calculateはラテン語で小石の意) 数を算盤で加えることは石を上下に移動させることで簡単にできる。111におけるそれぞれの1は値が異なり、右から左で、1、10、100を表す。最初の桁の石は次の桁と簡単に区別できるが、書くとなると区別は簡単ではない。
- ゼロはこの問題の解決となった。300 BC頃、バビロニア人は空を表す二本の斜めの楔文字を使って、算盤上の何もない空間を表現した。
- ゼロは有用であったが、それは単に場所を示すに過ぎず、それ自身の数としての値をもたなかった。ゼロは桁であって数ではなく、値をもたなかった。
- ゼロを有するバビロニアのシステムでは小数表記が容易である。彼らは1;30で$\frac{1}{2}$を、また1;45で$\frac{3}{4}$を表した。
- マヤ（メキシコ）：
マヤにも数字表記システムと歴があり、それは現在の我々よりも優れていた。バビロニア人のように、マヤ人は位取りの桁の表記システムをもっていた。
- マヤは数を数えるのにゼロがあった。Zipの月の最初に日はZipの設置あるいは台座と呼ばれた。次の日はZip-1、その次はZip-2となり、Zip-19まで続く。一ヶ月は20日あり、それは0日から19日であり、今日の我々のように1日から20日ではない。
|
>Top The fearsome Properties of Nothing:
- It is hard to imagine being afraid of a number. Yet zero was inexorably
linked with the void - with nothing. There was a primal fear of
void and chaos.
- The Greeks claimed that at first darkness was the mother of
all thing, and from darkness sprang Chaos.
- But the fear of zero went deeper than unease about the void.
Unlike the other digits in the Babylonian system, zero never
was allowed to stand alone - for good reason.
- Add a number to itself and it changes. One and one is not
one - it's two. But zero and zero is zero. Zero refused to get
bigger. It also refuses to make any other number bigger. Take
zero away from two and you get two. Zero has no substance. Yet
this substanceless number threatens to undermine the simplest
operations in mathematics, like multiplication and division.
- Strange things also happen when we look at $\frac{1}{0}$ in a different
way. Worst of all, if you wantonly divide by zero, you can destroy
the entire foundation of logic and mathematics.
|
無の性質に対する畏れ：
- 数字を畏れることは想像しがたいが、ゼロは厳然として無の意味と結びつく。無とか混沌とかに対する畏怖の念である。
- ギリシャ人はまずすべての母なる始まりは闇であり、闇から混沌が生まれたとする。
- さらにゼロへの畏怖は無という不安よりも深くなっていった。バビロニアの表記でもゼロは決して単独ではまともには存在していない。
- 数字にそれ自身を加えると変化する。1足す1は1ではなく2となる。だがゼロ足すゼロはゼロである。ゼロは大きくならない。またどの他の数も大きくしない。2からゼロを引くと2である。ゼロには実体がない。この実体のない数字は数学における簡単な掛け算や割り算の操作を傷つける。
- もし$\frac{1}{0}$のような操作をすると変なことがおこる。なお悪いことにきまぐれにゼロで割ろうものなら、すべての論議と数学の根幹が壊れてしまう。
|
>Top 1. Nothing comes of nothing:
- Zero and Western Philosophy:
Zero clashed with one of the central tenets of Western philosophy,
a dictum whose roots were in the number-philosophy of Pythagoras
and whose importance came from the paradoxes of Zeno. The whole
Greek universe rested upon this pillar; there is no void.
- There is no zero. Because of this, the West could not accept
zero for nearly two millennia.
- For everything in the universe to be governed by ratios, as the Pythagoreans hoped. It literally had to be rational.
More precisely, these ratios had to be written in the form $\frac{a}{b}$,
where a and b were nice, neat counting
numbers. (b is not allowed to be zero)
- But the irrational is nestles within the simplicity of the
square. If you draw the diagonal, the irrational appears.
- This meant trouble for the Pythagorean doctrine. Irrationality
was dangerous to Pythagoras, as it threatened the basis of his
ratio-universe. To add insult to injury, they soon discovered
that the golden ratio, the ultimate symbol of beauty and rationality,
was an irrational number. The irrationals were kept secret.
- With Babylonian astronomy came Babylonian numbers. The
Greeks adopted a sexagesimal number system and even divided hours
into 60 minutes, and minutes into 60 seconds. Greek astronomical
tables regularly employed zero; its symbol was the lowercase omicron, o, which looks very much like our modern-day zero.. The Greeks
saw the usefulness of zero in their calculations, yet they still
rejected it. It was philosophy.
|
1. 無から何も生じない：
- ゼロと西洋哲学：
ゼロは西洋哲学の中心教義と衝突する。それはピタゴラスの数哲学の根幹の教義であり、それは重要性はゼノンのパラドックスに由来する。すべてのギリシャ世界では、無はないという柱の上に築かれている。
- ゼロは存在しない。それゆえに西洋は二千年もの間、ゼロを受認しなかった。
- ピタゴラス派は、宇宙のすべては比によって支配されているとした。それは文字通り、合理的(=有理数)でなければならなかった。これらの比は$\frac{a}{b}$の形式に書ければならなかった。ここでa もbもきれいな数えられる数字である。(但し、ｂはゼロは許されない)
- しかし不合理(=無理数)が正四角形の単純さの中に宿っていた。その対角線を引くと無理数が現れる。
- これはピタゴラス派の教義にとっては具合悪かった。無理数はピタゴラス派にとって彼らの比の世界の基礎を揺るがす脅威だった。その不具合をさらに傷つけるものとして、彼らはまもなく美しさと合理性の象徴である黄金比が無理数であることを発見する。無理数は秘密扱いとされた。
- バビロニアの天文学はバビロニアの数字とともなってきた。ギリシャ人は20進法を取り入れ、1時間を60分に、1分を60秒に分割さえした。ギリシャ人は天文表に几帳面にゼロを記載し、その表記は今日の我々のゼロの表記に似ている小文字のオミクロン(ο)であった。ギリシャ人は計算上ゼロの効用はわかっていたが、それでもそれを拒絶した。それが哲学だったのだ。
|
>Top The Infinite, the Void, and the West:
- The infinite and the void had powers that frightened the Greeks.
The infinite threatened to make all motion impossible, while the
void threatened to smash the nutshell universe into a thousand flinders.
- Zeno (born around 490 BC) had a paradox; nothing in
the universe could move. In his most famous puzzle, "The
Achilles", Zeno proves that swift Achilles can never catch
up with a lumbering tortoise that has a head start.
- The Greeks did not have zero, but we do, and it is
the key to solving puzzle.
- Infinity, zero, and the concept of limits are all tied together
in a bundle. Greek philosophers were unable to untie that bundle;
therefore, they were ill-equipped to solve Zeno's puzzle.
- Atomists, other schools of thought:
They believed that the universe is made up of little particles
called atoms, which are indivisible and eternal. Motion was
the movement of these little particles. Of course, for these
atoms to move, there has to be empty space for them to move
into. The atomic theory required that the universe be filled
with emptiness - an infinite vacuum - infinity and zero wrapped
into one. Because atoms are indivisible, there is a point beyond
which things could not be divided. Zeno's hairsplitting doesn't
go on ad infinitum.
- >Top Aristotelian (384 BC):
It turned the universe into a cozy nutshell. There was no infinity,
no void - just beautiful spheres that surrounded the earth,
which was naturally placed at the very center of the universe.
This was later refined by the Alexandrian astronomer Ptolemy
(2C). It became the dominant philosophy in the West.
- The heavenly spheres are slowly spinning in their places.
The stationary earth cannot be the source of that motive
power, so the innermost sphere must be moved by the next
sphere out. That sphere, in turn, is moved by its larger
neighbor, and so and on. However, there is no infinity;
there are a finite number of spheres. Something must be
moving the sphere of fixed stars. This is the prime mover:
God.
- There was a problem, though. It is not so easy to reject
both infinity and zero. Look back through time. There must
be a first event; creation. But what existed before creation?
Void? That was unacceptable to Aristotle.
- Archimedes (born 287 BC in Samos):
was the only thinker of his day to glimpse the infinite. Archimedes
determined whether the crown was pure gold or had been mixed
with lead. He leapt out of the tub and ran through the streets
of Syracuse shouting, "Eureka!." He first glimpse
the infinite in the polish of his war mirrors.
- For centuries the Greeks had been fascinated with conic
sections. Archimedes figured out a way to measure the parabola's
area by resorting to the infinite. The first step was to
inscribe a triangle inside the parabola. He summed the areas
of the infinite triangles and divined the the area of the
parabola.
|
無限、無、そして西洋：
- 無限と無にはギリシャ人を脅かした力がある。無限ははすべての動きを不可能にするし、無は確固たる宇宙を多くの破片に粉砕する畏れがある。
- ゼノン（490 BC頃生まれ）のパラドックスによれば、宇宙のものはすべて動かない。また最も有名なパズルに「アキレスと亀」がある。ゼノンは敏捷なアキレスは、先に出発したのろい亀に決して追いつかないことを証明した。
- ギリシャ人にはゼロがなく、それこそがこのパズルを解く鍵である。
- 無限、ゼロ、そして極限の概念はすべてひとつに結びついている。ギリシャの哲学者のパズルを解くには道具不足だったのである。
- 原子論者、他の思想家：
彼らは宇宙はアトムと呼ばれる微小の粒子からできているとし、それはそれ以上分割できず、その存在は無限であるとした。動きとは、この微粒子の動きである。もちろんこのアトムが動くためには、動くための空間がなければならない。アトム理論によれば、宇宙は空、即ち無限の真空で満たされていなければならず、ここで無限とゼロとは一つになる。アトムは分割できないので、ものごとはこれ以上分割できない点がある。ゼノンの屁理屈は無限に続くことはできない。
- アリストテレス派（384 BC）：
これは宇宙を居心地のよいクルミ殻状と見なした。無限もなく無もなく、ただ美しい球体が宇宙の中心に位置する地球を覆っているとした。この理論は後にアレキサンドリアのトレミー(2C)によって精緻になり、西洋の支配的な哲学となる。
- 天体がゆっくりとそれぞれの場所で回転している。不動の地球にはこれを動かす力はなく、内側の球はその外側の球によって動かされる。この球はさらに外側の大きな球によって動かされる。但し、無限ではなく有限の球があるだけである。何かが不動の星々の球を動かさねばならず、これを動かすのが神である。
- だが問題がある。無限もゼロも否定するのは容易ではない。時間を遡ってみよう。最初の出来事、天地創造があるはずである。だがその創造の前はどうだったのか、無か。そのことはアリストテレスには受け入れ難かった。
- アルキメデス(287 BC Samos生まれ）：
当時無限に触れた唯一の思想家。アルキメデスは王冠が純金が鉛が混入しているかを決定した。バスタブを飛び出し、シラクサの町を
"Eureka!"(findの意)と叫びながら走った。
- 何世紀の間ギリシャ人は円錐曲線に魅了されていた。アルキメデスは放物線の面積を無限によって求積する方法を編み出した。始めは放物線に内接する三角形を描くのである。彼は無限に続く三角形の面積を足し合わせることで放物線の面積を予測した。
|
>Top The Zeroth Number:
- The space shuttle always waits for zero before it blasts into the
air; .... Three, Two, One, Liftoff.
When you drive toward the site where a bomb wet off, you're approaching ground zero. A stopwatch starts ticking from 0:00.00. A car's
odometer comes from the factory set at 00000. The military's day
officially begins at 0000 hours.
- We don't have to worry about mixing up the value of the number
- its cardinality - with the order in which it arrives
- its ordinality - since they are essentially the same
thing. The numbers went 0, 1, 2, 3: zero came first, one was
second in line.
|
ゼロ番目の数字：
- スペースシャトルは常に宇宙に向けての発射にゼロを待っている。3、2、1、発射。
爆心地に向かって運転している車はゼロ地点(Ground Zero)に近づいている。ストップウォッチは0:00.00から刻み始める。自動車の走行距離計は工場出荷時は、00000である。軍の一日は、0000時間から始まる。
- 我々は数の値（基数）とその順番（順序数）とは本質的に同じものとして気にかけなかった。数字は0、1、2、3であって、ゼロが最初であり、1が次に続く。
|
>Top 2. Nothing Ventured:
- Zero and the East:
Though the West was afraid of the void, the East welcomed it. In
Europe, zero was an outcast, but in India and later in the Arab
lands, it flourished.
- In 4C, Alexander the Great marched with his Persian
troops from Babylon to India. It was through this invasion that
Indian mathematicians first learned about the Babylonian system
of numbers, and about zero.
- India was also insulated from Aristotle's philosophy. The
void had an important place in the Hindu religion.
- Like many Eastern religions, Hinduism was steeped in
the symbolism of duality. As with the yin and yang of the Far East and Zoroaster's dualism of good and evil in
the Near East, creation and destruction were intermingled in
Hinduism.
- The god Shiva was both creator and destroyer
of the world and was depicted with the drum of creation
in one hand and a flame of destruction in another. However,
Shiva also represented nothingness. But out of the void,
the universe was born, as was the infinite. Unlike the Western
universe, the Hindu cosmos was infinite in extent; beyond
our own universe were innumerable other universes. Nothingness
was what the world came from, and to achieve nothingness
again became the ultimate goal of mankind.
|
２．虎穴に入らずんば：
- ゼロと東洋：
西洋は無を畏れていたが、東洋はそれを迎え入れた。欧州はゼロを追放したが、インド、後にアラブ世界はそれを歓迎した。
- 4Cに、アレキサンダー大王がペルシャ軍を率いてバビロンからインドまで進軍した。この侵略以降インドの数学者は初めてバビロニアの数体系やゼロについて学んだ。
- インドはアリストテレス哲学の影響を受けなかった。無は、ヒンズー教では重要な位置を占めている。
- 多くの東洋の宗教と同様に、ヒンズー教も二元性の象徴に深く関与している。極東の陰陽や中近東のゾロアスター教の善悪二元論のように、ヒンズー教では創造と破壊とが混在していた。
- シバ神は、世界の創造者であり破壊者であり、片手に創造の太鼓を持ち、もう一方には破壊の炎を持つ。但し、シバ神は無を表している。無からこの宇宙が生まれ、無限も然り。西洋宇宙と異なり、ヒンズー宇宙はその果ては無限であり、我々の宇宙以外にも無数の他の宇宙がある。この世界は無から生じ、そして人類の行き着く先も無である。
|
>Top Zero's Reincarnation:
- Indian mathematicians did more than simply accept zero. They transformed
it, changing its role from mere placeholder to number.
- >Top Around 5C, Indian mathematicians changed their style of numbering;
from Greek-like system to Babylonian-style one. Our numbers
evolved from the symbols that the Indians used; by rights they
should be called Indian numerals rather than Arabic ones.
- The Indians had borrowed little of Greek geometry. Thanks
to their place-number system, they could add and subtract large
numbers in roughly the same way we do today.
- >Top Once number shed their geometric significance, mathematicians
no longer had to worry about mathematical operations making
geometric sense. It was in India (and in China) that negative
numbers first appeared. Brahmagupta (Indian mathematician
in 7C) gave rules for dividing numbers by each other, and he
included the negatives. "Negative divided by negative is
affirmative. Positive divided by negative is negative....",
he wrote.
- However, even the Indians thought that zero was a pretty bizarre
number. Zero multiplied by anything is zero; it sucks everything
into itself. And when you divide with it, all hell breaks loose.
He thought $\frac{0}{0}$ was 0.
- Bhaskara (Indian mathematician in 12C) :
$\frac{1}{0}$ was infinite. "This fraction of which the denominator
is cipher, is termed an infinite quantity."
|
ゼロの再生：
- インドの数学者は単にゼロを受け入れただけではない。彼らは、ゼロを単なる数の代替から役割を変化させた。
- 5C頃、インドの数学者は数の表記方法をギリシャ式からバビロニア式に変えた。我々の数はインド人の表記を踏襲しており、アラビア数字というようりむしろインド数字というべきである。
- 数字が幾何学的な意味から脱すると、数学者はもは数学の計算に幾何的な意味に悩まなくなる。負の数が最初に現れたのはインド(および中国)である。インドの7Cの数学者Brahmaguptaは負の数を含めて、数を相互に割る法則を定めた。負数を負数で割ると正数に、正数を負数で割ると負数に...と。
- しかし、インド人にとってもゼロは奇妙な数であった。ゼロに何を掛けてもゼロであり、ゼロはすべてのものを飲み込んだ。そして、ゼロで割ろうとすると大混乱が起きる。彼は、$\frac{0}{0}$を0と考えた。
- インドの12Cの数学者Bhaskaraは$\frac{1}{0}$は無限大であるとした。「分母はゼロの分数は無限大と定義する」とした。
|
>Top The Arab Numeral:
- By 7C, the West had withered with the fall of Rome, but the East
was flourishing. As the star of the West shank below the horizon,
another star was rising; Islam. Islam would take zero from India
- and the West would eventually take it from Islam.
- In 610 AD, Mohammed fell into a trance on Mount Hira.
- In 632, his followers had captured Egypt, Syria, Mesopotamia,
and Persia.
- By 700, Islam stretched as far as the Indus river and Algiers.
- >Top In 751, they defeated the Chinese Tang dynasty (Battle of Talas). Along the way to China,
the Muslims conquered India. And the Arabs learned about Indian
numerals (as well as paper-making technology).
- The Muslims were quick to absorb the wisdom of the peoples
that they conquered.
- 9C, Caliph al-Mamun founded a great library: the House of
Wisdom at Baghdad, the center of learning in the East like mathematician Mohammed ibn-Musa al-Khowarizmi.
(Algorithm was a corruption of al-Khowarizmi.)
- >Top The Indian name for zero was sunya, meaning
"empty," which the Arabs turned into sifr.
When Western scholars turned sifr into a Latin-sounding
word, zephirus (the root of our word zero).
Other Western mathematicians called zero cifra,
which became cipher. (Cf: French chiffre,
digit)
- Thus, if the Muslims were to accept zero, they had to
reject Aristotle. That was precisely what they did.
- 12C Jewish scholar, Moses Maimonides; noted that instead of
accepting Aristotle's proof of God, the Muslim scholars turned
to the atomists, Aristotle's old rivals.
- The Muslims seized upon the atomists' ideas; now that
zero was around, the void was again a respectable idea.
|
アラブの数字：
- 7Cまでに西洋はローマの陥落によりしぼみ、東洋が興隆しつつあった。西洋の星は地平線に沈み、別の星がのぼってきた。イスラムである。イスラムはゼロをインドから取り入れ、西洋は結果としてイスラムからそれを導入した。
- 610年、モハンムドはHira山で瞑想
- 632年、彼の後継者はエジプト、シリア、メソポタミア、ペルシャを征服
- 751年、唐を破る(タラス湖畔の戦い)。中国への途中でインドを征服。アラブ人はインドの数字と中国から紙の製法を学ぶ。
- ムスリムは征服地での知識吸収に素早かった。
- 9C、カリフのアルマムンは巨大な図書館をバクダッドに建設し、東洋の学問の中心とする。数学者モハメッド・イブン・ムーサ・アルコワリズミを輩出（なお、Algorithm
はこのAl-Khowarizmi がなまったもの）
- インドのゼロのsunyaで空という意味。アラブはそれをsifrと呼んだ。それを西洋の学者はラテン語のzephirusとし、これがzeroの起源となった。他の西洋の数学者はゼロをcifraと呼び、ここからcipherあるいはフランス語ののchiffre (=digit)が生まれた。
- このように、ムスリムがゼロを導入することはアリストテレスを拒絶することであった。事実、彼らはそのようにした。
- 12Cのユダヤ教の学者モーゼス・マイモニデスは書いている。イスラムの学者はアリストテレスの神の証明を受け入れる代わりにその古いライバルである原子論者に組みした、と。
- ムスリムは原子論者の考えを把握し、ゼロを広めた。空の概念は再び尊敬を集めた。
|
>Top Zero's Triumph:
- Christianity initially rejected zero, but trade would soon demand
it.
- 1202, Fibonacci, son of an Italian trader; Imagine
that a farmer has a pair of baby rabbits. Babies take 2 months
to reach maturity, and from then on they produce another pair
of rabbits at the beginning of every month. How many pairs of
rabbits do you have during any given months? The number of rabbits
goes; 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,.... Take any term and
divide it by its previous term: $\frac{8}{5}=1.6, \frac{13}{8}= 1.625, \frac{21}{13}= 1.61538 ...$ These ratios approach the golden ration, which
is 1.61803 ...
- He had learned his mathematics from the Muslims including
zero.
- >Top Germans called the counting board a Rechenbank.
(We call moneylenders banks)
- Italian merchants loved the Arabic numbers. The Arabic
notation was allowed into Italy and soon spread throughout
Europe.
|
ゼロの勝利：
- キリスト教は当初はゼロを拒絶したが、取引がそれを必要とした。
- 1202年、イタリアの商人の息子フィボナッチがいた。
ひとつがいの兎がいると仮定する。兎の子は２ヶ月で成熟し、それから毎月初めにひとつがいの兎を生むとする。ある月数の間に兎のつがい数はいくつになるか。兎の数は
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,となる。どの期間でもその前の期間で割ると、$\frac{8}{5}=1.6, \frac{13}{8}= 1.625, \frac{21}{13}= 1.61538 ...$となる。これらの比率は黄金比(1.61803....)に近づく。
- 彼はムスリムからゼロを含めて数学を学んだ。
- ドイツでは計算板をRechenbankと呼び、これがbankの語源となった。
- イタリアの商人はアラビア数字を好んだ。アラビア表記がイタリアで公認され、まもなるヨーロッパに広がった。
|
>Top 3. The Infinite God of Nothing:
- Zero and Renaissance:
Zero and infinity were at the very center of the renaissance. The
void and the infinite - nothing and everything - would destroy the
Aristotelian foundation of the church and open the way to the scientific
revolution.
- Before 15C, paintings and drawings were largely flat and lifeless.
- >Top Filippo Brunelleschi, an Italian architect, first demonstrated
the power of an infinite zero; he created a realistic painting
by using a vanishing point.
- In 1425, Brunelleschi place just such a point in the center
of a drawing of a famous Florentine building, the Baptistery.
- The vanishing pint has caused most of the universe to
sit in a tiny dot. This is a singularity, a concept
that became very important later in the history of science.
- A contemporary of Brunelleschi, a German cardinal named Nicholas of Cusa, looked at infinity and promptly declared,
"Terra non est centra mundi": the earth
is not the center of the universe. The church didn't yet
realize how dangerous that idea was.
- >Top The power of Copernicus's idea was in its simplicity;
imagined that the sun was at the center, and the planets moved
in simple circles.
- The universe went on into infinity, dotted with innumerable
worlds, each inhabited by mysterious creatures. Were there
other popes on other planets?
- In 1543 Copernicus published his magnum opus on his deathbed.
Copernicus's book, De Revolutionibus, was even dedicated
to Pope Paul III.
- In 1517 a constipated German monk Luther nailed a list
of complaints to the door of the church in Wittenberg.
- In 1580, Giordano Bruno, a former Dominican cleric,
published On the Infinite Universe and World; suggested
that the earth was not the center of the universe and that there
were infinite worlds like our own. In 1600 he was burned at
the stake.
- In 1616 Galileo Galilei was ordered by the church to
cease his scientific investigations. The same year, the book
of Copernicus was placed on the Index of forbidden books.
- Despite the church's Counter-Reformation, the new philosophy
wasn't easily destroyed. It got stronger as time went on. Johannes
Kepler, refined Copernicus's theory, making it even more
accurate than the Ptomemaic system. The planet moved in ellipses
around the sun.
|
３．無という無限の神：
- ゼロとルネッサンス：
ゼロと無限とはルネッサンスの中心的課題である。無と無限は、教会のアリストテレス的な基盤を破壊し、科学革命への道を拓いた。
- 15C以前は、絵画は概して平面で生き生きとしていなかった。
- イタリアの建築家フィリッポ・ブルネレスキは、初めて消失点を使って、リアリスティクな絵画を描いた。
- 1425年に、ブルネレスキは有名なフローレンスの洗礼堂の建物にこの消失点を使って描いた。
- 消失点は宇宙のほとんどを小さな点に集約する。これは特異点であり、後に科学史にとって非常に重要になる。
- ブルネレスキと同世代のドイツの枢機卿であるニコラウス・クザーヌス、無限を見出しすぐに宣言した。「地球は宇宙の中心ならず」と。教会はまだこの思想の危険性に気づいていなかった。
- コペルニクスの考えの源泉はその単純性にある。太陽が中心にあり惑星はその周りに円を描いている。
- 宇宙は無限に広がっており、無数の世界が点在しており、それぞれ不思議な生物が住んでいる。他の惑星には他の教皇がいるのだろうか。
- 1543年、コペルニクスは死の床で彼の大作を発表する。コペルニクスの著書De Revolutionibusは教皇ポール３世にも献上された。
- 1517年、慎重なドイツの牧師ルターがウィッテンブルグのい教会のドア告訴状を張り出す。
- 1580年、ドミニコ修道会の牧師ジョルダーノ・ブルーノは On the Infinite Universe
and Worldを出版し、地球は宇宙の中心でなく、我々同様の世界は無限に存在することを示唆した。1600年に火あぶりの刑に処せられた。
- 1616年にガリレオ・ガリレイは教会から科学探究の中止命令を受けた。同じ年、コペルニクスの本が発禁リストに加えられた。
- 教会の反改革の動きにも拘わらず、新たな哲学は簡単には破壊されず、時が経つにつれてますます強くなっていった。ヨハネス・ケプラーはコペルニクスの理論を進めてトレミーの体系よりもはるかに正確なものにした。惑星は太陽の周りを楕円軌道で回っていると。
|
-
>Top Zero and the Void:
- Zero and the infinite were at the very center of the philosophical
war taking place during 16C and 17C.
- 1596, Rene Descartes would bring zero to the center
of the number line, and he would seek a proof of God in the
void and the infinite. His most lasting legacy was a mathematical
invention - Cartesian coordinates.
- Like the ancients, Descartes assumed that nothing can
be created out of nothing, which means that all ideas -
all philosophies, all notions, all future discoveries -
already exist in people's brains when they are born. Learning
is just the process of uncovering that previously imprinted
code of laws about the workings of the universe.
- Pascal:
Pascal investigated the vacuum - the nature of the void. In
mathematics when Pascal combined probability theory with zero
and with infinity, he found God.
|
-
ゼロと無：
- ゼロと無限とは、16Cおよび17Cを通じて哲学論争の中心テーマであった。
- 1596年、ルネ・デカルトは、ゼロを数線の中心に置き、神を無と無限の中に証明しようとした。彼の遺産は、デカルト座標を発明したことである。
- 古代人同様に、デカルトは無からは何も生まれないとした。それはすべてのアイデア、すべての哲学、概念、将来の発見はすでに生まれた時の大脳の中に存在している。学習とは宇宙の営みについてのすでに刷り込まれたコード体系を発見するプロセスに過ぎない、と。
- パスカル：
パスカルは無の本質である真空を調査した。数学の分野ではパスカルは、確率論をゼロと無限とに結びつけ、神を発見した。
|
>Top 4. Infinite Zeros and Infidel mathematicians:
- The infinite Zeros:
Zero itself is not immune to the bizarre nature of infinity.
- Consider the following series: 1-1+1-1+1-1+1.....
- This series sums to zero. After all,
(1-1)+(1-1)+(1-1)+.... = 0+0+0+... = 0
- But beware! Group the series in a different way:
1+(-1+1)+(-1+1)+(-1+1)+... = 1+0+0+0+... = 1
- The same infinite sum of zeros can equal o and 1 at the same
time.
- An Italian priest, father Guido Grandi, even used this series
to prove that God could create the universe (1) out of nothing
(0).
- Zero and the Mystical Calculus:
The tangent problem and the area problem both ran afoul of the same
difficulties with infinities and zeros. They are both aspects of
calculus, a scientific tool far more powerful than anything ever
seen before.
- Calculus gave scientists a way to express the laws that govern
the motion of the celestial bodies.
|
４．無限のゼロと無神論的数学者：
- 無限のゼロ：
ゼロ自身も無限の奇妙な性質から逃れられない。
- 以下の数列がある。
1-1+1-1+1-1+1......
- この数列の合計は0となる。
(1-1)+(1-1)+(1-1)+.... = 0+0+0+... = 0
- しかし別の組合せでは1となる。
1+(-1+1)+(-1+1)+(-1+1)+... = 1+0+0+0+... = 1
- 同じ無限のゼロの合計が0であり、同時に1となる。
- イタリアの牧師Guido Grandiは、この数列を利用して神が無(0)から宇宙(1)を作ったことを証明しようとした。
- ゼロと神秘的な微積分学：
接戦問題と面積問題はいずれも無限とゼロの難しさが絡んでいる。それらはいずれも微積分の特徴をもっており、それ以前になかった一番強力な科学的な道具となった。
- 微積分によって天体の動きを支配する法則を表現する方法が得られた。
|
>Top Isaac Newton (born in Xmas in 1642) :
- He figured out the tangent to any smooth curve at any point; know
as differentiation. Newton's type of differentiation was based upon fluxions (=derivative) of mathematical expressions that he
called fluents.
- Newton's method of fluxions was very dubious. It relied upon
an illegal mathematical operation, but it had one huge advantage.
It worked. The method of fluxions not only solved the tangent
problem, it also solved the area problem. Finding the area under
a curve (called integration) is nothing more than the reverse
of differentiation.
- The rules of mathematics were build around counting sheep
and surveying property, yet these very rules govern the way
the universe works.
- Newton describes the motion of all objects in the universe: F=ma, where F is
the force on an object and m is its mass, a is acceleration. (ma is an object's momentum)
- Kepler's third law; described the time it takes for
planets to complete an orbit: $\frac{r^3}{t^2}$; r^3/t^2
= k for time t, distance r,
and a constant k.
- In 1662 Robert Boyle; showed that the pressure p inside in a container (volume v) filled by a gas:
pv = k
- In 1676 Robert Hooke: figured out that the force exerted
by a spring, f, multiplied by the distance, x,
was: f = -kx
|
アイザック・ニュートン(1642年Xmasに誕生)
- 彼は、微分法によって曲線のいかなる点での接線を記述した。ニュートンの微分は、流動率(fluxion)と呼んだ変数の導関数に基づいている。
- ニュートンの導関数法は疑わしいものだった。それは不法な数学的操作に依存していたが、非常に有利な点もあった。有用だったのである。導関数法は接線問題を解いただけでなく、面積問題も解いた。曲線の下の面積を求める方法(積分)は微分の逆操作に他ならない。
- 数学の法則は羊や資産を数えることから始まったが、それは宇宙の仕組みを支配する法則にも当てはまるものである。
- ニュートンは宇宙のすべての物体の動きを記述した。F = ma であり、ここで F は物体に作用する力であり、m は質量、a は加速度である。 ma は運動量である。
- ケプラーの第３法則：惑星が周回するときの時間を記述した。 $\frac{r^3}{t^2}=k$
ここで、t は時間、r は距離、k は常数である。
- 1662年、ボイルは、ガスを充填した容器 (容積v) 内の圧力p を記述した。
PV = k
- 1676年、フックはバネと引っ張った距離x とで生じる力f を記述した。
f = -kx
|
>Top 1673-76: Gottfried Wilhelm Leibniz:
- developed calculus, although in a slightly different form. The two
had a correspondence in the 1670s, making it very difficult to establish
how they influenced each other. (Newton came up with the idea first
in 1660s but hid did not publish his work for 20 years.)
- Newton disliked infinitesimals, the little os
in his fluxion equations; infinitely small, smaller than any
positive number you could name, yet still somehow greater than
zero.
- On the other hand, Leibniz reveled in the infinitesimal. He
wrote dx - an infinitesimally tiny little piece
of x.
- These dys and dxs can be manipulated
just like ordinary numbers, which is why modern mathematicians
usually use Leibniz's notation rather than Newton's.
- Even though mathematicians knew that calculus was deeply flawed
- thanks to the mathematics of zero and infinity - they quickly
embraced the new mathematical tools. Nature speaks in differential
equations.
|
1673-76年、ライブニッツ：
- 微積分学をニュートンとは少し違う方法で発展させた。二人は1960年代を通じて交流があり、相互にどう影響を与え合ったかは定かでない。ニュートンはこのアイデアに1660年代に最初に気づいたが、20年間も出版しなかった。
- ニュートンは自分の導関数の中にある無限小 o が嫌いだった。これはどんな正数よりも小さく、それていてゼロよりは若干大きいのである。
- 一方、ライプニッツは無限小が凝っていた。彼は x の無限小として dx と表記した。
- これらのdyや dx はふつうの数字のように扱えるので、現代数学者はニュートンよりライプニッツの記述法を利用している。
- 数学者たちは微積分学にはゼロと無限に関する数学としては不備があることを知っていたが、新たな数学の道具としてすぐ採用した。自然界は微分方程式通りだったのである。
|
>Top The End of Mysticism:
- Colin Maclaurin and Brook Taylor(UK);
discovered how to use calculus to rewrite functions in a totally
different form:
1/(1-x) can be written as $1+x+x^2+x^3+x^4+ ...$
- Jean Le Rond D'Alembert(1717-, an orphan, an excyclopedist):
hatched the idea of limit and solved calculus's problems
with zero.
He rewrote the infinite sum
$1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} +...+ \frac{1}{2^n} + ....$
as the expression
limit (as n goes to ∞) of $1 + \frac{1}{2} + \frac{1}{4} + 1/8 +...+ 1/2^n$
- By putting this limit sign in front of a series, you
separate the process from the goal. In this way you avoid manipulating
infinities and zeros. Just as Achilles' sub-races are each finite,
each partial sum in a limit is finite. Then, after all your
manipulations are complete, you take the limit; your
extrapolate and figure out where the expression is headed.
- Sometimes the limit doesn't exist. Eg, the infinite
sum of +1 and -1 does not have a limit. The value of
the partial sums flips back and forth between 1 and 0; it's
not really heading to a predictable destination.
- limit: It's a small shift in thinking, but it makes
all the difference in the world.
|
神秘主義の終焉：
- マクローリン、テイラー(英)：
微積分を全く別の形式で書き直すことを発見
$\frac{1}{1-x}$ 次のように書き直せる。
$1+x+x^2+x^3+x^4+ ...$
- ダランベール（1717生、孤児、百科全書派）
limitの考えを提唱し、ゼロに関する微積分学の問題を解決。
$1 +\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +...+ \frac{1}{2^n} + ...$
を以下のように表記した。
limit (n → ∞) of $1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} +...+ \frac{1}{2^n}$
- この数列の前のlimit の印は、到達点に至る過程を分割する。こうして無限やゼロの操作を避けることができる。あのアキレウスと亀の問題をサブレースに分割すると有限となり、その部分では有限となる。このように数学的操作はlimitを使うことで完璧になり、その極限の到達点を外挿することができる。
- limitは存在しないこともある。
例：+1と-1の無限の合計には極限がない。部分での合計は1と0の間を繰り返すが、極限の値はわからない。
- limitとは、考え方の小さな変更だが、世界にとって大きな変化である。
|
>Top 5. Infinity's Twin:
- The Imaginary:
Imaginary numbers never appeared in linear equations, but
they began to crop up in quadratic ones.
- Bhaskara (12C); wrote "there is no square root of a negative
number, for a negative number is not a square."
- Descartes thought that these numbers were even worse than
negative numbers; came up with scornful name: imaginary numbers.
- Algebraist loved i. It was wonderful for solving
polynomials.
- $x^2+1$ suddenly splits into $(x+i)(x-i )$
- $x^3-x^2+x-1=(x-1)(x+i)(x-i)
- As early as 16C, mathematicians were using numbers with i included: complex numbers to solve cubic and quartic
polynomials.
- >Top Point and Counterpoint:
- Gerald Desargues (17C French architect):
was an early pioneer of projective geometry. He used the point at
infinity to prove a number of important new theorems.
- Carl Frederick Gauss (1777- German prodigy):
his work on curvature would become a key component of Einstein's
general theory of relativity.
- Cartesian grid: the horizontal axis represents the real part
of the complex number, while the vertical axis the imaginary
part.
- Multiplication and exponentiation in the complex plane became
geometric ideas: This was the second big advance.
|
５．無限の双子：
- 虚数：
虚数は一次方程式は現れないが、二次方程式には突如出現する。
- バスカラ(12C) 曰く、「負数の平方根は存在しない。負数は平方でないからである」
- デカルト：これらは負数より悪い。虚数という軽蔑した名を提唱した。
- 代数学者はi を尊重した。多項式が解けることはすばらしいことであった。
- 16Cには数学者は複素数を利用して、二次あるいは三次の対公式を解いた。
- 点と反点：
- デザルグ（17c、仏の建築家）
射影幾何学の先駆者。重要な多くの定理を証明に無限における点を利用。
- ガウス(1777生、独の神童）
曲率に関する概念は、アインシュタインの一般相対論に基本概念になった。
- デカルト座標：水平軸は複素数の実数部を示し、垂直軸は虚数部を示す。
- 複素数平面における乗法、べき乗法は幾何学的意味がある。これは次の大きな飛躍となった。
|
>Top 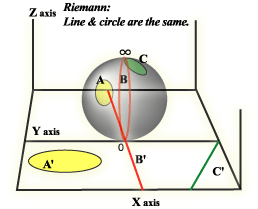 Georg Griedrich Bernhard Riemann (a student of Gauss):
- Riemann imagined a translucent ball siting atop the complex
plane, with the south pole of the ball touching zero. If there were
a tiny light at the north pole of the ball, any figures that are
marked on the ball would cast shadows on the plane below. The shadow
of the equator would be a circle around the origin. Every point
on the ball has a shadow on the complex plane. Every circle on the
plane is the shadow of a circle on the ball, and a circle on the
ball corresponds to a circle on the plane .... with one exception.
a circle that goes through the north pole of the ball, the shadow
is a line. The north pole is like the point at infinity.
- Multiplying by the number of i was equivalent
to spinning the sphere 90 degrees clockwise.
- If you take a number x and replace it with its reciprocal $\frac{1}{x}$, that is equivalent to flipping the sphere upside
down and reflecting it in a mirror. The north pole becomes the
south pole... and zero becomes infinity and infinity becomes
zero. Infinity and zero are simply opposite poles on
the Riemann sphere. And they have equal and opposite powers.
- Choose $\frac{i}{2}$. Square it. Cube it. Raise
it to the fourth power. The fifth. The sixth. The seventh. It
slowly spirals toward zero like water down a drain. What happens
to 2i? That exact opposite. It spirals
outward. But on the number sphere, the two curves are duplicates
of each other; they are mirror images.
- The only numbers that escape are the ones that are equally
distant from the two rivals - the numbers on the equator, like 1, -1, and i. these numbers, pulled
by the tug of both zero and infinity, spiral around on the equator
forever and ever.
|
リーマン（ガウスの弟子）
- リーマンは複素数平面上に乗る透明な球体を想定した。その球の南極はゼロに接している。小さな光が球の北極にあるとすると、球上の図は下の平面に投影する。赤道の陰は円となる。平面上のいかなる円も球場に円の影を描く。また球上の円は平面の円に対応する。但し、例外として、北極を通る円は、平面上では直線となる。北極は無限の点のようになる。
- i を掛けることは、球を時計回りに90度回転させることに相当する。
- もしxの数字に対して、その逆数の$\frac{1}{x}を置くと、それは球を逆さまにした鏡像になる。北極は南極になる。ゼロは無限点に、無限点はゼロになる。リーマン球の上ではゼロと無限点とは対局に位置する。
- $\frac{i}{2}$を選んで、それを2乗、3乗、4乗、5乗、6乗、7乗してみる。それはゆっくりとゼロに向かって水が流れ落ちるように渦を巻いて行く。では 2i ではどうなるか。それは全く反対の方向に渦巻いて行く。しかし数字の平面上ではそれらは全く同じ鏡像関係になる。
- 両極から等距離にある赤道上にある数字だけ（1, -1 や i）がこのようにはならない。これらはゼロと無限点によって引っ張られ、永久に赤道上を回るのである。
|
-
>Top The Infinite Zero:
- Infinity was not longer mystical; it became an ordinary number.
- Georg Cantor (The master anatomist of the infinite, born
in Russia in 1845) :
- Consider the set of whole numbers: {0, 1, 2, 3, .....}
We can remove an infinite number of elements from the set of
whole numbers - we can delete the odd numbers, for example -
and the size of the set remains unchanged. This is the definition
of the infinite. The even numbers, the odd numbers, the whole
numbers, the integers - all of these sets were the same size
(Cantor soon dubbed  0 (Aleph nought).
- >Top Cantor discovered that the set of real numbers is much, much
bigger than the rationals.
Every real number has a seat, and every seat is filled. That
means we can make a list of seats, showing a seat's number along
with the real number that is sitting in it. The trick came when
Cantor created a real number that was not on the list... Going
down the diagonal method ..., we can create a new number.
The perfect seating list cannot exist. The real numbers are
a bigger infinity than the rational numbers. The term for this
type of infinity was 1 (Aleph-one). The term for the infinity of the real line
was C, or the continuum infinity.
- In Cantor's mind there were an infinite number of infinities
- the transfinit numbers - each nested in the other. 0 is smaller than 1,
which is small than 2,
which is smaller than 3,
and so forth.
- Leopold Kronecker launched vitriolic attacks against Cantor's
work and made it extremely difficult for him to publish
papers. But Cantor's work was the foundation of a whole
new branch of mathematics; set theory.
- David Hilbert; says "No one shall expel us
from the paradise which Cantor has created for us."
|
-
無限のゼロ：
- 無限はもはや神秘的ではない。それは普通の数字になった。
- カントール(無限の解剖学者。1845年、ロシア生まれ)
- すべての自然数の集合を考える
{0, 1, 2, 3, .....}
この集合から無限の数の要素を取り除くすることができる。例えば奇数をのぞくいても集合のサイズは変わらない。これが無限の定義である。偶数、奇数、自然数、整数、これらすべの集合は同じ大きさである。カントールはこれを0 (アレフ０)と呼んだ。
- カントールは実数の集合が有理数よりも遙かに大きいことを発見した。
すべｔの実数に席があり、どの席も満席とする。これによって席のリストを作り、そこに位置している実数に沿って席の番号を示すことをできる。カントールの手品は、このリストにない実数を創り出した。それが対角線論法であって、新たな数字を創り出すことができる。つまり完全な席のリストはないことになる。実数は有理数よりも大きな無限だったのである。このタイプの無限を
1 (アレフ１)と呼んだ。この実数の集合をC（連続体無限）という。
- カントールの心中には無限の無限、即ち超限数があった。それぞれがネスト構造をしている。
0 は、1より小さく、それは2より小さく、またそれは3より小さいというように。
- クロネッカーは、カントールの仕事に対し辛辣な反論を行い、彼が出版することを非常に困難にした。しかしカントールの仕事は集合論という新たな数学の領域の基礎になった。
- ヒルベルト曰く「カントールが我々に創ってくれたパラダイスから誰も追放することはできない」
|
-
>Top Cover the stain by a rectangular carpet:
- The number 2.5 is covered by a carpet size between 2 and 3.
As Cantor showed, we can count them off one by one, in order,
based on their seat number. Take the first rational number and
imagine it on the number line. Let's cover it with a carpet
of size 1. Now take the second number. Cover it with a carpet
of size $\frac{1}{2}$. Take the third number and cover it with a carpet
of size$\frac{1}{4}$, and so forth. Go on and on to infinity; since every
rational number is on the seating chart, every rational number
will eventually be covered by a carpet. What is the total size
of the carpets? $1+\frac{1}{2}+\frac{1}{4}+ ... +\frac{1}{2^n}$ goes to 2 as n goes to infinity. So we can cover the infinite cohorts or rational
numbers in the number line with a set of carpets, and the total
size of it is 2. This means that the rational numbers take up
less than two units of space.
We can cover the rationals with carpets that fit in the size
of half an atom or as small as we can possibly imagine.
How big are the rational numbers, then? They take up no space
at all. It's a tough concept to swallow, but it's true ....
- The infinity of the rationals is nothing more than a zero.
|
-
シミを四角のカーペットで覆う：
- 2.5の数字は2と3の間のサイズのカーペットで覆われる。カントールが示したように、それらを一つ一つ、順番に、席の番号によって数えることがことができる。まず数線に乗っている最初の有理数を考える。それをサイズ１のカーペットで覆う。２番目の数字をサイズ$\frac{1}{2}$のカーペットで覆う。３番目の数字をサイズ$\frac{1}{4}$のカーペットで覆い、以下同様とする。これは無限に続く。どの有理数も席の表に乗っており、どの有理数も結局はカーペットに覆われるからである。カーペットの全面積は$1+\frac{1}{2}+\frac{1}{4} + ... +\frac{1}{2^n} $となり、nが極限になると2に近づく。こうして我々は数線上にある無限の集合の有理数をサイズ2のカーペットで覆うことができる。このことは有理数は2つの空間より小さいことを示している。我々は有理数を原子の半分の大きさ、いやいくらでも小さなサイズのカーペットで覆うことができる。では有理数はどの位大きいのだろうか。それはスペースがないのだ。これは理解しがたいが、事実なのだ。
- 有理数の無限性はゼロに他ならないことになる。
|
-
>Top 6. Absolute Zeros:
- For physicists, zero and infinity seemed utter irrelevant to the
workings of the universe. Or so scientists had hoped.
- Zero Heat:
- 1787: Jacque-Alexandre Charles (French physicist):
Charles' law describes the relationship of the volume of a gas
to its temperature.
- 1850s: William Thomson (British physicist):
- A gas cannot keep getting colder and colder indefinitely; this
is absolute zero.
- Kelvin's discovery of absolute zero told physicists
what they couldn't do. But it was the beginning of a new
branch of physics; thermodynamics.
- The nature of light was a problem. Isaac Newton believed that
light was composed of little particles.
- In 1801, a British scientist discovered that light interferes
with itself.
- Stefan-Bolzmann equation; seems to tie the wiggles
of molecules to the wiggles of light. It related the temperature
of an object to the total amount of light energy it radiates.
(The radiated energy is proportional to the temperature
raised to the fourth power.)
- Rayleigh-Jeans law; predicted that an object gives
off more light at smaller wavelength. Consequently at realms
close to zero wavelength, the object gives off an infinite
amount of high-energy light.
- "Ultraviolet catastrophe":
Every object is constantly radiating an infinite amount
of energy, no matter what its temperature is. Zero wavelength
equals infinite energy. Solving this paradox quickly became
the leading puzzle in physics.
|
６．絶対ゼロ：
- 物理学者はゼロと無限とは宇宙の営みにとって無関係に見えた。物理学者はそう希望していた。
- ゼロの熱：
- 1787年：シャルル（仏、物理学者）
シャルルの法則はガスの体積と温度の関係を記述
- 1850年：トムソン（英、物理学者）
ガスは無限に冷やすことはできない。これが絶対零度である。
- 絶対零度を発見したケルビンは、物理学者にこれ以上不可能なことを示した。それが新たな物理学の分野、熱力学の誕生である。
- 光の性質は問題であった。ニュートンは光は小さな粒子からなっていると信じていた。
- 1801年、英の科学者は光がそれ自身で干渉することを発見した。
- ステファン・ボルツマンの式：
分子の振動と光の振動を関係づけた。それは物体の温度とそれが放射する光エネルギー総量を関係づけた。(黒体の総放射エネルギーは絶対温度の4 乗に比例する)
- レイリー・ジーンズの法則：物体は 周波数が小さいほど多くの光を発する。従ってゼロの周波数の領域では物体は無限の高エネルギーを発する。
- 紫外発散：
どの物体も温度の如何を問わず、常に無限量のエネルギーを放射している。ゼロの周波数は無限のエネルギーに等しい。このパラドックスを解くことは先進的な物理学の重要な課題となった。
|
-
>Top Quantum Zero: Infinite Energy:
- Quantum mechanics got rid of the zero in the classical theory of
light.
- 1900: Max Planck's formula:
Molecules are forbidden to move in most ways. They vibrate only
with certain acceptable energies, called quanta. It is impossible
for molecules to have energies in between these acceptable values.
- 1905: Albert Einstein: showed that nature worked in
quanta rather than in smooth increments. He would later become
the chief opponent of the theory he helped create. ("God
does not play dice with the universe.")
- >Top Awarded Nobel Prize by the paper of "Photoelectric
effect." Einstein's idea was that light is quantized
into photons, directly contradicting the wave theory of
light. Indeed, it turns out that light has both a wave nature
and a particle nature.
- 1927: Werner Heisenberg; Uncertainty principle
we cannot measure a particle's position and its momentum with
perfect accuracy at the same time... You can never know both
at the same time, and if you have some information about one,
you must have some uncertainty about the other.
- 1948: Hendrick B.G. Casimir & Dik Polder (Dutch):
They studied the forces between atoms when they realized that
their measurements didn't match the forces that had been predicted.
Casimir realized that the forbidden particle waves would affect
the zero-point energy of the vacuum.
- If you put two metal plates close together and some of
those particles aren't allowed between the plates, then
there are more particles on the outside of the plates than
on the inside. The plates are crushed together, even in
the deepest vacuum. This is the force of the vacuum. This
is the Casimir effect.
|
-
量子的ゼロ、無限のエネルギー：
- 1900年：マックス・プランクの放射法則
分子はほとんどの場合動くことを禁じられている。それらは量子という一定のエネルギーによってのみ振動できる。分子がその中間の値のエネルギーを持つことは不可能である。
- 1905年：アインシュタイン
自然界は連続的な変化ではなく量子によって動いていることを示した。後にかれは自分が援助したこの理論の中心的な反論者になる。「神は宇宙を賭けてサイコロは振らない」と。
- 光電効果の論文によりノーベル賞受賞。アインシュタインのアイデアは、光は量子化されて光子となっており、これは光は波である説と正面から矛盾する。事実、光は波の性質と粒子の性質の両方を持つことが判明した。
- 1927年：ハイゼンベルグの不確定性原理
我々は粒子の位置座標と運動量を同時に正確に測定できる。この二つの情報を同時に知ることはできないということは、一つの情報を知ることはもう一つの情報が不確定になることを意味する。
- 1948年：カシミア＆ポールダー：
彼らが原子間の力を研究していた際その力は予測値と合わなかった。カシミアは、許されない粒子の波が真空でのゼロ点エネルギーの効果であることを示した。
- ２枚の金属版を近づけて、一部の粒子がその金属板の内側に存在できないとすると、外側には内側より多くの粒子があることになる。この金属板は、真空中にもかかわらずクラッシュしたのである。これが真空の力を示すカシミア効果である。
|
>Top 7. The Relativistic Zero: The Black Hole
- Black Hole:
A zero in the other great modern theory - relativity - creates another
paradox: the infinite nothing of the black hole.
- 1887: Albert Michelson & Edward Morley (US) tried to
measure the speed of light should depend on whether you are running
toward or away. They found no difference.
- 1905: Again Albert Einstein:
- The first assumption: Einstein stated that if a number of
people watch the same phenomenon, the laws of physics are the
same for each observer. Here, each observer can't feel an acceleration.
(The principle of relativity)
- The second assumption: Einstein assumed that everybody agrees
about the speed of light in a vacuum: about 300M m/sec (constant c)
- As objects speed up, they get shorter and heavier. At
$\franc{9}{10}$ of the speed of light, a yardstick would one be 0.44
yards long, and one-pound bag would weigh nearly 2.3 pounds.
- >Top The speed of light is the ultimate speed limit; you cannot
reach it, much less exceed it. Nature has defended itself from
an unruly zero.
- It's difficult concept to grasp, but the easiest way to approach
space-time is through an analogy: space and time are like a
gigantic rubber sheet. Planets, stars, and everything else sit
on that sheet, distorting it slightly. That distortion is gravity.
The more massive the object that is sitting on the sheet, the
more the sheet gets distorted, and the larger dimple around
that object.
- Just as space gets distorted close to a massive object,
time does, too. It get slower and slower as the curvature
gets greater and greater. The same thing happens with mass.
As you get into greatly curved regions of space, bodies'
mass effectively increase, a phenomenon known as mass
inflation.
- Einstein's equations also predicted something much more
sinister; the black hole, a star so dense that nothing
can escape its grasp, not even light.
- >Top In 1933, Subrahmanyan Chandrasekhar showed that
a collapsing star that has about 1.4 times the mass of the
sun will have enough gravity to overwhelm the Pauli exclusion
principle. (No two electrons of the same
quantum state can be forced into the same spot.)
- The pressure of the resulting neutrons can stave off collapse
for a light while: neutron star. Every teaspoon weighs
hundreds of million of tons. Some astrophysicists believe
that a little more squeezing makes the neutrons break down
into their component quarks, creating a quark star.
- The curvature goes off to infinity because the black
hole takes up zero space. The zero of a black hole is
a singularity, an open wound in the fabric of the universe.
- A wormhole is a paradox caused by a zero in the equations
of general relativity. Nobody truly know whether or
not wormholes exist.
|
７．相対論的ゼロ：ブラックホール
- ブラックホール：
もうひとつの現代理論である相対性理論は、ゼロについて別のパラドックスを創り出した。ブラックホールという無限の無である。
- 1887年：マイケルソン＆モーリー(米)は、光速が、観測者の動きに依存するかどうかを測定。結果は、変化なし。
- 1905年：再び、アインシュタイン：
- 第一の想定：アインシュタインは同じ現象を大勢の人が観察する場合、物理法則は個々の観察者にとって同じである。但し、各観察者は加速度運動はしていない。(相対論の原理)
- 第二の想定：アインシュタインは誰にとっても真空中の光速は一定である。３億m/sec (常数c）
- 物体が速度を上げると、その長さは短縮し、その重さは増える。光速の$\franc{9}{10}$では、1ヤードの棒は0.44ヤードになり、１ポンドの袋は、2.3ポンドになる。
- 光速は究極の速度制限である。そこに到達することもできないし、ましてそれを越すこともできない。自然は手に負えないゼロから防御している。
- この概念は把握し難い。時空間を比喩によって理解するのがわかりやすい。空間と時間は巨大なゴム膜のようであって、惑星、恒星などすべてのものがこのゴム膜の上にあり、少しゴム膜をゆがめる。そののゆがみが重力である。ゴム膜の上に乗っているより重たい物体は、膜をより大きくゆがませ、そうして大きな凹みが物体の周りにできる。
- 空間が巨大な物体の近くでゆがむのと同様に、時間もゆがむ。ゆがみが大きくなればなるほど、時間はゆっくり進む。同じことが質量にも起こる。空間の大きなゆがみの所では、物体の質量は増加する。質量インフレーションの現象である。
- アインシュタインの式は、もっと不吉なことを予測した。ブラックホールである。それは星の密度が高まると、光さえもそこから逃れられなくなる。
- 1933、チャンドラセカールは、太陽の1.4倍の質量の星が崩壊するときパウリの排他原理(1つの電子状態には１つの電子しか入れない) を凌駕することを示した。
- その結果、中性子の圧力なしばらくの間、崩壊をくい止められ、中性子星となる。これは茶さじ一杯が何億トンという重さになる。一部の天文物理学者は中性子をもう少し圧縮すると、その構成要素のクォークにまで崩壊し、クォーク星となると予測している。
- ブラックホールでは空間がゼロになるので、空間のゆがみが無限大なる。ブラックホールのゼロは特異点であり、宇宙の構造の裂け目である。
- ワームホールは、相対性理論の式のゼロによって創られるパラドックスである。ワームホールが存在するかどうかは誰も本当のことはわからない。
|
>Top 8. Zero Banished: String Theory
- Zero Hour at Ground Zero:
Zero dwells at the juxtaposition of quantum mechanics and relativity;
zero lives where the two theories meet, and zero caused the two
theories to clash. A black hole is a zero in the equations of general
relativity; the energy of the vacuum is a zero in the mathematics
of quantum theory; The big bang, zero in both theories.
- The universe of general relativity is a smooth rubber sheet. Quantum
mechanics describes a jerky and discontinuous universe.
- Just as zero punches a hole in the smooth sheet of general
relativity, zero smooths and spreads out the sharp point charge
of the electron, covering it in a fog. However, since quantum
mechanics deals with zero-dimensional particle-points such as
the electron, technically all particle-particle interactions
in quantum theory deal with infinities; there are singularities.
When two particle merge, they meet at a point; a zero-dimensional
singularity. This singularity makes no sense in quantum mechanics
or in general relativity.
|
８．ゼロの追放：ひも理論
- グランド・ゼロにおけるゼロ時間：
ゼロは量子力学と相対論の並列する所に住んでいる。ゼロは2つの理論が出会うことにあり、そしてゼロはこの２つの理論が崩壊させる。ブラックホールは相対論の式におけるゼロであり、量子論の数学においては、真空のエネルギーはゼロとなる。ビックバンは2つの理論におけるゼロである。
- 相対論の宇宙は滑らかなゴム膜の宇宙である。量子力学はぎくしゃくした不連続な宇宙である。
- ゼロは相対論におけるスムーズな膜に穴をあけるように、ゼロは電子の尖った電荷をスムーズにして霧で覆い隠す。しかし、量子力学は電子を、無限を扱う量子理論における粒子同士の相互作用のように、ゼロ次元の粒子点として取り扱う。これらには特異点が存在する。2つの粒子が合体すると、それらは点で衝突する。これがゼロ次元の特異点である。この特異点は量子力学や相対論では意味をもたない。
|
-
>Top String theory:
- created in
1970s when physicists began to see the advantage of treating every
particle as a vibration string rather than as a dot. If electrons
(and black holes) are treated as one-dimensional, like a loop of
string, instead of as zero-dimensional, like a point, the infinities
in general relativity and quantum mechanics miraculously disappear.
- If the electron is a loop of string, the particle is no longer
a singularity. This means that the mass and charge don't go
off to infinity. Furthermore, as two particles merge, no longer
do they meet at a point like singularity; they form a nice,
smooth, continuous surface in space-time.
- In string theory different particles are really the same type
of string, just wiggling in different ways. Everything in the
universe is made up of these string, which are about 10^-33
cm across; comparing the size of a string to the size of a neutron
is like comparing the size of a neutron to the size of our solar
system.
- Distances (and times) smaller than the size of the loops no
longer matter; they don't make any physical sense. In string
theory, zero has been banished from the universe; there is no
such thing as zero distance or zero time. This solves all the
infinity problems of quantum mechanics.
- >Top String theory would unify quantum mechanics with relativity; it
would lead to the theory of quantum gravity - the Theory of Everything
that explains every phenomenon in the universe. (Grand
Unified Theory, GUT) However, string theory required 10 dimensions to work. The other 6 dimensions are rolled
up like little balls, too tiny to see. What do these six extra dimensions
mean? They don't measure anything that we are accustomed to. They
are simply mathematical constructs that make the mathematical operations
in string theory work in the manner that they have to.
- >Top Scientists now believe that there is a monster theory that
underlies all of these competing theories; the so-called M-theory, which lives in 11 dimensions, not 10.
- For the foreseeable future, banishing zero from the universe
with string theory is a philosophical idea rather than a scientific
one. String theory might well be correct, but we may never have
the means to find out. Zero has not yet been banished; indeed,
zero seems to be what created the cosmos.
|
-
ひも理論：
- 1970年代に物理学者はすべての粒子が点というよう振動するひもとして扱う有利な結論を導き出した。もし電子（やブラックホール）が点のようなゼロ次元でなく、ひものループのような１次元で扱われるとすると、一般相対論や量子力学での無限が不思議と消えていく。
- もし電子が電子がループ状のひもとすると、粒子はもはや特異点ではなくなる。これは質量や電荷が無限大にならないことを意味する。さらに２つの粒子が合体するとき、それらは特異点のような点で出会う必要はなくなり、時空間の中でスムーズで連続的な表面をもつ。
- ひも理論では、異なる粒子は実は同じタイプのひもであり、ただその絡み方が異なる。宇宙のすべてのものはこれらのひもからなり、その大きさは10のマイナス33乗cmである。このヒモを中性子の大きさと比べると、中性子を太陽系の大きさと比べることに匹敵する。
- このループのサイズより小さな距離（や時間）は物理的な意味を持たない。ひも理論では、ゼロは宇宙から消え去り、ゼロの距離もゼロの時間もなくなる。これは量子力学における無限問題を解決する。
- ひも理論は、量子力学と相対論を統一するように見える。それは量子重力理論、つまり宇宙におけるすべての現象を説明する大統一理論（GUT）に通じる。但し、ひも理論では10次元を必要とする。他の6次元は小さなボールのように丸まっていて、あまり小さくて見えない。この追加の6次元はどのような意味があるのか。それは我々が慣れているようなものを測る尺度ではない。それらはひも理論が機能するような数学的操作がもたらした概念に過ぎない。
- 科学者は、これらのさまざまな理論の根底に巨大ないわゆるＭ理論が存在しており、しかもそれは10次元ではなく11次元であろうとしている。
- 考えられる未来においては、ひも理論によって宇宙からゼロを消し去ることは科学的というようり哲学的な考えといえる。ひも理論はかなり正しいかも知れないが、我々はそれを見つけ出す手段を持ち得ないかもしれない。その場合ゼロはなお消し去れないことになる。事実、ゼロがこの宇宙を創り出しているように見える。
|
- >Top 1997: astronomers used supernovas to measure the distance to some
very dim and ancient galaxies. The distance of the galaxy yields
its age and its Doppler shift yields its velocity. The answer they
got was an odd one. The expansion of the universe isn't slowing
down. It might even be speeding up. There is little chance of a
big crunch, because something is opposing the force of gravity.
Once again physicists are talking about the cosmological constant - the mysterious term that Einstein added to his equations to balance
the push of gravity. Einstein's biggest blunder might not have been
a blunder after all. The mysterious force might be the force of
the vacuum.
- The cosmos will expand forever. The universe will die a cold
death, not a hot one.
- The cosmos was spawned from nothing, and will return to the
nothing from whence it came. The universe begins and ends with
zero.
|
- 1997年、天文学者は超新星を使って非常に暗くて遠い銀河までの距離を測定した。銀河までの距離でその年齢がわかり、そのドップラー効果で速度がわかる。その結果、得られた答は奇妙なものだった。宇宙の膨張は減速しておらず、むしろ加速しているのだ。ビッグクランチが起こる可能性はほとんどなくなった。これは重力に反する何かの力があることになる。再び、物理学者は宇宙項(宇宙定数)について議論し始めた。これはアインシュタインが重力方程式の中に重力とバランスとるように加えた不思議な条件である。アインシュタインの最大の誤りとされたが、結局謝りではなかったかもしれないのだ。この不思議な力（万有斥力）は真空エネルギー対応する。
- 宇宙は永遠に膨張すると見られる。宇宙は熱力学的な死ではなくコールドな死を迎えるのだろうか。
- 宇宙は無から誕生し、また生まれたときのように無に帰っていく。宇宙は始まりと終わりもゼロになるのである。
|
